Hemos estudiado ya en entradas anteriores la media aritmética de los divisores y la cuadrática. La geométrica tiene menos interés y no la hemos tratado. Tocaría ahora el turno a la media armónica y, después, a la contraarmónica.
El estudio de la media armónica nos lleva, en primer lugar, a los números de Ore, ya tratados por el autor en https://hojaynumeros.blogspot.com/2010/11/numeros-de-ore.html
Un
número entero positivo N se llama de Ore
o armónico cuando la media armónica
de todos sus divisores es un número entero. Por ejemplo, es armónico 140,
porque sus 12 divisores son 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70 y 140 y por
tanto su media armónica es
Parece
muy pesado este cálculo para números grandes, pero existe una simplificación.
Para ello basta observar que cada divisor d posee un complementario d’
tales que d.d’=N. Este hecho permite ir sustituyendo cada cociente del
tipo 1/d por d’/N, con lo que todos los denominadores resultará iguales a N y
se podrán sumar los cocientes con facilidad:
Este procedimiento es fácilmente generalizable: basta multiplicar N por su número de divisores y dividir después entre la suma de los mismos:
Representamos el número de divisores mediante d(N) y su suma por σ(N), o bien como TAU y SIGMA respectivamente. Basta observar la fórmula para poder interpretarla de otra manera: La media armónica de los divisores equivale al cociente entre el número y la media aritmética de dichos divisores. Podríamos afirmar entonces que la media aritmética de los divisores es otro divisor. Por eso aparecieron números de Ore cuando estudiamos ese caso en los aritméticos.
Este
cambio nos permite calcular la media armónica mediante un sencillo algoritmo:
Se encuentran los divisores y se van contando y sumando hasta completar el
valor de d(N) y σ(N). Si esta media es
entera, el número N será armónico.
Incluimos
un listado en Basic que lo logra:
Sub
armonico
Input
n
a=0
‘Inicia el contador de divisores
b=0
‘Inicia el sumador de divisores
for
j=2 to n/2+1
if
esmultiplo(n,j) then
a=a+1
‘Se ha encontrado un divisor: se
aumenta el contador en 1
b=b+j
‘Se aumenta el sumador con el valor
del divisor
end
if
next
j
a=a+2
‘Se añade 2 para contar también 1 y
N
b=b+n+1
‘Se añaden al sumador 1 y N
m=i*a/b ‘Media
armónica
if
m=int(m) then msgbox(“Es armónico”) else msgbox(“No es armónico”)
end
sub
La
siguiente tabla se ha obtenido con la repetición de este algoritmo:
|
N |
D |
S |
M |
|
6 |
4 |
12 |
2 |
|
28 |
6 |
56 |
3 |
|
140 |
12 |
336 |
5 |
|
270 |
16 |
720 |
6 |
|
496 |
10 |
992 |
5 |
|
672 |
24 |
2016 |
8 |
|
1638 |
24 |
4368 |
9 |
También
se logra la sucesión de números de Ore con el Buscador de naturales:
En la primera condición reproducimos la fórmula obtenida más arriba, y en la segunda publicamos el resultado entero en la segunda columna.
Los
primeros números de Ore son: 1, 6, 28, 140, 270, 496, 672, 1638, 2970, 6200,
8128, 8190,…( https://oeis.org/A001599)
El
listado incluye los números perfectos 6,
28, 496, 8128,…y otros más que no lo son.
Podemos
entender su presencia con los números perfectos conocidos, que siguen la
fórmula 2n–1(2n–1) con el paréntesis primo. Entonces, ese
factor tendrá dos divisores, y por la propiedad multiplicativa, la función TAU
del número perfecto será par. Aplicamos la fórmula que vimos anteriormente
Resulta que SIGMA(N)/N=2 en los números perfectos, con lo que la fórmula queda como d(N)/2, y al ser par el numerador, será entera, y el número será de Ore.
Estos
números no han de ser aritméticos, porque la media aritmética de los divisores no
ha de ser entera. Si lo es, tendremos unos números que pertenecerán a las dos
clases, los aritméticos y los de Ore. Los primeros son
1,
6, 140, 270, 672, 1638, 2970, 6200, 8190, 18600, 18620, 27846, 30240, 32760,
55860, 105664, 117800, 167400,…(
https://oeis.org/A007340)
Podemos considerar la media contrarmónica de los divisores de un número. Ya se estudió aquí el caso particular de cuando sólo intervienen dos números en la media
(ver https://hojaynumeros.blogspot.com/2021/01/media-contraarmonica-entera.html)
En su aplicación a los divisores de un número, esta media se puede
calcular dividiendo la función SIGMA_2(N) entre SIGMA_1(N), es decir, la suma
de los cuadrados de los divisores entre la suma de los mismos.
Este cociente no tiene por qué ser entero. Si lo es, el número N se
llama antiarmónico, porque esta media
también recibe el nombre de “antiarmónica”.
Si se cuenta con la familia de sigmas según el exponente al que
elevamos los divisores, no es difícil encontrar el cociente y comprobar si es
entero. Si no se desea usar estas funciones, y también para traducir la
búsqueda a otro lenguaje de programación, proponemos esta función:
Function esantiaritmetico(n) As Boolean
Dim i, s1, s2, a
s1 = n ‘Suma de
divisores
s2 = n ^ 2 ‘Suma de
cuadrados de divisores
For i = 1 To n / 2
If n / i = n \ i Then s1 = s1 + i: s2 = s2 + i ^ 2
Next i
a = s2 / s1
If a = Int(a) Then esantiaritmetico = True Else esantiaritmetico =
False
End Function
Por cualquiera de estos procedimientos, se encuenran rápidamente los primeros números antiarmónicos:
En PARI el planteo es mucho más simple:
is(n)=sigma(n,2)%sigma(n,1)==0
for(i=1,10^3,if(is(i),print1(i,", ")))
1, 4, 9, 16, 20, 25, 36, 49, 50, 64, 81, 100, 117, 121, 144, 169, 180, 196, 200, 225, 242, 256, 289, 324, 325, 361, 400, 441, 450, 468, 484, 500, 529, 576, 578, 605, 625, 650, 676, 729, 784, 800, 841, 900, 961, 968, 980,
Llama la atención el hecho de que están presentes todos los cuadrados.
Profundizamos algo más con la ayuda de las fórmulas de las sigmas.
En este caso deberemos dividir la sigma de segundo orden entre la de
primero. Nos quedaría:
Simplificando:
Por ejemplo, la media contraarmónica de 200 aparece en la tabla como 119. Lo podemos comprobar con esta fórmula:
M(200)=M(23*52)=(24+1)/(2+1)(53+1)/(5+1)=17/3*126/6
M(200)=17*126/18=119
Es elemental el hecho de que la suma de potencias impares es divisible
entre la suma de las bases, luego la media será entera si los exponentes ei son pares, lo que
demuestra que todos los cuadrados han de figurar en el listado.
Una consecuencia de esto es la de que si un número pertenece a ella y
los multiplicamos por un cuadrado primo con él, por la propiedad
multiplicativa, el resultado pertenecerá a la sucesión (Charles R Greathouse
IV, Aug 02 2013)
Por ejemplo, 20 pertenece a la sucesión y lo podemos multiplicar por 72.
Quedaría:
M(20*72)=M(22*5*72)=(23+1)/(2+1)*(52+1)/(5+1)*(73+1)/(7+1)=9/3*26/6*344/8=559,
luego el producto es antiarmónico.
Esta propiedad garantiza la infinitud de los números antiarmónicos.
Si en estos productos eliminamos los cuadrados, nos quedarán los
llamados antiarmónicos primitivos, que están publicados en https://oeis.org/A228023
1, 20, 50, 117, 200, 242, 325, 500, 578, 605,
650, 800, 968, 1025, 1058, 1280, 1445, 1476, 1682, 1700, 2312, 2340, 2600,
2645, 3200, 3362, 3757, 3872, 4205, 4232,…
Todos los ejemplos encontrados poseen una parte cuadrada mayor que 1,
salvo el caso del mismo 1. Hemos buscado hasta 10^7 términos libres de
cuadrados, sin encontrar ninguno, salvo el 1. Queda como conjetura el hecho de
que no se encontrará ninguno.




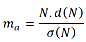




No hay comentarios:
Publicar un comentario