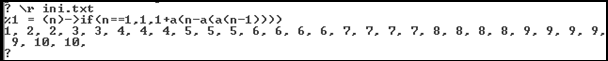Este blog es un complemento natural de mi página http://www.hojamat.es. Por ello, se dedicará a los temas numéricos tratados con Hoja de Cálculo y a la estructura y prestaciones de esta. Su nivel será elemental o medio, y su orientación lúdica e investigadora.
lunes, 21 de diciembre de 2015
Números belgas
Estos números han sido introducidos por Eric Angelini y publicados en el año 2005 en http://oeis.org/A106039. Hay varios tipos, por lo que comenzaremos con los 0-Belgas. Estos números tienen la propiedad de que si a partir del número 0 vamos sumando reiteradamente las cifras (por orden) del número dado, se forma una sucesión que contiene a ese número. Por ejemplo, el 18 es 0-belga, porque a partir del 0 vamos a ir sumando sucesivamente 1, 8, 1, 8,…hasta llegar o sobrepasar el 18: 0, 1, 9, 10, 18, resultando que el mismo 18 es término de la sucesión. Sin embargo, el 19 no lo es, porque se forma la sucesión 0, 1, 10, 11, 20, 21, 30,…al ir sumando sucesivamente 1, 9, 1, 9,… y el mismo 19 es sobrepasado sin pertenecer a la sucesión. Se llaman 0-belgas porque la sucesión la comenzamos en 0, y los primeros son estos:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 17, 18, 20, 21, 22, 24, 26, 27, 30, 31, 33, 35, 36, 39, … http://oeis.org/A106039
Si un número posee 3, 4 o más cifras, estas se irán también sumando de forma sucesiva y ordenada.
Llamaremos n-belgas a aquellos números que pertenecen a la sucesión formada al sumar cifras, pero comenzando en el número n, siendo n menor que el número dado. Así, estos son los 1-belgas:
1, 10, 11, 13, 16, 17, 21, 23, 41, 43, 56, 58, 74, 81, 91, 97, 100, 101, 106, 110,… http://oeis.org/A106439
Por ejemplo, el 23, comenzando en 1, genera con las cifras 2 y 3 la sucesión 1, 3, 6, 8, 11, 13, 16, 18, 21, 23,…a la que él mismo pertenece.
Se han publicado también los 2-belgas (A106518), los 3-belgas (A106596) y otros.
Función ESBELGA
Dado un número cualquiera, es posible saber si es 0-belga, 1-belga o de rango superior. Podemos idear una función con dos parámetros, uno, el número dado, y otro, el tipo. Como el objetivo de esta entrada es experimentar y descubrir curiosidades, daremos dos versiones de esta función, una un poco larga, antes de reflexionar sobre la cuestión, y otra simplificada.
En primer lugar pensamos en lo obvio:
* Deberemos extraer las cifras del número
* Después las iremos sumando ordenadamente a partir del número tipo
* Proseguimos hasta llegar o sobrepasar el presunto número belga
* Si un término de la sucesión coincide con el número dado, es que sí es belga.
Algo así, en el Basic VBA:
Function esbelga(n, t) ‘Los parámetros son el número y el tipo
Dim c(10) ‘Se reserva un vector para almacenar hasta diez cifras (se puede ampliar)
Dim i, nu, a, b, m, p
Dim es As Boolean
‘En primer lugar se extraen las cifras y se almacenan
i = 0: m = n
While m > 0
p = m - 10 * Int(m / 10)
i = i + 1
c(i) = p ‘memorias que guardan las cifras
m = Int(m / 10)
Wend
nu = i
‘Iniciamos la prueba para ver si es belga
es = False
i = 1: a = t ‘La variable a se inicia en el tipo
While a < n ‘Creamos una sucesión hasta n
m = i Mod nu: If m = 0 Then m = nu
a = a + c(nu - m + 1) ‘Se van sumando las cifras a la variable a
i = i + 1
If a = n Then es = True ‘Si la sucesión coincide con n, es belga
Wend
esbelga = es
End Function
Esta función resulta lenta para valores grandes de n, ya que contiene demasiados ciclos de suma de cifras. Sería más práctico eliminar todo esos ciclos dividiendo de forma entera n-t (siendo t el tipo de belga) entre la suma de sus cifras. Para números pequeños no se advierte diferencia en la rapidez del algoritmo, pero siempre debemos intentar simplificar. También se puede usar la función MOD para acelerar la extracción de cifras. Quedaría así:
Function esbelga(n, t) As Boolean
Dim c(10)
Dim i, nu, a, m, p, s
Dim es As Boolean
i = 0: m = n: s = 0
While m > 0
p = m Mod 10
i = i + 1
c(i) = p: s = s + p ‘Extracción de cifras en orden inverso
m = Int(m / 10)
Wend
nu = i
a = (n - t) Mod s ‘Se eliminan los ciclos de suma de cifras
i = 1
If a = 0 Then ‘Si el número es múltiplo de la suma de cifras, es belga
es = True
Else
es = False
For i = 1 To un ‘Se eliminan cifras de la suma para ir probando
If Abs(a - s) < 1 Then es = True ‘Debería escribirse a=s, pero así eliminamos problemas de coma flotante
If Not es Then s = s - c(i)
Next i
End If
esbelga = es
End Function
Por si deseas experimentar, esta es la versión de la función para PARI:
esbelga(n,p)={s=0;k=0;x=n;while(x>0,s+=x%10;x=(x-x%10)/10;k++);
r=(n-p)%s;t=s;x=n;e=0;for(j=0,k,if(r==t,e=1);t-=x%10;x=(x-x%10)/10;);
return(e);}
En la imagen se han generado con esta función los belgas de tipo 0, 1 y 2:
Algunas propiedades
Esta idea de eliminar previamente todos los ciclos de suma de cifras permite afirmar algo más:
Si un número es divisible entre la suma de sus cifras, será 0-belga.
En efecto, al sumar n ciclos de suma de cifras llegamos a n sin tener que recorrer la sucesión. Estos números son los llamados Números Harshad o de Niven:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 18, 20, 21, 24, 27, 30, 36, 40, 42, 45, 48, 50, 54, 60, 63, 70,… http://oeis.org/A005349
Aplícale a cualquiera de ellos la función ESBELGA con parámetro 0 y deberá devolverte siempre VERDADERO.
El número de k-belgas, para cualquier valor de k, es infinito.
Bastará sumar a k todos los múltiplos de la suma de cifras de cualquier otro número.
Todo número es k-belga para algún valor de k.
Porque k puede ser el resto de dividir n entre la suma de sus cifras.
Números autobelgas
Puede darse la casualidad de que un número que comienza por la cifra k, sea también k_belga. Por ejemplo, el 25 tiene como primera cifra el 2, y 2-belga.
Esto no pasa de ser un divertimento, como todo el tema, pero nos permite crear una función:
Function autobelga(n)
Dim c, l
l = Len(Str$(n)) – 1 ‘Extrae el número de cifras
If l = 1 Then c = n Else c = Int(n / 10 ^ (l - 1)) ’Extrae la oprimera cifra
If esbelga(n, c) Then autobelga = True Else autobelga = False ‘Comprueba si es belga
End Function
Con ella es fácil crear listados de autobelgas. En la imagen se han listado los comprendidos entre 10 y 30:
Están publicados en http://oeis.org/A107062
Estos números se llaman autobelgas de primer tipo. Hay otros de segundo, en los que además de coincidir la primera cifra con el tipo, también lo hace la segunda con la primera cifra del segundo término. No merece el tema tanta complicación. Te dejamos que busques información y experimentes.
miércoles, 9 de diciembre de 2015
Volvemos a los números "arolmar" (1) Historia y generación
Esta entrada y otras siguientes que aparecerán sobre el mismo tema suponen un regreso a una sucesión que ideamos en 2011, cuya originalidad atrajo a nuestro colaborador Rafael Parra, que fue quien le dio el nombre de “números arolmar”. Tanto él como el autor publicaron sobre el tema en OEIS (The On-line Encyclopedia of integer sequences). Ahora, transcurridos cuatro años, hemos querido desarrollar con tranquilidad la generación de esos números, así como sus propiedades, curiosidades y otras sucesiones afines.
No busque el lector profundidad en esta serie. Se trata tan sólo de exprimir a nivel descriptivo las posibilidades que nos ofrece esta sucesión, sin plantearnos otros objetivos.
Es posible que la publicación no se efectúe de forma consecutiva, a fin de no bloquear el blog si surgen cuestiones de actualidad. Pueden aparecer siete o más entradas distintas.
Historia
Con fecha 23/2/2011 se publicó en este blog una pequeña entrada titulada “Primos por todas partes” (http://hojaynumeros.blogspot.com.es/2011/02/primos-por-todas-partes.html) En ella se presentaba la sucesión
21, 33, 57, 69, 85, 93, 105, 129, 133, 145, 177, 195,…
Son números compuestos que tienen todos sus factores primos distintos (son números libres de cuadrados) y el promedio de esos factores es un número primo.
Por ejemplo 145=5*29, y el promedio de ambos es (5+29)/2= 17, que es primo.
195=3*5*13, y el promedio es (3+5+13)/3 = 21/3 = 7, también primo.
Posteriormente se publicó esta sucesión en OEIS (https://oeis.org/A187073), y Rafael Parra Machío les dio el nombre de números arolmar, dedicándoles un estudio publicado en http://hojamat.es/parra/arolmar.pdf
Dado el interés del tema, ampliaremos la búsqueda de esos números y estudiaremos algunos detalles más sobre esta sucesión y otras afines. Nos moveremos en un nivel de profundidad de tipo medio, que es el que domina el autor, sin pasar a cuestiones de criptosistemas, muy bien explicados en el documento de Rafael Parra. Nuestro objetivo será el de ampliar las formas de generarlos, estudiar alguna subsucesión y buscar números con propiedades similares.
En esta primera entrada reflexionaremos sobre su generación con varias herramientas.
Generación de la sucesión
Con el Buscador de Naturales
En el documento http://www.hojamat.es/publicaciones/Hojanum3.pdf publicamos la forma de encontrar estos números con nuestro Buscador de números naturales (http://www.hojamat.es/sindecimales/divisibilidad/herramientas/herrdiv.htm#global)
Basta leer las cuatro líneas de condiciones necesarias para entender la gran potencia de este buscador:
Si lo descargas y escribes las cuatro condiciones en la zona dedicada a ellas obtendrás los primeros términos de la sucesión:
En la primera columna figuran los términos y en la segunda el número primo promedio de los factores primos de los mismos.
La primera condición exige que el promedio de factores primos sea también primo. La segunda lo presenta. La tercera exige que esté libre de cuadrados, y la cuarta que no sea primo.
Con el Basic de las hojas
Al ser el Buscador una herramienta no contrastada, puede ser bueno comprobar los resultados con otros instrumentos. En este blog solemos usar el Basic de las hojas de cálculo. Si tenemos definidas las funciones pertinentes, la búsqueda se reduce a un simple bucle FOR-NEXT
Necesitamos las funciones
PARTECUAD
Te devuelve la parte cuadrada de un número natural. Si esa parte vale 1, es que el número es libre de cuadrados. La tienes en
http://hojaynumeros.blogspot.com.es/2011/05/parte-cuadrada-y-parte-libre-solucion.html
Se puede encontrar escribiendo PARTECUAD en Google.
ESPRIMO
La hemos usado mucho en este blog. La puedes encontrar en nuestra hoja sobre conjeturas
http://www.hojamat.es/sindecimales/divisibilidad/herramientas/herrdiv.htm#global
SOPF y F_OMEGA
(o SOPFR Y BIGOMEGA, que en libres de cuadrados son equivalentes)
La primera suma los factores y la segunda los cuenta. Su cociente dará el promedio.
En la entrada http://hojaynumeros.blogspot.com.es/2013/11/de-donde-vengo-3-sumamos-y-contamos.html damos algunas ideas sobre ellas.
Bucle
Con esas funciones y alguna otra podemos ya construir nuestro bucle de búsqueda:
For i = 2 to 1000
If Not esprimo(i) And partecuad(i) = 1 Then
b = sopf(i) / f_omega(i)
If esentero(b) And esprimo(b) Then msgbox(i)
End If
Next i
Implementando un programa similar en una hoja en la que los resultados aparecen bien ordenados, obtenemos los mismos resultados que con el Buscador:
En la primera columna figuran los números arolmar y en la segunda el promedio (primo) de sus factores primos.
Existen infinitos números arolmar, según veremos en la próxima entrada, siempre que se admita la conjetura de Goldbach. En el gráfico de los primeros de ellos (hasta una cota de 2000) se percibe una clara tendencia lineal, que en este intervalo presenta una pendiente aproximada de 17 con un ajuste de nivel 0,9971. Podemos esperar un número arolmar en cada incremento de 17.
Más incidencias presenta la distribución de los números primos que son promedio de sus factores:
En el gráfico distinguimos fácilmente varias líneas de tendencia ¿Adivinas la causa? Pues sí, depende del número de factores que intervengan en el promedio. La línea superior corresponden a los números arolmar que son semiprimos, la siguiente a los que tienen tres factores, y las de más abajo, que llegan a hacerse indistinguibles, a los números que poseen más factores aún. Como también veremos en utra entrada, este gráfico recorre todos los primeros números primos.
Código PARI
En la sucesión A187073 figura un código generador debido a Charles R Greathouse IV
isA187073(n)=my(f=factor(n)); #f[, 1]>1&vecmax(f[, 2])==1&denominator(f=sum(i=1, #f[, 1], f[i, 1])/#f[, 1])==1&isprime(f)
Como puede resultar incomprensible, por compacto, lo sustituiremos por otro más sencillo (y largo), pero que nos permitirá ir explicando las funciones que necesitamos:
freesqrcomp(n)=issquarefree(n)&&!isprime(n)
sopf(n)= { local(f, s=0); f=factor(n); for(i=1, matsize(f)[1], s+=f[i, 1]); return(s) }
averg(n)={local(s); s=sopf(n)/omega(n); return(s)}
{ for (n=4, 10^3, if(freesqrcomp(n), m=averg(n);if(m==truncate(m),if(isprime(m), print1(n, ", ")))))}
En él se van implementando las condiciones exigidas a los números buscados.
Carácter de número compuesto libre de cuadrados:
Basta definir esta función.
freesqrcomp(n)=issquarefree(n)&&!isprime(n)
En ella exigimos que sea libre de cuadrados (issquarefree) y que no sea primo (!isprime(n)). El signo “!” representa la conectiva NO y && la conjunción Y. Si escribes a continuación “{print(freesqrcomp(30))}” la respuesta será 1, que significa VERDADERO, pues 30=2*3*5 es compuesto y libre de cuadrados. Ya tenemos el primer paso: identificar los números de este tipo.
Función SOPF
sopf(n)= { local(f, s=0); f=factor(n); for(i=1, matsize(f)[1], s+=f[i, 1]); return(s) }
Esta parte es más difícil de entender. Esta función suma los factores primos de un número sin contar las repeticiones. En PARI la matriz (o vector) factor(n) contiene los factores primos en la primera columna y sus exponentes en la segunda. La variable s suma sólo los factores primos, pero no sus exponentes. Por eso se escribe s+=f[i, 1])
Promedio de los factores primos
averg(n)={local(s); s=sopf(n)/omega(n); return(s)}
Se basa en la función anterior SOPF y en OMEGA, que cuenta los factores primos sin repetición. Por tanto, su cociente es el promedio de los factores primos.
Bucle de búsqueda
{ for (n=4, 10^3, if(freesqrcomp(n), m=averg(n);if(m==truncate(m),if(isprime(m), print1(n, ", ")))))}
Lo que queda es ya recorrer los números (en el ejemplo desde 4 hasta 1000) e imprimir aquellos cuyo promedio de factores primos es entero (m==truncate(m)) y primo (isprime(m))
Aquí tienes la pantalla con el resultado:
Hemos querido detenernos en esta generación en PARI porque usaremos más adelante códigos similares.
Por último, incluimos la función ESAROLMAR, que nos devuelve VERDADERO si su argumento es un número arolmar. Con ella se pueden emprender otras búsquedas y encontrar curiosidades.
Función ESAROLMAR
Con el Basic de las hojas de cálculo podría tener esta estructura:
Public Function esarolmar(n)
Dim es As Boolean
Dim b
es = False
If Not esprimo(n) And partecuad(n) = 1 Then
b = sopf(n) / f_omega(n)
If esentero(b) And esprimo(b) Then es = True
End If
esarolmar = es
End Function
La segunda línea exige que el número no sea primo (Not esprimo(n))y que sí sea libre de cuadrados, o bien que su parte cuadrada sea igual a 1 (partecuad(n) = 1), que son las dos condiciones iniciales de la definición de número arolmar.
En la siguiente se calcula la media de los factores primos, dividiendo su suma (sopf(n)) entre su número (f_omega(n)) y, por último, se exige que el resultado sea entero y primo.
La versión con PARI necesita la definición progresiva de varias funciones:
freesqrcomp(n)=issquarefree(n)&&!isprime(n)
sopf(n)= { local(f, s=0); f=factor(n); for(i=1, matsize(f)[1], s+=f[i, 1]); return(s) }
averg(n)={local(s); s=sopf(n)/omega(n); return(s)}
esarolmar(n)={local(a=averg(n),s);s=freesqrcomp(n)&&a==truncate(a)&&isprime(a); return(s)}
{for(i=2,1000,if(esarolmar(i),print(i)))}
La última línea presenta todos los números arolmar hasta el 1000.
En la siguiente entrada sobre este tema estudiaremos el carácter impar de estos números y cómo aparecen sus diferencias (arolmar gemelos, cousin, sexy,...)
Recuerda que esta serie no se publicará de forma consecutiva. Intercalaremos otros temas y para el verano resumiremos todo en una publicación,
lunes, 30 de noviembre de 2015
Primos de Fibonacci
Hoy estudiaremos otra conjetura bastante popular:
Existen infinitos números de Fibonacci que son primos.
Así que si construimos la sucesión de Fibonacci y elegimos los términos que sean primos, encontraremos uno de ellos que sea mayor que cualquier otro entero que imaginemos. Aprovecharemos esta conjetura para repasar conceptos, construir algoritmos y explicar algunas propiedades de los números de Fibonacci.
Los primeros primos de Fibonacci son estos:
2, 3, 5, 13, 89, 233, 1597, 28657, 514229, 433494437, 2971215073, 99194853094755497,…
(http://oeis.org/A005478)
Según la conjetura, esta sucesión debería tener infinitos términos. No es intuitivo, porque en cada aumento de índice resulta más improbable que el término correspondiente sea primo, pero así son las conjeturas, que se encuentran a veces en el término de separación entre lo imposible e improbable.
Comprobación de la conjetura
En la hoja Conjeturas
(http://www.hojamat.es/sindecimales/divisibilidad/herramientas/herrdiv.htm#conjeturas)
dispones de las funciones necesarias para comprobar la conjetura, se entiende que en unos pocos ejemplos. La primera, ESPRIMO, ya ha sido presentada muchas veces en este blog (escribe ESPRIMO HOJA en un navegador de Internet), pero necesitamos otra, ESFIBO, que nos indica si un número pertenece o no a la sucesión de Fibonacci. Esta función se basa en un popular criterio para saber si un número es de Fibonacci o no: Un número N pertenece a la sucesión de Fibonacci si y sólo si 5N2+4 o 5N2-4 es un cuadrado perfecto.
(Ver http://gaussianos.com/algunas-curiosidades-sobre-los-numeros-de-fibonacci/)
Según eso, ésta puede ser la función que devuelva VERDADERO si un número es del tipo Fibonacci y FALSO en el caso opuesto:
Public Function esfibo(n) As Boolean 'devuelve verdadero si N es de Fibonacci
Dim f As Boolean
Dim a
f = False
a = 5 * n * n + 4
If escuad(a) Then f = True
a = 5 * n * n - 4
If escuad(a) Then f = True
esfibo = f
End Function
Disponiendo de esta función y de la ESPRIMO, podemos construir otra, a la que llamaremos FIBOPRIMPROX, que, dado un entero positivo, devuelva el menor primo Fibonacci que es mayor que él, es decir, el “próximo primo Fibonacci”. Su código sería:
Function fiboprimprox(a) As Long
Dim p, prim As Long
Dim sale As Boolean
'Encuentra el menor primo de Fibonacci mayor que el dado
p = a + 1: sale = False: prim = 0
While Not sale
If esprimo(p) And esfibo(p) Then prim = p: sale = True
p = p + 1
Wend
fiboprimprox = prim
End Function
Se entiende fácilmente. El problema, como ocurre frecuentemente en este blog, es que la hoja de cálculo tiene una capacidad limitada de cálculo con enteros. Por ello, con la hoja CONJETURAS sólo hemos podido llegar al próximo a 100000.
Observa que los números de la segunda columna pertenecen a la sucesión de primos Fibonacci. El siguiente, 433494437, sería difícil de obtener con este procedimiento.
Si la conjetura es cierta, la función FIBOPRIMPROX(N) debe devolver un resultado por muy grande que sea N.
Como procedemos a menudo en este blog, traducimos el proceso a PARI para ver si podemos reproducir más elementos de la sucesión. Hemos optado por este código:
{for(i=1,10^4,f=fibonacci(i);if(isprime(f),print(f)))}
El resultado ha sido impresionante, porque en pocos segundos nos ha devuelto los primos contenidos en los 10000 primeros términos de la sucesión de Fibonacci:
Si en el código PARI hubiéramos pedido el valor del índice en lugar del término de Fibonacci nos hubiera resultado la sucesión:
3, 4, 5, 7, 11, 13, 17, 23, 29, 43, 47, 83, 131, 137, 359, 431, 433, 449, 509, 569, 571, 2971, 4723, 5387, 9311, 9677,…
Como se ve, salvo el caso del 4, todos los índices de números de Fibonacci primos son también primos. Esto se deriva de que si p divide a q, Fp también divide a Fq para p,q>=3. Así que si el número de orden no es primo, tampoco lo será el número Fibonacci correspondiente. La propiedad recíproca no es cierta. Por ejemplo, el término de índice 19, primo, es 4181=37*113, compuesto.
Divisibilidad en los números Fibonacci
La cuestión anterior da pie a que revisemos algunas propiedades interesantes que presentan los factores primos de los términos de esta sucesión.
El máximo común divisor
Los términos de la sucesión de Fibonacci cumplen la siguiente curiosa propiedad:
Por ejemplo, si elegimos los términos 24 y 36 de la sucesión,
F(24) = 46368 =25*32*7*23 y F(36) = 14930352 = 24*33*17*19*107, tendremos
MCD(46368, 14930352) = 144, MCD(24, 36) = 12 y F(12)=144
Por tanto, si el índice de un número de Fibonacci es primo, éste será coprimo con el anterior y el siguiente. Obviamente, esto lo cumplirán los primos Fibonacci, pero también el contraejemplo que vimos más arriba, F(19) = 4181. En la tabla verás la falta de elementos comunes con el anterior y el siguiente elemento Fibonacci.
Teorema de Carmichael
Relacionado con este tema de divisores de los números Fibonacci disponemos de este interesante teorema:
Todo término de la sucesión de Fibonacci distinto de 1, 8 y 144, posee un factor primo que no divide al anterior término.
Lo puedes comprobar en esta tabla de divisores de los términos 10 a 20:
Todo término posee un factor primo que no divide al anterior (recuerda que el segundo número de cada corchete es el exponente del factor primo).
Puede ocurrir que un factor dado no divida a ningún otro término anterior. Por ejemplo, el factor 41 de F(20) no divide a ningún término anterior. En este caso le llamaremos factor característico o primitivo. Los tienes en https://oeis.org/A001578.
jueves, 19 de noviembre de 2015
Sucesión de Golomb
Ya estudiamos en 2010 conjuntos relacionados con este matemático
http://hojaynumeros.blogspot.com.es/2010/03/jugamos-con-sidon-y-golomb.html
Hoy lo hacemos con una de sus sucesiones. Se trata de esta:
1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12,…
http://oeis.org/A001462
También se la conoce como sucesión de Silverman. Como ves, es no-decreciente.
Tiene una definición muy curiosa, y es que a(n) representa el número de veces que aparece n en la sucesión, si además definimos a(1)=1 e implícitamente aceptamos que cada valor de n ocupa el mínimo número de orden posible.
Lo verás mejor si acompañamos cada valor con su índice:
La imagen de 1 es 1 por definición. La de 2 es 2 porque en la sucesión figura ese valor dos veces. También el 3 aparece repetido, por lo que a(3)=2. A(4)=3 debido a que aparecen tres cuatros, y así con todos.
Este es un ejemplo muy elegante de autorreferencia, pues se define un objeto como si ya estuviera construido, pero sólo lo podemos formar si seguimos la definición.
Si aceptamos la condición de que cada valor ocupe el primer número de orden que esté libre, y que cada nueva imagen es la menor que cumple a(n)>=a(n-1), esta sucesión es única. En efecto, nos ponemos a razonar:
A(1)=1 por definición, luego sólo existirá un 1 en la sucesión, por lo que la imagen de 2 no podrá ser 1. Según las condiciones, ha de ser 2, luego en la sucesión deberá haber un par de 2. Como hemos quedado en que se ocupan los menores números de orden, deberá quedar:
Esto significa que a(3)=2, luego también repetiremos el 3 dos veces:
Obligamos así a que el 4 y el 5 figuren tres veces:
Ya podrás seguir tú el razonamiento y completar la sucesión, que con las condiciones impuestas será única.
¿Lo podría conseguir una hoja de cálculo? La respuesta es afirmativa, y el algoritmo no es muy complejo. Necesitamos dos punteros, indi1, que recorrerá los valores de n, e indi2 que llevará la cuenta de los lugares que van quedando libres en la sucesión. Con indi1 se leen los valores, y con indi2 se escriben. Para evitar celdas vacías en los primeros valores, se rellenan el 1 y el 2. Quedará así con el Basic de las hojas:
Sub golomb()
Dim indi1, indi2, i, j, v
indi1 = 2 ‘El primer valor que se lee es el 2, en la celda (2,2)
indi2 = 2 ‘El primero que se escribe también es el 2
Cells(1, 2).Value = 1 ‘Rellenamos los dos primeros valores en las celdas (1,2) y (2,2)
Cells(2, 2).Value = 2
For i = 1 To 12 ‘Tomamos 12 valores, pero podían ser muchos más
v = Cells(indi1, 2).Value ‘Leemos el valor indicado por indi1 (que también es fila en la hoja)
For j = 1 To v ‘Escribimos tantos valores nuevos como indique v
Cells(indi2, 2).Value = indi1 ‘Todos los valores serán iguales a indi1
indi2 = indi2 + 1 ‘Avanza la escritura
Next j
indi1 = indi1 + 1 ‘Avanza la lectura
Next i
End Sub
Con esta subrutina se generará la sucesión de Golomb en la columna 2 de una hoja de cálculo:
Para mayor claridad hemos copiado los resultados en varias columnas, manualmente. Observarás que se reproducen fielmente los valores deseados.
La forma de generación de esta sucesión garantiza que a(n)<=n, ya que los valores de los números naturales aparecen “con retraso”, y cuando aparece el valor, el índice ha crecido más que él. El retraso se puede medir con la diferencia n-a(n):
Vemos que los retrasos a partir de 3 son todos positivos y crecientes.
Una propiedad elemental, pero que hay que pensar en ella un poco, es que las sumas parciales de esta sucesión coinciden con el índice de la última aparición en la sucesión del número de sumandos. Más claro: si sumo tres términos, 1+2+2=5, obtengo que la última aparición del 3 ocurrirá en el término 5. Esto es por la propia definición: el 1 aparece una vez, el 2 dos y el 3 otras dos, luego el último 3 aparecerá en el lugar 5.
La sucesión de sumas parciales es
1, 3, 5, 8, 11, 15, 19, 23, 28, 33, 38, 44, 50, 56, 62, 69, 76, 83, 90, 98, 106, 114, 122, 131, 140, 149, 158, 167, 177, 187,… (http://oeis.org/A001463) y coincide con el lugar de la última aparición de su número de orden. Así, si el quinto término es 11, ahí ocurrirá la última aparición del 5.
Según esto, si llamamos F(n) a los términos de la sucesión de Golomb y G(n) a sus sumas parciales, se cumplirá (estúdialo bien) que
Fórmula recurrente
Colin Mallows ha ideado una recurrencia muy atractiva para evaluar F(n):
F(1) = 1; F(n+1) = 1 + F(n+1-F(F(n)))
En hoja de cálculo las recurrencias son posibles, pero si se agota la pila de datos se puede bloquear el cálculo. Lo hemos intentado y funciona bien para los primeros términos, pero no va mucho más allá. En Basic sería
Public Function a(n)
If n = 1 Then
a = 1
Else
a = 1 + a(n - a(a(n - 1)))
End If
End Function
Con ella hemos formado esta tabla
En PARI también funciona la recurrencia, pero no merece la pena porque se va ralentizando para números grandes:
a(n)=if(n==1,1,1+a(n-a(a(n-1))))
{for(i=1,30,print1(a(i),", "))}
Aproximación asintótica
Por lo que hemos leído, no ha sido muy fácil llegar a esta expresión:
La comprobamos gráficamente
Se ve que son prácticamente indistinguibles.
http://hojaynumeros.blogspot.com.es/2010/03/jugamos-con-sidon-y-golomb.html
Hoy lo hacemos con una de sus sucesiones. Se trata de esta:
1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12,…
http://oeis.org/A001462
También se la conoce como sucesión de Silverman. Como ves, es no-decreciente.
Tiene una definición muy curiosa, y es que a(n) representa el número de veces que aparece n en la sucesión, si además definimos a(1)=1 e implícitamente aceptamos que cada valor de n ocupa el mínimo número de orden posible.
Lo verás mejor si acompañamos cada valor con su índice:
La imagen de 1 es 1 por definición. La de 2 es 2 porque en la sucesión figura ese valor dos veces. También el 3 aparece repetido, por lo que a(3)=2. A(4)=3 debido a que aparecen tres cuatros, y así con todos.
Este es un ejemplo muy elegante de autorreferencia, pues se define un objeto como si ya estuviera construido, pero sólo lo podemos formar si seguimos la definición.
Si aceptamos la condición de que cada valor ocupe el primer número de orden que esté libre, y que cada nueva imagen es la menor que cumple a(n)>=a(n-1), esta sucesión es única. En efecto, nos ponemos a razonar:
A(1)=1 por definición, luego sólo existirá un 1 en la sucesión, por lo que la imagen de 2 no podrá ser 1. Según las condiciones, ha de ser 2, luego en la sucesión deberá haber un par de 2. Como hemos quedado en que se ocupan los menores números de orden, deberá quedar:
Esto significa que a(3)=2, luego también repetiremos el 3 dos veces:
Obligamos así a que el 4 y el 5 figuren tres veces:
Ya podrás seguir tú el razonamiento y completar la sucesión, que con las condiciones impuestas será única.
¿Lo podría conseguir una hoja de cálculo? La respuesta es afirmativa, y el algoritmo no es muy complejo. Necesitamos dos punteros, indi1, que recorrerá los valores de n, e indi2 que llevará la cuenta de los lugares que van quedando libres en la sucesión. Con indi1 se leen los valores, y con indi2 se escriben. Para evitar celdas vacías en los primeros valores, se rellenan el 1 y el 2. Quedará así con el Basic de las hojas:
Sub golomb()
Dim indi1, indi2, i, j, v
indi1 = 2 ‘El primer valor que se lee es el 2, en la celda (2,2)
indi2 = 2 ‘El primero que se escribe también es el 2
Cells(1, 2).Value = 1 ‘Rellenamos los dos primeros valores en las celdas (1,2) y (2,2)
Cells(2, 2).Value = 2
For i = 1 To 12 ‘Tomamos 12 valores, pero podían ser muchos más
v = Cells(indi1, 2).Value ‘Leemos el valor indicado por indi1 (que también es fila en la hoja)
For j = 1 To v ‘Escribimos tantos valores nuevos como indique v
Cells(indi2, 2).Value = indi1 ‘Todos los valores serán iguales a indi1
indi2 = indi2 + 1 ‘Avanza la escritura
Next j
indi1 = indi1 + 1 ‘Avanza la lectura
Next i
End Sub
Con esta subrutina se generará la sucesión de Golomb en la columna 2 de una hoja de cálculo:
Para mayor claridad hemos copiado los resultados en varias columnas, manualmente. Observarás que se reproducen fielmente los valores deseados.
La forma de generación de esta sucesión garantiza que a(n)<=n, ya que los valores de los números naturales aparecen “con retraso”, y cuando aparece el valor, el índice ha crecido más que él. El retraso se puede medir con la diferencia n-a(n):
Vemos que los retrasos a partir de 3 son todos positivos y crecientes.
Una propiedad elemental, pero que hay que pensar en ella un poco, es que las sumas parciales de esta sucesión coinciden con el índice de la última aparición en la sucesión del número de sumandos. Más claro: si sumo tres términos, 1+2+2=5, obtengo que la última aparición del 3 ocurrirá en el término 5. Esto es por la propia definición: el 1 aparece una vez, el 2 dos y el 3 otras dos, luego el último 3 aparecerá en el lugar 5.
La sucesión de sumas parciales es
1, 3, 5, 8, 11, 15, 19, 23, 28, 33, 38, 44, 50, 56, 62, 69, 76, 83, 90, 98, 106, 114, 122, 131, 140, 149, 158, 167, 177, 187,… (http://oeis.org/A001463) y coincide con el lugar de la última aparición de su número de orden. Así, si el quinto término es 11, ahí ocurrirá la última aparición del 5.
Según esto, si llamamos F(n) a los términos de la sucesión de Golomb y G(n) a sus sumas parciales, se cumplirá (estúdialo bien) que
F(G(n)) = n
Fórmula recurrente
Colin Mallows ha ideado una recurrencia muy atractiva para evaluar F(n):
F(1) = 1; F(n+1) = 1 + F(n+1-F(F(n)))
En hoja de cálculo las recurrencias son posibles, pero si se agota la pila de datos se puede bloquear el cálculo. Lo hemos intentado y funciona bien para los primeros términos, pero no va mucho más allá. En Basic sería
Public Function a(n)
If n = 1 Then
a = 1
Else
a = 1 + a(n - a(a(n - 1)))
End If
End Function
Con ella hemos formado esta tabla
En PARI también funciona la recurrencia, pero no merece la pena porque se va ralentizando para números grandes:
a(n)=if(n==1,1,1+a(n-a(a(n-1))))
{for(i=1,30,print1(a(i),", "))}
Aproximación asintótica
Por lo que hemos leído, no ha sido muy fácil llegar a esta expresión:
La comprobamos gráficamente
Se ve que son prácticamente indistinguibles.
lunes, 9 de noviembre de 2015
Damos vueltas a los triangulares cuadrados (2). Curiosidades.
En la anterior entrada generamos los números que son a la vez triangulares y cuadrados mediante varios algoritmos y fórmulas directas, tanto para hojas de cálculo como en el lenguaje PARI, e incluso a través de una función recursiva. En esta segunda entrada veremos algunas de sus propiedades y curiosidades sobre ellos.
Otra recurrencia
Según un comentario incluido en http://oeis.org/A001110, podemos tener en cuenta otra recurrencia a partir de n=3:
En efecto, 1225=(36-1)2/1, 41616=(1225-1)2/36, … O con hoja de cálculo:
Intenta averiguar cómo crear esta tabla siguiendo la recurrencia. La podemos expresar también como que la media geométrica entre el anterior y el siguiente a un término coincide con el cuadrado de ese término al que se le ha restado una unidad.
Una propiedad similar es que la media geométrica entre un término y el siguiente es también un número triangular. Lo tienes en esta tabla. Escribe los triangulares cuadrados e intenta después reproducirla:
En http://oeis.org/A029549 tienes estudiadas esas medias geométricas y puedes descubrir que estos números son oblongos y también su conexión con ciertas ternas pitagóricas. A partir de esta sucesión se abren tantos caminos que es mejor parar aquí.
Por otra parte, por ser cuadrados, los términos son suma de dos triangulares consecutivos, luego los triangulares cuadrados son “triangulares suma de dos triangulares consecutivos”
Raíz cuadrada
Ya que tratamos con cuadrados, sería interesante estudiar sus raíces cuadradas, que son estas:
0, 1, 6, 35, 204, 1189, 6930, 40391, 235416, 1372105, 7997214, 46611179, 271669860,…
(http://oeis.org/A001109)
Estos números no nos son desconocidos, pues son soluciones de la incógnita Y en la ecuación de Pell que usamos para encontrar sus cuadrados
Insertamos de nuevo la tabla que obtuvimos:
Más adelante veremos valores relacionados con la variable X.
Recurrencia entre las raíces
Al igual que sus cuadrados, estos números se pueden generar mediante una recurrencia de segundo grado. Para descubrirla operamos como en la entrada anterior
Dn=aDn-1+bDn-2+c usaremos los valores iniciales 0, 1, 6, 35, 204 para plantear:
6=a*1+b*0+c
35=a*6+b*1+c
204=a*35+b*6+c
Resolvemos
29=5a+b
169=29a+5b
169-5*29=169-145=24=4a a=6, b=-1, c=0
Luego Dn=6Dn-1-Dn-2, que es la recursión que figura en A001109
Esta recurrencia la podemos comprobar con nuestra hoja de cálculo dedicada a ellas
http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#recurre2
Escribimos los coeficientes 6 y -1
Y obtenemos la sucesión
Orden como triangulares
Al igual que hemos estudiado las raíces cuadradas de los triangulares cuadrados, también podemos fijar la atención en su orden como triangulares.
Para ello planteamos k(k+1)/2=A(n), siendo A(n) un término de la sucesión de triangulares cuadrados. Es fácil ver que la solución será
Se generará esta otra sucesión:
1, 8, 49, 288, 1681, 9800, 57121, 332928, 1940449, 11309768, 65918161, 384199200,… (http://oeis.org/A001108)
También estos números están relacionados con la ecuación de Pell de la anterior entrada
Basta recordar que llamamos x a 2n+1. Deshaciendo el cambio en la tabla:
(3-1)/2=1, (17-1)/2=8, (99-1)/2=49, (577-1)/2=288,… y así resultarán todos.
Según OEIS, su fórmula recursiva es idéntica a la de los anteriores, pero con término independiente igual a 2:
Dn=6Dn-1-Dn-2+2
Para no cansar a los lectores nos limitamos a comprobarla.
8=6*1-0+2, 49=6*8-1+2, 288=6*49-8+2,…
Diferencias entre términos
Si restamos cada dos términos consecutivos, el resultado coincide con las raíces cuadradas de los términos de orden impar. Es una propiedad muy curiosa, pero no he encontrado ninguna demostración elemental de la misma.
En la tabla, si elevamos las diferencias al cuadrado nos resultan los términos de orden impar. Son los de color rojo enlazados con flechas. Si, además, encontráramos su orden como triangulares, sería un cuadrado (compruébalo), y ellos mismos, además de triangulares serían hexagonales. Bastante curioso, como ves.
Recurrencia directa
Lekraj Beedassy, en http://oeis.org/A001110, propone la siguiente recurrencia no lineal que sólo depende del término anterior:
Esta propiedad permite engendrar de nuevo los números triangulares cuadrados en una hoja de cálculo directamente, sin macros, y con gran rapidez, con una fórmula similar a =1+17*I5+6*RAIZ(I5+8*I5^2), donde puedes sustituir I5 por el término anterior de la sucesión.
miércoles, 28 de octubre de 2015
Damos vueltas a los triangulares cuadrados (1) Generación.
Generación de la sucesión
Dos entradas del blog de John D. Cook (http://www.johndcook.com/blog/2015/08/20/when-is-a-triangle-a-square/ y siguiente) me han animado a volver a tomar el tipo de entrada al que llamé “dar vueltas” a un tema o concepto. Lo haré sobre estos números:
0, 1, 36, 1225, 41616, 1413721, 48024900, 1631432881,… (http://oeis.org/A001110)
Evidentemente, tienen en común el ser triangulares y cuadrados a la vez. Puedes leer un desarrollo sencillo y claro en este documento:
http://www2.caminos.upm.es/Departamentos/matematicas/revistapm/revista_impresa/vol_IV_num_1/jue_mat_num_triang.pdf
Me he dado cuenta de que es un concepto sencillo pero que da lugar a bastantes reflexiones, algoritmos y repasos de teoría.
Nosotros seguiremos en parte este documento para iniciar el tema.
Búsqueda de números triangulares cuadrados
Un número triangular tiene por fórmula n(n+1)/2 y un cuadrado m2. Aquellos números que participen de las dos características tendrán que cumplir la igualdad
De esta igualdad deducimos esta otra mucho más práctica:
O bien
Con cambio de variable se convierte en una ecuación de Pell:
Esta ecuación la tenemos muy estudiada
http://hojamat.es/parra/pell.pdf (documento de Rafael Parra)
http://hojaynumeros.blogspot.com.es/2010/02/ecuacion-de-pell.html
Disponemos además de una hoja de cálculo para ayudar a resolverla:
http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#pell
Usamos esta herramienta para el coeficiente 8 y el segundo miembro 1 y nos dan las primeras soluciones:
(1,0) (3,1) (17,6) (99,35) (577,204) (3363,1189) (19601,6930) (114243, 40391),…
Por recurrencia:
Según la teoría de la ecuación de Pell, las soluciones aparecen con las recurrencias (en este caso) xn=3*xn-1+8*yn-1 yn=3*yn-1+1*xn-1. Por ejemplo, 99=3*17+8*6, 35=3*6+1*17.
Ahora sólo nos queda elevar al cuadrado las soluciones de y (que equivalen a la variable m de la primera igualdad que planteamos) y nos resultarán los triangulares cuadrados:
020, 12=1, 62=36, 352=1225, 2042=41616, 11892=1413721,…
Primer algoritmo
El estudio que acabamos de desarrollar nos da una pista para la generación de términos triangulares cuadrados: Iniciamos dos variables X=1, Y=0, y en cada paso del algoritmo convertimos X en 3X+8Y y la Y en 3Y+X. Terminado el cálculo presentamos el valor de Y2 como siguiente triangular cuadrado. En el Basic de las hojas de cálculo quedaría así:
Sub triangcuad()
Dim x, y, x1, y1, i, t, fila
x = 1: y = 0 ‘Valores de inicio
fila = 3 ‘Fila inicial
Cells(fila, 4).Value = 0 ‘El primer valor es un cero
For i = 1 To 8 ‘Calculamos sólo ocho
x1 = 3 * x + 8 * y ‘Iteración para x
y1 = 3 * y + x ‘Iteración para y
x = x1
y = y1
t = y * y ‘Número triangular cuadrado
fila = fila + 1
Cells(fila, 4).Value = t ‘Se presenta el resultado
Next i
End Sub
Obtendríamos:
El que el último se nos ofrezca en coma flotante nos da idea de las limitaciones de la hoja para cálculos con enteros de muchas cifras. Si acudimos a PARI no nos encontraremos con esas limitaciones. Prueba este código:
{x=1;y=0;print(0);while(x<10^10,x1=3*x+8*y;y1=3*y+x;x=x1;y=y1;t=y^2;print(t))}
En pocos segundos te presenta los triangulares cuadrados menores que 10^10.
Relación de recurrencia con una sola variable
Por la naturaleza de su definición podemos esperar que estos números sigan una relación de recurrencia de segundo orden. Para encontrar su expresión, que será del tipo
An=aAn-1+bAn-2+c usaremos los valores iniciales 0, 1, 36, 1225, 41616 para plantear:
36=a*1+b*0+c
1225=a*36+b*1+c
41616=a*1225+b*36+c
Resolvemos
1189=35a+b
40391=1189a+35b
1224=36a y a=34, b=-1 y c=2
Según los cálculos anteriores, la relación de recurrencia será
An=34An-1-An-2+2
Es la misma que propone John D. Cook en su blog.
En este blog no olvidamos la hoja de cálculo. Intenta una resolución como la de la imagen usando cálculo matricial:
A partir de esta escritura matricial del sistema de ecuaciones, creamos debajo la matriz inversa de los coeficientes con MINVERSA, y a su derecha su producto por los términos independientes con MMULT:
Conseguimos así la misma solución 34, -1, 2
Segundo algoritmo
La relación de recurrencia nos permite un segundo algoritmo para encontrar los triangulares cuadrados. El que describimos a continuación presenta los nueve primeros (después existen problemas de coma flotante)
Sub triancuad1()
Dim m, n, p, k, fila
m = 0: n = 1 ‘Valores iniciales
fila = 3
Cells(1, 3).Value = m ‘presenta los dos primeros términos
Cells(2, 3).Value = n
For k = 1 To 7
p = 34 * n - m + 2 ‘relación de recurrencia
Cells(fila, 3).Value = p: fila = fila + 1 ‘presenta los siguientes términos
m = n: n = p ‘cada término se convierte en el anterior
Next k
End Sub
Los términos rellenarán una columna de hoja de cálculo:
Siguiendo nuestra costumbre, lo traducimos a PARI para conseguir más términos:
{x=0;y=1;print(0);print(1);for (k=1, 20, z=34*y-x+2;print(z);x=y;y=z)}
No resistimos la tentación, al igual que propone J.C. Cook, de intentar una versión recursiva en forma de función. Funciona muy bien en hoja de cálculo:
Public Function ftriangcuad(n)
If n < 2 Then
ftriangcuad = n
Else
ftriangcuad = 34 * ftriangcuad(n - 1) - ftriangcuad(n - 2) + 2
End If
End Function
No necesita explicación. La tabla siguiente se forma con gran rapidez de cálculo:
Fórmula directa
Si lees el capítulo sobre sucesiones recurrentes en nuestra publicación Sucesiones (http://www.hojamat.es/publicaciones/sucesiones.pdf) entenderás que a partir de la fórmula de recurrencia es posible encontrar la expresión directa de cada término (fórmula del término general). Sólo insertamos la captura de pantalla de nuestra hoja de cálculo Recurrencias
(http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#recurre2) en la parte homogénea de la recurrencia:
Con un ligero retoque y la interpretación de los decimales llegamos a la propuesta por John D. Cook:
El uso de la raíz cuadrada de 2 le quita utilidad en nuestro trabajo, por lo que intentaremos prescindir de ella. Para ver la influencia del formato de coma flotante, la implementamos en hoja de cálculo, y el resultado es similar al de los algoritmos anteriores:
Función generatriz
Para quien no lo sepa, diremos que la función generatriz de una sucesión, si se desarrolla como una serie de potencias, poseerá como coeficientes de esas potencias de x los términos de la sucesión.
En el caso de los números triangulares cuadrados la función generatriz es
(ver http://oeis.org/A001110)
Con esta sencilla orden de PARI podemos comprobar su desarrollo.
print(taylor(x*(1+x)/((1-x)*(1-34*x+x^2)),x,20))
Tercer algoritmo
Finalizamos la entrada con la presentación de un algoritmo de los que llamamos “ingenuos”, que no usan la teoría para simplificar los cálculos, pero sí la fuerza bruta de la velocidad de proceso. En este caso obligaremos a los números naturales a ir creciendo hasta alcanzar un cuadrado, y después a la inversa, que los cuadrados avancen hasta alcanzar un triangular. Cuando se llegue a una igualdad se imprime el resultado. A pesar de su simplicidad, no resulta lento. Es éste:
Sub triancuad2()
Dim i, j, m, n, k, fila
m = 3: n = 4: i = 2: j = 3 ‘Se inician las variables
k = 10 ^ 7
fila = 3
Cells(fila, 3).Value = 1: fila = fila + 1
While m < k ‘Busca soluciones menores que k
While m <= n ‘Los triangulares crecen
If m = n Then Cells(fila, 3).Value = m: fila = fila + 1 ‘Hay igualdad
i = i + 1: m = m + i
Wend
While n <= m ‘Los cuadrados crecen
If m = n Then Cells(fila, 3).Value = m: fila = fila + 1 ‘Hay igualdad
j = j + 2: n = n + j
Wend
Wend
End Sub
Dejamos a los lectores el estudio de por qué funciona este algoritmo para descubrir los triangulares cuadrados. Como los anteriores, llega a los mismos resultados, en este caso hasta 10^7.
Suscribirse a:
Entradas (Atom)