(Esta entrada constituye la participación de este blog en el V Carnaval de Matemáticas)
Si reuniéramos en una sola lista los números triangulares, cuadrangulares, pentagonales, etc. ¿llenarían todo el conjunto de los números naturales?
Si reuniéramos en una sola lista los números triangulares, cuadrangulares, pentagonales, etc. ¿llenarían todo el conjunto de los números naturales?
Podemos llamar orden n del número poligonal al número de unidades incluidas en uno de sus lados, y tipo k, al número de lados. Evidentemente, si consideramos los poligonales de orden 1, cualquier número N se puede representar como un polígono de N lados, luego la respuesta es afirmativa.
El problema es más interesante si sólo estudiamos números poligonales de al menos orden 2.
Existen números que son triangulares, como el 10, pentagonales, como el 22, o incluso algunos, como el 28, que son triangulares y hexagonales simultáneamente, como puedes observar en la imagen:
¿Existirán números que sólo puedan considerarse como poligonales de grado uno y no admitan otras representaciones poligonales?
Dado un número cualquiera, como 2011 (el 2010 ya vimos que era poligonal de orden 21), sería interesante averiguar qué representaciones admite como número poligonal. Se puede abordar el problema desde varios puntos de vista. Veamos el más sencillo:
Generación mediante triangulares
Todo número poligonal de orden n y tipo k se puede generar mediante esta fórmula:
Pn,k = n + (k-2)Tn-1
siendo Tn-1 el número triangular de orden n-1.
No es difícil justificar esta fórmula La simple visión de la siguiente imagen te permite comprenderla. Las unidades azules representan a n, y las de los otros tres colores a los números triangulares que terminan de engendrar el pentagonal:
Así que para saber si un número es n-gonal bastará restarle el valor de n y después averiguar si la diferencia contiene a Tn-1 un número entero de veces.
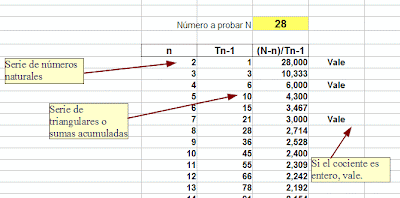
En una hoja de cálculo se pueden organizar tres columnas: La primera con los números naturales n, la segunda con sus sumas acumuladas, que serían los números triangulares T, y en la tercera el cociente (N-n)/T. Si este cociente es entero, hemos descubierto que el número probado es n-gonal.
En la imagen tienes el proceso para descubrir que el número 28 es 28-gonal, hexagonal y triangular. como ya sabíamos.
También podemos comprobar que hay números, como el 2011, que sólo admiten formar un polígono de grado 1 y tipo 2011. Sin embargo, el 2016 admite seis representaciones, con tipos 2016, 673, 136, 24, 6 y 3.
Generación mediante fórmula
De la generación de números poligonales a partir de triangulares se puede deducir la popular fórmula
Pn,k=n(n(k-2)-(k-4))/2
Si la consideramos como ecuación de segundo grado en n, se puede exigir que su discriminante sea cuadrado perfecto, es decir:
D=(k-4)2+8Pn,k(k-2)=M2
Esto nos da otro procedimiento: Recorremos valores de k y observamos cuáles producen cuadrados perfectos y después si el valor de n es entero. En la imagen puedes observar cómo se organiza la búsqueda en hoja de cálculo