Regresos 4: Doblado pitagórico

Ampliamos en esta entrada el contenido de otra similar publicada en este blog en el año 2010:

https://hojaynumeros.blogspot.com/2010/10/1-7-17-23-31-41-47-49-71-73-79-89-97.html

Si tomamos un segmento de longitud 31 cm. y lo doblamos por cierto punto en forma de ángulo recto, podemos completar un triángulo rectángulo cuya hipotenusa tiene medida entera. No es difícil averiguar por dónde se puede doblar: basta hacerlo con un segmento de medida 7, con lo que el otro trozo mediría 24 y la hipotenusa 25, pues 7²+24²=25²

Existen otros números con la misma propiedad: 7, descompuesto en 3 y 4, 23, doblado por 8 y 15, y otros muchos.

Además de 7, 23 o 31, ¿qué otros números tienen la propiedad de engendrar un triángulo rectángulo de medidas enteras con un simple “doblado”?

Podríamos extender el tipo de doblado a conseguir una hipotenusa y un cateto, o bien, con dos dobleces, conseguir los tres lados, que es lo que se efectuó en la Antigüedad para conseguir un ángulo recto con un doblado 3+4+5=12.

Comenzamos:

Doblado en dos catetos

Para poder estudiar simultáneamente varios casos, asignaremos una función a cada uno. Usaremos, siguiendo una metodología reciente en este blog, funciones que nos devuelvan los resultados en forma de string, para poder ver las soluciones, y no un simple SÍ o NO. En este primer caso usaremos esta función:

Function doblado$(n)

Dim i, j, k, m

Dim s$

 

m = 0

s = ""

For i = 1 To n / 2 ‘Llegamos a n/2 buscando un cateto

j = n – i ‘El otro posible cateto

k = i ^ 2 + j ^ 2 ‘Vemos si forman terna pitagórica

If escuad(k) Then m = m + 1: s = s + " ##" + Str$(i) + " " + Str$(j) + " " + Str$(Sqr(k)) ‘En caso afirmativo, incorporamos a la solución

Next i

If s = "" Then s = "NO" Else s = Str$(m) + s ‘Añadimos número de soluciones

doblado = s

End function

Si recorremos con esta función los primeros números, obtendremos las primeras soluciones, que ya publicamos en la entrada de hace doce años:

Como era de esperar, este listado ya está publicado en http://oeis.org/A118905:

7, 14, 17, 21, 23, 28, 31, 34, 35, 41, 42, 46, 47, 49, 51, 56, 62, 63, 68, 69, 70, 71, 73, 77, 79, 82, 84, 85, 89, 91, 92, 93, 94, 97, 98, 102, 103, 105, 112, 113, 115, 119, 123, 124, 126, 127, 133, 136, 137, 138, 140, 141, 142, 146, 147, 151, 153, 154, 155, 158, 161, 164, 167, 168, 170, 175, 178, 182, 184, 186, 187, 188

Hemos observado que el número 49 admite dos soluciones, (9, 40, 41) y (21, 28, 35). La primera terna es primitiva, pero la segunda no.

Podemos extraer los primeros números que presentan dos o más soluciones:

El máximo de soluciones de la tabla anterior ha sido 4, pero existen números con más ternas posibles. Por ejemplo, los números 833, 1127, 1519 y 1666 presentan siete.

Aquí deberemos parar un poco. Observando la tabla, es fácil ver que muchas ternas no son primitivas. Si solo nos interesan estas, en la función de más arriba, además de exigir que k = i ^ 2 + j ^ 2 sea un cuadrado, deberemos añadir que estos lados sean primos entre sí, o que su MCD sea 1. Podría quedar así:

Function doblado$(n)

Dim i, j, k, m, p

Dim s$

m = 0

s = ""

For i = 1 To n / 2

j = n - i

k = i ^ 2 + j ^ 2

If escuad(k) Then

p = Sqr(k)

If mcd(i, mcd(j, p)) = 1 Then m = m + 1: s = s + " ##" + Str$(i) + " " + Str$(j) + " " + Str$(p)

End If

Next i

If s = "" Then s = "NO" Else s = Str$(m) + s

doblado = s

End Function

Con esta modificación, obtenemos un listado más restringido:

También estas soluciones están ya publicadas en http://oeis.org/A120681 con distinto orden. En esa misma página se remite a una prueba de que los factores de los números de la lista (la mayoría son primos) tienen factores primos del tipo 8k+1 o 8k-1 (el desarrollo está en http://oeis.org/A001132)

La razón de esta propiedad es que estos números, al ser suma de catetos en una terna primitiva, se pueden escribir de la forma u²-v²+2uv, con u y v primos entre sí y uno de ellos par (ver, por ejemplo Wikipedia). Esto los convierte en soluciones de (u+v)²-2v²=k, es decir una ecuación del tipo x²-2y²=k.

La consideración anterior los convierte también en soluciones de diferencia de catetos, porque u²-v²-2uv=(u-v)²-2v²=2x²-y², es decir, la misma ecuación. Este hecho se refleja en

http://oeis.org/A058529.

Podemos hacer explícita esta equivalencia. Si una suma de catetos proviene de dos valores u y v, su equivalente como diferencia se basa en los valores u+2v, v. Es fácil verlo:

Suma de catetos: (u+v)²-2v²

Diferencia equivalente: (u+2v-v)²-2v²

Es fácil verificarlo con dos ejemplos:

7 es suma de catetos en la terna (3, 4, 5), que corresponde a u=2, v=1. Los valores para que sea diferencia son u+2v=4 y v=1, que forman la terna (2*4*1, 4²-1², 4²+1²,)=(8, 15, 17), en la que la diferencia de catetos es también 7.

Otro ejemplo: En la terna (5, 12, 13), u=3 y v=2 con suma de catetos 17

El equivalente es (7-2)²-2*2*2=17, que es diferencia de catetos en la terna (7²-2², 2*7*2, 7²+2²)=(45, 28, 53), y 45-28=17.

Doblado en hipotenusa y cateto

En lugar de exigir una suma de catetos podemos estar interesados en suma de hipotenusa y un cateto. Para ello bastará cambiar algún signo en los códigos de Excel y PARI y modificar las cotas de los datos. Puede quedar de esta forma:

Function doblado$(n)

Dim i, j, k, m, p

Dim s$

m = 0

s = ""

For i = 1 To n

j = n - i

If j < i And j > 0 Then ‘Acotamos el cateto

k = i ^ 2 - j ^ 2 ‘En lugar de sumar, restamos

If escuad(k) Then

p = Sqr(k)

If mcd(i, mcd(j, p)) = 1 Then m = m + 1: s = s + " ##" + Str$(i) + " " + Str$(j) + " " + Str$(p) ‘Seguimos buscando primitivas

End If

End If

Next i

If s = "" Then s = "NO" Else s = Str$(m) + s

doblado = s

End Function

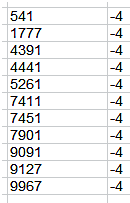
Al hacer uso del MCD indicamos que deseamos soluciones sobre ternas primitivas. Buscamos números con esta función y los primeros que encontramos son estos:

A primera vista comprobamos que existen muchas más soluciones múltiples. En la imagen ya aparece la primera con 6, el 169.

Otro hecho que se descubre es que todas las soluciones son  cuadrados o dobles de un cuadrado. La razón es sencilla, ya que al sumar una hipotenusa y un cateto en una terna primitiva, podemos encontrarnos con dos posibilidades:

Sumar u²+v²+2uv: En ese caso obtendríamos el cuadrado (u+v)²

Sumar u²+v²+u²-v², lo que os llevaría a 2u², el doble de un cuadrado.

Este razonamiento nos llevaría a pensar, como en el caso de los dos catetos, que estos números también serán diferencias entre hipotenusas y catetos, y en efecto, u²+v²-2uv es un cuadrado y u²+v²-u²+v² el doble de un cuadrado. Esta propiedad se refleja en http://oeis.org/A096033

Doblado en tres lados

El número que consideremos se podrá descomponer en tres lados, es decir, de forma que sea el perímetro de un triángulo rectángulo. Hay varias formas de plantearlo, pero por seguir los métodos de búsqueda anteriores, ampliamos las funciones usadas para que admitan una variable más. La función doblado quedaría así:

Function doblado$(n)

Dim i, j, k, m

Dim s$

m = 0

s = ""

For i = 1 To n - 2 'Llegamos a n-2 buscando la hipotenusa

For j = 1 To i - 1 'Primer cateto

If j < i Then

k = n - i - j 'El otro posible cateto

If i ^ 2 = j ^ 2 + k ^ 2 And k < j And k > 0 Then m = m + 1: s = s + " ##" + Str$(i) + " " + Str$(j) + " " + Str$(k) 'En caso afirmativo, incorporamos a la solución

End If

Next j

Next i

If s = "" Then s = "NO" Else s = Str$(m) + s 'Añadimos número de soluciones

doblado = s

End Function

En este caso, la búsqueda nos devolvería estos primeros resultados:

 Las soluciones se han publicado en  http://oeis.org/A010814

Si incorporamos la condición de que los tres lados, catetos e hipotenusa, sean primos entre sí, obtendremos las soluciones para ternas primitivas, que serán iguales a las anteriores o divisores de ellas, pues es sabido que el perímetro de una terna siempre es múltiplo de otro correspondiente a una primitiva. Lo hemos efectuado así, resultando:

Están publicados en http://oeis.org/A024364

Según los párrafos anteriores, la expresión de estos resultados vendrá dada por u²+v²+u²-v²+2uv=2u²+2uv=2u(u+v), donde u y u+v son primos entre sí. Por ello, si u es par, o lo es u+v, la solución será un número múltiplo de 4, y solo de 2 en caso contrario.

Por ejemplo, en la terna (5, 4, 3), u=2, v=1, u²+v²=5, u²-v²=3 y 2uv=4, el perímetro es 12=5+4+3, y es múltiplo de 4 por ser u par.

Sin embargo, en la terna (13, 12, 5), u=3, v=2, u²+v²=13, u²-v²=5 y 2uv=12. En este caso, u es impar, y u+v también, lo que significa que el perímetro 30 es múltiplo de 2, pero no de 4.

A la vista de los resultados podría parecer que cada solución se corresponde con una sola terna primitiva, pero no es así, pues, por ejemplo, 1716 se corresponde con dos:

1716=725+627+364 y 725^2=627^2+364^2; MCD(725, 627, 364)=1

1716=773+748+195 y 773^2=748^2+195^2; MCD(773, 748, 195)=1

Se puede detectar esto mediante un algoritmo en PARI, similar a este:

for(u=2,30,for(v=1,29,if(gcd(u,v)==1&&(u+v)%2==1&&u>v,write("final.txt",2*u*(u+v)))))

Engendra las soluciones buscando los valores de u y v adecuados.

Vuelca la solución en un archivo, al que hemos dado el nombre de “final.txt”. Las soluciones se escribirán en columna, pero desordenadas. Habrá que copiarlas en una hoja de cálculo, ordenar la columna y detectar los duplicados. Es otra forma de actuar.

 

Medias de tres primos consecutivos

Puede ser interesante estudiar la media aritmética de tres números primos consecutivos. En algunos casos, coincide con el primo central, que en ese caso sería equilibrado. No es esto infrecuente, pues los primos pueden ser del tipo 4k+1 o 4k-1, y también 6k+1 y 6k-1, además de otras pautas. También puede ocurrir que la media sea un tipo especial de número, como cuadrado, triangular u oblongo. Organizaremos búsquedas ordenadas y, entre ellas aparecerán casos que ya estén estudiados o que presenten propiedades interesantes.

Primo equilibrado

Con cualquier lenguaje de programación bastará exigir que

(prevprime(n)+n+postprime(n)/3=n

Se entiende que prevprime y postprime son los primos adyacentes a n. En todos los lenguajes se usan palabras similares. En este blog usamos PRIMANT y PRIMPROX, para hojas de cálculo.

Así que nuestra función para detectar primos equilibrados será:

Function primoequil$(n)

Dim s$

s = ""

If esprimo(n) Then

If (primant(n) + n + primprox(n)) / 3 = n Then s = Str$(primant(n)) + " ; " + Str$(primprox(n))

End If

primoequil = s

End Function

Le hemos dado carácter de string para que recoja los dos primos adyacentes.

Los primeros primos de este tipo son

Junto a cada uno figuran sus dos primos contiguos. Podemos añadir las diferencias con el centro, para más información.

Estos números están publicados en http://oeis.org/A006562

5, 53, 157, 173, 211, 257, 263, 373, 563, 593, 607, 653, 733, 947, 977, 1103, 1123, 1187, 1223, 1367, 1511, 1747, 1753, 1907, 2287, 2417, 2677, 2903, 2963, 3307, 3313, 3637, 3733, 4013, 4409, 4457, 4597, 4657, 4691, 4993, 5107, 5113, 5303, 5387, 5393,…

En la tabla de arriba, salvo el caso especial de 3, 5 y 7, todas las diferencias son múltiplos de 6 ¿Será así siempre?

En este mismo blog ya se ha razonado la respuesta afirmativa:

Las diferencias, salvo en el 5, son múltiplos de 6. La razón es que a partir del 5 todos los primos son del tipo 6n+1 o 6n+5. En las ternas que se forman tienen que ser todos del mismo tipo, ya que si el primero es 6n+1 y el segundo 6m+5, el tercero tendría el tipo 6m+5+(6k+4)=6h+3, no primo. Igualmente, si el primero es tipo 6n+5 y el segundo 6m+1, el tercero sería 6m+1+(6h+2). Lo puedes ver con Z₆: Si el primero tuviera resto 1 y el último resto 5, el promedio presentaría resto 3 y no sería primo. Igual con los otros casos.

https://hojaynumeros.blogspot.com/2015/07/formas-de-ser-un-numero-equilibrado-3.html

Por ejemplo, el primer primo que es media entre su anterior y posterior con diferencia 30 es 69623, que forma la progresión (69593, 69623, 69653)

Se ha conjeturado que existen infinitos primos equilibrados.

Desviaciones respecto al equilibrio

Si el primo central no es equilibrado, la media será mayor o menor que él, se desviará una “distancia” o diferencia. Salvo con el 2, siempre será par.

Podemos introducir esa distancia como parámetro en la función anterior:

Function primoequil(n, d)

Dim s, m

s = 0

If esprimo(n) Then

m = (primant(n) + n + primprox(n)) / 3 - n

If m = d Then s = m

End If

primoequil = s

End Function

Tal como está planteado, se desecharán las medias que no sean enteras, y el resultado será 0. Así que esta función devuelve un cero si no se da la diferencia dada, o esa diferencia si es válida. Por ejemplo, con ella hemos encontrado los primeros números en los que la media sobrepasa al primo central en 2 unidades:

No abundan las diferencias grandes: el número 5749 es el primero que presenta una diferencia de 8, porque la media es 5757. De igual manera, 15823 es el primero que presenta diferencia 10. Estos son los siguientes:

40289         d=16

45439         d=12

Podíamos buscar diferencias negativas:

Estos son los primeros primos con diferencia -4 (para ello hay que cambiar la declaración de variables a integer)

Media triangular

Podemos ahora investigar cómo son las medias entre tres números primos consecutivos, de qué tipo son. Las más interesantes son las de tipo polinómico, como triangulares, cuadradas y cúbicas. Recorreremos estos tres tipos abordando la búsqueda desde dos puntos de vista. Por un lado nos basaremos en los tres primos consecutivos, y, por otro, en los valores de N en los que se basan las fórmulas polinómicas.

Comenzamos con medias triangulares. Elegimos primos, y le calculamos la media de ellos con los dos siguientes. Si es triangular, la aceptamos. Usaremos PARI porque los números a manejar serán grandes.

El criterio para saber si un número es triangular es el conocido de que 8*n+1 sea cuadrado. De esta forma, la búsqueda queda así en PARI:

18713, 27253, 35227, 45433, 138587, 251677, 283861, 425489, 462221, 463189, 486583, 634493, 694409, 826211, 943231, 1103341, 1163557, 1181927, 1214453, 1282387, 1462891, 1509439, 1925681, 1931569,…

(Publicados en http://oeis.org/A226150)

Hemos usado aquí, en la web de PARI/GP https://pari.math.u-bordeaux.fr/gp.html un código mucho más simple que en la página enlazada:

ok(n)={my(m=nextprime(n+1),p=nextprime(m+1),r=(n+m+p)/3);isprime(n)&&issquare(8*r+1)}

for(i=2,2*10^6,if(ok(i),print1(i,", ")))

El otro procedimiento consiste en ir recorriendo los números triangulares n(n+1)/2 y detectar los primos más cercanos consecutivos. Como vimos en la primera parte de este estudio, la media de tres primos puede caer a la derecha o a la izquierda del central, por lo que esa detección se ha de efectuar dos veces. En este listado para Excel se comprende bien:

Function media_tres_prim(n)

Dim a, p, q, r, s, u, v, m

m = 0

a = n * (n + 1) / 2 ‘Se construye el número triangular

p = primprox(a): q = primprox(p): r = primant(a): s = primant(r)

u = (p + q + r) / 3: v = (s + r + p) / 3’Se estudian dos posibles medias

If u = a Then m = r ‘La media queda a la derecha

If v = a Then m = s ‘O a la izquierda

media_tres_prim = m

End Function

De una forma bastante rápida se reproduce el listado anterior y, además, nos devuelve los órdenes N de los números triangulares

Se comprende que es un método mucho más eficiente. Los números de la primera columna están publicados en http://oeis.org/A226147

 

Media cuadrada

Para encontrar casos con media cuadrada, bastará cambiar n(n+1)/2 por n^2 en Excel y 8*n+1 por n en PARI

En Excel nos resultarían:

 

Las bases de la primera columna están publicadas en http://oeis.org/A226146

En PARI, el primer primo resulta así:

ok(n)={my(m=nextprime(n+1),p=nextprime(m+1),r=(n+m+p)/3);isprime(n)&&issquare(r)}

for(i=2,1600000,if(ok(i),print1(i,", ")))

Simplemente hemos sustituido issquare(8*r+1) por issquare(m)

Media cúbica

Cambiando n^2 o n*(n+1)/2 en la función de arriba por n^3, resultan las bases y los primos iniciales de la terna para este caso:

53      148867

131   2248069

179   5735291

219   10503443

227   11697073

419   73560043

489   116930119

633   253636087

733   393832819

913   761048471

925   791453099

1021 1064332237

1223 1829276531

1247 1939096199

1263 2014698431

Y su código en PARI:

ok(n)={my(m=nextprime(n+1),p=nextprime(m+1),r=(n+m+p)/3);isprime(n)&&ispower(r,3)}

for(i=2,10^7,if(ok(i),print1(i,", ")))

Por terminar las búsquedas, nos quedamos con las potencias cuartas:

Cuarta potencia

7        2393

35      1500613

69      22667111

85      52200611

91      68574943

117   187388689

 

Queda a los lectores el reto de adaptar el código para este caso y probar otros números poligonales.

Regresos 3: Números intocables

Hoy regresamos a la fecha del 10 de junio de 2011, en la que publicamos la entrada “Cribas y barridos 1. Números intocables”. La primera parte trata del uso de las hojas de cálculo para cribar números según sus propiedades. Ahora nos interesa más un ejemplo concreto que se usó en ese estudio, el de los números intocables.

Se llaman así a aquellos números que no pueden ser el resultado de la suma de las partes alícuotas de otro número, es decir, de la suma de sus divisores propios. Por ejemplo, el 88 no coincide con el resultado de sumar los divisores propios de ningún número natural. Si efectuamos un barrido de los N primeros números y anotamos el resultado de esa suma, ningún resultado coincidirá con 88.

Los primeros números intocables son 2, 5, 52, 88, 96, 120, 124, 146, 162, 188, 206, 210, 216, 238, 246, 248, 262, 268, 276, 288, … http://oeis.org/A005114

Puedes aprender algo sobre estos números en la Red. Por ejemplo en

 http://mathworld.wolfram.com/UntouchableNumber.html,

No dan mucho de sí. Se aprenden sus propiedades en pocos minutos.

Para saber si un número es intocable o no, necesitaremos evaluar la suma de divisores propios de cualquier número (o partes alícuotas). Con una búsqueda exhaustiva podemos construir la función alícuota:

public function alicuota(n)

dim i,s

s=0

 

for i=1 to n/2 ‘El divisor propio máximo posible es n/2

if n/i=n\i then s=s+i ‘Si encuentro un divisor propio, lo sumo

next i

alicuota=s

End function

Esta función recorre los posibles divisores propios, con la prueba n/i=n\i, que equivale a afirmar que el cociente n/i es entero y que por tanto i divide a n. El resto se entiende fácilmente.

Si se dispone de la función SIGMA, es claro que es más sencillo el uso de ALICUOTA(N)=SIGMA(N)-N

Es lo que ocurre en el lenguaje PARI, que podemos usar sigma(n)-n. En este blog también puedes encontrar la función SIGMA para Excel o Calc.

Función de búsqueda

Si deseamos saber si un número es intocable o no, deberemos recorrer “muchos” números consecutivos y comparar su función ALICUOTA o SIGMA(N)-N con el número dado, pero el problema radica en cuántos son “muchos”. En OEIS usan la cota (n-1)^2, basándose en la desigualdad s(n)-n >= sqrt(n)+1 para números compuestos. Así lo haremos aquí. Al final de la entrada esbozamos una demostración de esta desigualdad.

Con esta cota, es fácil encontrar (pero puede que muy lento) si un número es intocable o no:

Esta puede ser la función:

 

Function intocable(n) As Boolean

Dim i

Dim m As Boolean

 

m = True ‘Suponemos que sí es intocable

i = 1

While i <= (n - 1) ^ 2 And m ‘Recorremos casos hasta (n-1)^2

If fsigma(i, 1) - i = n Then m = False ‘Si n es sigma, no es intocable

i = i + 1

Wend

intocable = m

End Function

Con esta función es fácil organizar un bucle de búsqueda en Excel, con el mismo resultado que el publicado en OEIS:

Este proceso tiene fácil traducción al lenguaje PARI:

intocable(n)={my(m=1,i=1);while(i<=(n-1)^2&&m==1,if(sigma(i)-i==n,m=0);i+=1);m}

for(m=2,1000,if(intocable(m),print1(m,", ")))

Con este código obtenemos los intocables inferiores a 1000

Se conjetura que el único intocable impar es el 5. Se ha demostrado que sería cierta si también lo es la de Goldbach, por lo que es, por ahora, un problema abierto. Si fuera cierto, los únicos primos intocables serían 2 y 5.

Ya afirmábamos en este blog hace 12 años que estos números no presentan muchas propiedades. Además de en  http://oeis.org/A005114 puedes buscar “untouchable numbers” en la Red.

Algunos tipos de intocables

Nosotros ahora nos dedicaremos a tipos especiales de intocables. Ya sabemos que primos solo están 2 y 5, y que impar solo el 5, y se puede demostrar que no habrá números perfectos, amigos o iguales a un primo más la unidad, pero, por ejemplo, ¿habrá cuadrados o triangulares? Adjuntamos a continuación algún resultado:

Triangulares: Si añadimos en PARI la condición issquare(8*m+1), que es la que detecta triangulares, encontramos que sí existen de ese tipo. Estos son los primeros triangulares intocables:

120, 210, 276, 406

Como el proceso es lento, nos basta con saber que existen esos cuatro.

Oblongos: Con la condición issquare(4*m+1) descubriremos oblongos:

También existen, y los primeros son:

2, 210, 306, 342, 552, 756

Cuadrados: Existen al menos tres: 324, 576 y 784

Otra posible definición

Ya planteábamos esta pregunta en la anterior entrada sobre estos números:

¿Qué ocurriría si exigiéramos que no coincidieran con la suma de divisores propios, sino con la suma de todos (función SIGMA)? Nos daría una lista (más numerosa) de números intocables de otro tipo.

Si adaptamos lo anterior eliminando el restar el número de su sigma, efectivamente, resultan tantos números que la cuestión pierde interés:

2, 5, 9, 10, 11, 16, 17, 19, 21, 22, 23, 25, 26, 27, 29, 33, 34, 35, 37, 41, 43, 45, 46, 47, 49, 50,…

Los tienes estudiados en http://oeis.org/A007369

 

ANEXO

Demostración de s(n)-n >= sqrt(n)+1 para números compuestos

Nos basamos en cualquiera de estas dos fórmulas equivalentes para s(n)

En ambas, p representa a los factores primos y e a sus exponentes.

Lo efectuaremos por fases. Por comodidad tipográfica, representaremos la raíz cuadrada como sqrt

(1) En los semiprimos:

(1a) Si n es un cuadrado, n=p², con p primo, s(n)=1+p+p²,(ver las fórmulas de s(n)) luego s(n)-n=1+p=1+sqrt(n). Se cumple con igualdad.

(1b) Si n no es cuadrado, n=ab, con a distinto de b, y s(n)=(1+a)(1+b)=1+a+b+ab, luego

s(n)-n=1+a+b=1+2(a+b)/2>1+2sqrt(ab)>1+sqrt(n)

Nos hemos basado en que la media aritmética (a+b)/2 es mayor que la geométrica sqrt(ab)

(2) Por inducción:

Si la propiedad es verdadera para dos factores, bastará estudiar qué ocurre cuando se agrega un nuevo factor primo.

Sea n1=n*a, con n compuesto. Consideremos dos casos, que a sea ya un factor de n o que sea nuevo.

(2a) Si a no es factor de n, s(n1)=s(n)*(1+a), por ser una función multiplicativa. Ahora, si se cumple la desigualdad para n, tendremos;

s(n1)=s(n)*(1+a)>(1+sqrt(n))*sqrt(a)sqrt(a)>1+sqrt(n*a)

(3b) Si a es factor de n, quedaría, siendo e su exponente en n,

s(n1)=s(n)(a^e+1-1)/(a^e-1) (cambia un numerador por otro en la primera fórmula)

(a^e+1-1)=(a*a^e-a+a-1)=a(a^e-1)+a-1,

s(n1)=s(n)(a(a^e-1)+a-1)/(a^e-1)= s(n)*a+s(n)*(a-1)/(a^e-1)= s(n)*a+M*(a-1),siendo M un número natural (porque (a^e-1) divide a s(n). Así llegamos como en el caso 3a, que

s(n1)>1+sqrt(n)*sqrt(a)sqrt(a)>1+sqrt(n*a)