Reciben el nombre de números regulares o 5-lisos aquellos números naturales que son divisibles entre 2,3 y 5 y ningún otro factor primo. Presentan una factorización prima del tipo 2n3m5p. También puedes identificarlos como aquellos que son divisores de una potencia de 60 (¿por qué?)
Los tienes presentados en estas páginas
http://en.wikipedia.org/wiki/Regular_number
https://oeis.org/A051037
En esta última puedes consultar cuáles son
1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36, 40, 45, 48,…
Si se les añade el número 1 como primer elemento, forman la llamada sucesión de Hamming.
El mayor interés que presentan estos números es el estudio de la formación ordenada de la sucesión, formándola a partir de los elementos ya descubiertos. Esto último es importante, pues si no, bastaría con ir recorriendo los números naturales para quedarnos sólo con los del tipo 2n3m5p.
Los posibles algoritmos, como el de Dijkstra, se estudian frecuentemente en programación funcional, como puedes ver en esta página de José_A_Alonso.
Nosotros, como siempre en este blog, optaremos por un enfoque elemental, didáctico y ¡cómo no!, usando una hoja de cálculo.
Generación del siguiente número de Hamming
Una vez que tienes escritos los primeros números de la sucesión 1,2,3,4,5,6,8,…(veremos que en realidad sólo hay que escribir 1), para obtener el siguiente bastará multiplicar uno de ellos por 2,3 o 5, pero, ¿cuál? En la sucesión 1,2,3,4,5,6,8,… no me sirve multiplicar por 2 el número 3, porque me daría 6 que ya lo tengo. Sí me convendría multiplicar por 2 el 5, con lo que obtendría el 10, o al revés, multiplicar 5 por 2. Esto no tiene nada de sistemático, por lo que deberemos ordenarlo un poco:
Dada una sucesión de Hamming con varios elementos, para formar el siguiente nos basaremos en estos criterios:
(1) Multiplicamos por 2, 3 o 5 todos los elementos que ya tenemos, y nos quedamos con el resultado menor que aún no esté incorporado a la sucesión. En el caso del ejemplo, el 9.
(2) Para guiarnos en este proceso, escribimos todos los números del tipo 2H, 3H y 5H, (representando H los números de Hamming que ya tenemos) en tres columnas.
H 2H 3H 5H
1 2 3 5
2 4 6 10
3 6 9 15
4 8 12 20
5 10 15 25
6 12 18 30
8 16 24 40
(3) En cada columna señalamos aquel número que cumple que todos los de arriba no superan el número que ya tenemos (8) y él es el primero que sí lo sobrepasaría.
En la siguiente tabla los tienes señalados en este caso.
H 2H 3H 5H
1 2 3 5
2 4 6 10
3 6 9 15
4 8 12 20
5 10 15 25
6 12 18 30
8 16 24 40
(4) Por último, de los tres candidatos elegimos el menor, 9, y ese será el siguiente elemento de la sucesión de Hamming.
Reiteramos estas operaciones y los obtendremos todos de forma ordenada. Este procedimiento tiene la ventaja de que una vez elegido un número de la columna quedan desechados los anteriores, por lo que es posible mantener unos punteros que nos indiquen por dónde vamos.
El algoritmo con hoja de cálculo
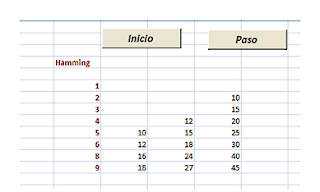
Podemos traducirlo a hoja de cálculo. Lo hemos intentado sin usar macros, pero aparecían referencias circulares muy molestas, por lo que hemos acudido al uso de rutinas y botones. Se inicia el proceso con el botón Inicio, que escribe el primer término 1 y sus tres múltiplos 2,3 y 5.
Después, cada vez que pulsemos sobre el botón Paso se irán eligiendo los múltiplos adecuados desechando los anteriores y los iguales. En la imagen puedes ver el estado del proceso después de obtener el 9:
Se han dejado en blanco los múltiplos usados. La hoja elige después el mínimo (sería 10), elimina sus iguales, lo incorpora a la lista, crea sus múltiplos y borra los innecesarios.
El cómo lo consigue lo podrás estudiar descargando la hoja en Excel desde
http://hojamat.es/blog/hamming.xlsm
(A OpenOffice lo tenemos en la nevera hasta ver qué pasa con él, y de LibreOffice estamos esperando la nueva versión)
Estudio mediante funciones
Para ver si un número es regular o 5-liso bastaría con esta definición de función:
Public Function es_regular(n) As Boolean
Dim nn
nn = n
While nn = 2 * Int(nn / 2): nn = nn / 2: Wend
While nn = 3 * Int(nn / 3): nn = nn / 3: Wend
While nn = 5 * Int(nn / 5): nn = nn / 5: Wend
If nn = 1 Then es_regular = True Else es_regular = False
End Function
Observa cómo lo detecta: mientras el número sea par, lo va dividiendo entre 2, con lo que al final deja de serlo. Mientras sea múltiplo de 3 y de 5 también va dividiendo. Si el número es regular se agotarán todos los factores y quedará sólo un 1 y el valor de la función será VERDADERO. Si no es regular es porque o no se puede dividir entre 2,3 o 5, o al final del proceso queda un factor mayor que 1, y la función devuelve FALSO.
Con esta función puedes iniciar la sucesión de Hamming en el punto que desees. Basta ir recorriendo números y eligiendo los que sean regulares. También es muy sencillo usar la función proximo_regular:
Public Function proximo_regular(n)
Dim p
p = n + 1
While Not es_regular(p): p = p + 1: Wend
proximo_regular = p
End Function
Con esta función puedes descubrir, por ejemplo, que el primer regular de siete cifras es 1012500.