Sumas del tipo m+n+mn

Como en otras ocasiones, cualquier comentario o reto aparecido en las redes sociales nos sirve de excusa para emprender un estudio. Hoy nos dedicaremos al número de descomposiciones del tipo k=m+n+mn (m>0 y n>0) que puede presentar un número k. A efectos prácticos podemos suponer que n es mayor o igual a m.

El número 99, por ejemplo, admite cuatro descomposiciones:

99=3+24+3*24
99=4+19+4*19
99=9+9+9*9
99=1+49+1*49

Otros números tan populares como el 30 no admiten ninguna descomposición de este tipo.

¿De cuántas formas se puede descomponer un número determinado? Como en ocasiones similares, comenzaremos con procedimientos de “fuerza bruta”, para ir después refinando el estudio hasta llegar al planteamiento teórico.

Con el Basic de Excel y Calc

En primer lugar debemos considerar que el valor mínimo para m y n es 1, luego el valor máximo será:

Si k=m+n+mn y damos a m el valor 1, despejando n resulta:

K=1+n+n, luego n<=(k-1)/2 y este valor sería la cota para m y n. Por otra parte, al despejar n en general, n=(k-m)/(m+1), este valor ha de ser entero y mayor que m (si queremos evitar repeticiones). Con esto ya podemos construir un algoritmo para contar el número de descomposiciones de este tipo que presenta un número dado.

Public Function numsumamn(k)
Dim m, n,  p

p = 0 ‘Contador de éxitos
For m = 1 To (k - 1) / 2 ‘m recorre el rango desde 1 hasta la cota
n = (k - m) / (m + 1) ‘El valor de n se despeja respecto a m
If n >= m And n = Int(n) Then p = p + 1 ‘Si es entero y mayor o igual a m, vale
Next m
numsumamn = p
End Function

Con este algoritmo podemos confeccionar tablas para esta función. La siguiente corresponde a los 20 primeros números:

Vemos que, por ejemplo, el 15 debe descomponerse de dos formas. Aquí las tienes:

1+7+1*7=15; 3+3+3*3=15

Algoritmo con el lenguaje PARI

Este algoritmo se traduce con facilidad al lenguaje PARI:

numsumamn(k)=local(p=0);for(m=1,(k-1)/2,n=(k-m)/(m+1);if(n==truncate(n)&&n>=m,p+=1));p

Con él y una estructura repetitiva puedes encontrar un listado de enteros con un número de descomposiciones fijado. El siguiente código nos devuelve los primeros números que admiten tres descomposiciones:

numsumamn(k)=local(p=0);for(m=1,(k-1)/2,n=(k-m)/(m+1);if(n==truncate(n)&&n>=m,p+=1));p
for(i=1,200,if(numsumamn(i)==3,print1(i,", ")))

Veamos el caso del 55: 1+27+1*27=3+13+3*13=7+6+7*6=55

Se obtienen las tres descomposiciones previstas.

Puedes experimentar con estos algoritmos, aunque al final de la entrada aprenderás un método mucho más eficiente.

Comprobación con Cartesius

Nuestra hoja de cálculo Cartesius (http://www.hojamat.es/sindecimales/combinatoria/herramientas/herrcomb.htm#cartesius),que desarrolla productos cartesianos condicionados, nos puede servir para comprobar los valores de la función numsumamn. Como sabemos que la cota para m y n es (k-1)/2, (o k/2 para simplificar), bastará combinar los distintos valores de ambos y destacar tan solo aquellos en los que m+n+mn=k. Quedaría así en el caso de k=71:

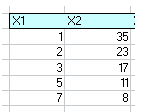
En primer lugar se fijan 2 elementos (serían m y n). Después se hacen recorrer el rango 1..36, que es la cota aproximada por exceso. La parte importante es la de exigir es x1+x2+x1*x2=71, según la cuestión que estamos resolviendo, y, por último, pedimos arreglos crecientes para eliminar duplicidades. Nos deberían dar 5 soluciones, según el valor de numsumamn(71), y, en efecto, los resultados son:

Lo podemos calcular: 1+35+1*35=36+35=71; 2+23+2*23=25+46=71; 3+17+3*17=20+51=71;
5+11+5*11=16+55=71; 7+8+7*8=15+56=71.

Puedes comprobar así cualquier valor de numsumamn(k)

Estudio teórico

Todo lo anterior se basa en un estudio “ingenuo”, en el que no se analiza la cuestión y sólo se pretende obtener resultados. Ahora veremos que los mismos tienen un fundamento teórico muy simple, que nos llevará a una fórmula para el número de descomposiciones del tipo m+n+mn=k

Basta darse cuenta de que la expresión estudiada equivale a (m+1)(n+1)-1. Por ejemplo, 2+35+2*35=37+70=107 es igual a (2+1)(35+1)-1=3*36-1=108-1=107.

Esto nos aclara la situación, porque el número de descomposiciones del tipo m+n+mn para un número k coincide con el de los pares de divisores cuyo producto es k+1. Así, las cuatro descomposiciones del número 99 (3+24+3*24, 4+19+4*19, 9+9+9*9, 1+49+1*49) coinciden con todos los pares de divisores (m+1)(n+1) del número k+1, en este caso 100. En efecto, los pares son: 2*50, que da lugar a 1+49+1*49, 4*25, que produce 3+24+3*24, 5*20 para 4+19+4*19 y 10*10, que se empareja con 9+9+9*9

El número de descomposiciones de k en expresiones m+n+mn coincide con el del número de pares de productos p*q=k+1 con p>1 y q>1.

El número de pares de este tipo está relacionado con la función TAU de k+1, que cuenta el número de divisores que posee k+1, y que tiene la expresión

En ella los valores de a₁, a₂,, a₃,,…son los exponentes de los factores primos de k+1. Si el valor de esa función es par, el número de productos p*q=k+1 será la mitad, y si es impar, la mitad más 1. A ese resultado habrá que restarle 1, porque el par 1*(k+1) no nos sirve. Así que quedaría:

Podemos comprobarlo con ejemplos concretos:

K=23; 24=2³*3; TAU(24)=(1+3)(1+1)=8; 8/2-1=3. Los pares válidos de divisores serán 2*12, 3*8, 4*6. Así que 23 debe admitir tres descomposiciones. Es fácil ver que son estas: 1+11+1*11, 2+7+2*7 y 3+5+3*5. Aquí tienes la comprobación con Cartesius:

En el caso de k+1=144, cuadrado perfecto, su función TAU es impar, lo que da sentido al hecho de que usemos la parte entera. Lo vemos:

K=143; k+1=144; 144=2⁴*3²; TAU(144)=(1+4)(1+2)=15; INT((15+1)/2)=8; 8-1=7.

Deberán aparecer 7 soluciones para los productos de divisores:2*72, 3*48, 4*36, 6*24, 8*18, 9*16, 12*12. Existirán, pues, 7 soluciones para nuestro problema. Las conseguimos con Cartesius:

Puedes irlas comprobando: 1+71+1*71=72+71=143; 2+47+2*47=49+94=143,…

Casos particulares

K+1 primo

Según lo anterior, los valores de k tales que k+1 sea primo, no admitirán la descomposición en m+n+mn.

Recuerda que entre los primeros 20 números tenemos (ver tabla de arriba) que 1, 2, 4, 6, 10, 12, 16, y 18 no admiten descomposiciones m+n+mn. Súmales una unidad y te resultarán los primeros primos: 2, 3, 5, 7, 11, 13,…

K+1 semiprimo

Los semiprimos poseen sólo dos factores primos, luego en ellos TAU=(1+1)(1+1)=4, y como 4/2-1=1, resultará que k sólo admitirá una descomposición. Es el caso de 3, 5, 8, 9,…en los que k+1 es semiprimo: 4=2*2, 6=2*3, 9=3*3, 10=2*5.

La propiedad contraria no es cierta, ya que 7 sólo admite la descomposición 1+3+1*3 y 8 no es semiprimo.

K+1 cuadrado

Si k+1 es cuadrado, k presentará una suma en la que m=n, como es fácil ver. Si k+1=p*p, k será igual a p-1+p-1+(p-1)(p-1). Es el caso, por ejemplo de 48, ya que 49=7*7 y 48=6+6+6*6.

Lo dejamos aquí. Este tipo de cuestiones elementales que dan lugar a experimentaciones sencillas se pueden abordar en las clases de Matemáticas de la Enseñanza Media. Sería divertido lanzar la idea en un trabajo por grupos y ver cada uno qué caminos emprende en sus búsquedas. No sería extraño que alguno diera con el truco del k+1.

Cartesius(6) – Particiones (2)

Condicionamientos sobre las particiones de un conjunto

En la entrada anterior de esta serie (http://hojaynumeros.blogspot.com.es/2017/06/cartesius-5-particiones-1.html) procedimos a crear particiones en un número, y en algunas condicionamos los sumandos, para que fueran primos, triangulares o cuadrados.  Ahora condicionaremos los resultados, y más adelante repasaremos los condicionamientos clásicos.

Condicionamientos sobre resultados

Las particiones de un número las hemos definido a partir de todas las sumas posibles, pero estas podrían ser condicionadas, en el sentido de suprimir algunas de ellas. Lo vemos con un ejemplo:

¿De cuántas formas podemos descomponer el número 7 en particiones con los dos sumandos menores iguales? 

Si no condicionamos los sumandos, existen, según vimos, 15 particiones. Al obligar a que los dos menores sean iguales, restringiremos ese número. Podemos plantearlo así:

XRANGO=7
XT=1..7
CRECIENTE
ES X1=X2
SUMA=7

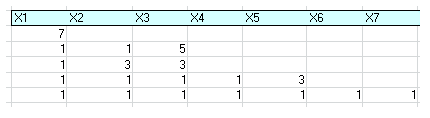
Es el mismo planteamiento de la entrada anterior sobre el tema de particiones, con el añadido ES X1=X2, que obliga a que los dos primeros sumandos sean iguales. Como hemos decidido que los arreglos sean crecientes, estos dos primeros serán también los menores. El resultado es:

Resultan ocho particiones en lugar de 15.

Podemos introducir muchos más condicionamientos: fijar la suma parcial de los tres menores o exigir que el tercer sumando sea mayor que el segundo, y otros parecidos.

Particiones condicionadas

Todos estos condicionamientos se suelen expresar como función así:
P(N/condicionamiento)
De esta forma, el anterior ejemplo se escribiría como P(7/x1=x2)

Otro ejemplo

Imaginemos que deseamos que el tercer sumando sea a su vez suma de los dos anteriores. Procederíamos así:

XRANGO=7
XT=1..7
CRECIENTE
ES X3=X1+X2
SUMA=7

Al desarrollar veríamos que es un ejemplo sin interés, porque sólo existe una suma así (siendo sumandos crecientes)

En efecto, si los valores iniciales son 1, 1, 2, ya no admiten para suma 7 nada más que un 3.

Condicionamientos clásicos

Ya vimos en entradas anteriores sobre particiones que históricamente se han planteado algunos condicionamientos especiales a las particiones. Los recorremos de nuevo:

Función de partición Pk(N) 

Es la misma función P(N) condicionada a que sólo intervenga un número K de sumandos:

Pk(N)= P(N / k sumandos): Particiones con un número k de sumandos fijado.
Con la hoja Cartesius es fácil programar esta función, ya que basta con definir XTOTAL=K, dejando el resto de condiciones igual.
Por ejemplo, evaluamos las particiones del número 12 en 4 sumandos, es decir p4(12):

xtotal=4 
xt=1..12 
creciente 
suma=12

Resultan 15 particiones.

Función de partición Q(N)

Como la anterior, cuenta el número de particiones, pero en este caso se exige que los sumandos sean todos distintos. Por ejemplo, el entero 7 admite las siguientes particiones como números distintos: 7 = 6+1 = 5+2 = 4+3 = 4+2+1, luego Q(7)=5

Euler demostró que esta función coincide con el número de particiones de n en partes impares. Lo veremos más adelante.

La programación de esta función se consigue añadiendo la condición NO REPITE, para que todos los sumandos sean iguales. En el caso del 7 podríamos escribir:

xrango=7
xt=1..7
suma=7
creciente
no repite

Tendríamos el resultado siguiente:

Sólo son posibles las cinco particiones.

Particiones en partes impares P(N/Impar)

Introducimos este condicionamiento porque da lugar a un resultado obtenido por Euler:

El número de particiones de un número en sumandos distintos coincide con el de particiones en sumandos impares

Con Cartesius el planteo se limita a exigir que los sumandos sean impares. Basta condicionar los sumandos como una sucesión del tipo 2*n-1:

Obtenemos cinco particiones, el mismo número que nos dio el de sumandos distintos.

Podíamos haber usado un filtro, para que los sumandos sean impares:

Resultaría más rápido que el planteamiento anterior. Por último, otra posibilidad es definir los sumandos como un conjunto:

También es más rápido.

En otra futura entrada seguiremos condicionando las particiones de un número.

Números figurados e interpolación polinómica

Las entradas sobre números piramidales publicadas en este blog contenían siempre una fórmula polinómica para expresar cada término de la sucesión. Por ello parece conveniente presentar un método general para la obtención de esas fórmulas. Disponemos para ello de la teoría de la interpolación polinómica, en la que elegiremos el método de Newton, y una hoja de cálculo que nos facilitará las cosas.

Teoría

Los conceptos y métodos de la interpolación polinómica los puedes encontrar en cualquier texto del primer ciclo de estudios universitarios. Todos se basan en el cálculo con diferencias sucesivas. En nuestro caso nos limitaremos a la suma de funciones enteras definidas sobre los primeros números naturales, lo que simplifica mucho los cálculos.

Por ejemplo, imaginemos que deseamos sumar los primeros números oblongos: 1*2, 2*3, 3*4, 4*5, 5*6,…o bien, 2, 6, 12, 20, 30,…Queremos obtener una expresión para 2+6+12+20+30+…

En las técnicas de interpolación que usaremos, la primera operación es la obtención de las diferencias sucesivas, es decir, diferencias entre los elementos, diferencias entre las diferencias, y así sucesivamente hasta (en el caso polinómico) que sean todas iguales. Lo intentamos con el ejemplo. En primer lugar encontramos las sumas parciales de oblongos: 2, 2+6=8, 2+6+12=20,…que serían 2, 8, 20, 40, 70, 112, 168, 240,…

Lo puedes organizar con una hoja de cálculo:

La siguiente imagen, tomada de nuestra hoja newton.xls, puedes entender muy bien el concepto de diferencias sucesivas. En primer lugar hemos escrito nuestra sucesión: 2, 8, 20, 40, 70, 112, 168,…Después hemos ido restando cada elemento con el siguiente: 6, 12, 20, 30, 42, 56,…(resultan ser los oblongos). A continuación hemos restado esas diferencias: 6, 8, 10, 12, 14,…entre sí, y al final en otra resta, hemos llegado a 2, 2, 2,…Esa es la señal de que esos números siguen una expresión polinómica, el que las diferencias se hagan iguales y las siguientes nulas.

Como aquí las diferencias constantes se alcanzan en tres pasos, la fórmula que buscamos será un polinomio de tercer grado. Lo repasamos en teoría:

Fórmula de interpolación de Newton

Cuando en un proceso se llega a diferencias constantes, sabemos que es posible expresar la sucesión dada mediante un polinomio dependiente del número de orden. La fórmula hallada por Newton es algo compleja en el caso general, en el que hay que usar diferencias divididas, pero se simplifica bastante en el caso de un polinomio aplicado al conjunto 1, 2, 3, 4,…Sería esta:

En ella a₀ es el primer término, d₁ la primera diferencia, d₂ la primera de las segundas diferencias, y así sucesivamente. En nuestro caso sería:

P(x)=2+6(x-1)+6(x-1)(x-2)/2!+2(x-1)(x-2)(x-3)/3!

Reduciendo a común denominador y simplificando:

Lo hemos comprobado con la hoja de cálculo. Observa la coincidencia de los valores en rojo:

Como ves, lo que es más complicado es la simplificación, pero el método es simple: encontrar diferencias sucesivas hasta que se estabilicen, y aplicar la fórmula de interpolación simplificada para los puntos de apoyo 1, 2, 3, 4,…
Todo esto puedes reproducirlo con nuestra hoja de cálculo newton, que puedes descargar desde

http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#newton

Recuerda que sólo te vale para sumas definidas sobre los primeros naturales.

Basta escribir los valores de la sucesión en la segunda fila

y leer los coeficientes (en forma de fracción) más abajo:

Es fácil de interpretar (de derecha a izquierda): 2/1 es el coeficiente de 1, 6/1 el de (x-1), 6/2 para (x-1)(x-2) y, finalmente, 2/6 para (x-1)(x-2)(x-3). Después vendría la simplificación, pero si quieres ahorrártela, la hoja dispone del cálculo para un valor concreto. Por ejemplo, ¿cuánto suman los diez primeros oblongos?

Para ello dispones de las celdas adecuadas

La respuesta es 440. Hay que advertir que puede producir pequeños errores para índices grandes, por lo que se aconseja comprobar.

Si deseas evitarte la simplificación puedes acudir a un CAS. Nosotros hemos usado wxMaxima para obtener el resultado previsto:

Otro paso sería el intentar, si es posible, buscar una interpretación al resultado obtenido. En nuestro caso es fácil ver que, para x mayor o igual a 3, se reduce a

Este proceso se puede repetir para números poligonales, piramidales o poligonales centrados (y otros similares que nos inventemos), porque todos se basan en sus definiciones en la acumulación de sumas, lo que garantiza que la fórmula buscada es de tipo poligonal.

Otro ejemplo

Sabemos que los números piramidales triangulares se construyen sumando los triangulares, y estos, a su vez, acumulando los naturales. Con un sencillo esquema los identificamos:

Luego los primeros piramidales son 1, 4, 10, 20,….Los volcamos en la hoja newton para descubrir sus diferencias y los coeficientes de interpolación:

Las diferencias son 1, 3, 3 y 1, y con ellas se construyen los coeficientes 1/1, 3/1, 3/2 y 1/6. Rellenamos la fórmula de interpolación y queda:

P(x)=1+3(x-1)+3/2(x-1)(x-2)+1/6(x-1)(x-2)(x-3)

Simplificamos con wxMaxima:

Coincide con la que se obtuvo en la entrada correspondiente a los números tetragonales (o piramidales triangulares)

http://hojaynumeros.blogspot.com.es/2017/04/numeros-piramidales-2-tetraedros.html

Con lo aprendido hoy estamos preparados para saltar a la cuarta o quinta dimensión, y sumar números piramidales consecutivos. Lo dejamos para otra entrada.