Simulaciones - Distribución uniforme (1/2)

Iniciamos hoy una serie, que nos tomaremos con calma, sobre simulaciones elementales de variables aleatorias. Nos basaremos en las prácticas de nuestro curso de Estadística, (http://www.hojamat.es/estadistica/iniestad.htm) adaptándolas al formato de un blog. Usaremos nuestro Simulador implementado para hojas de cálculo, el cual puede sufrir cambios a lo largo de la serie, por lo que se aconseja su recarga en caso de duda.

Comenzaremos con la distribución uniforme. Si no tienes claro el concepto puedes acudir a la Teoría correspondiente

(http://www.hojamat.es/estadistica/tema6/teoria/teoria6.pdf).

Por ahora te basta con la idea de que representa experimentos aleatorios en los que todos los elementos presentan una misma probabilidad de ocurrir, como tiradas de dados o las loterías. Se suele distinguir entre distribución uniforme discreta, cuando sólo existe un número finito de posibilidades (dados o monedas), o continua, cuando pueden aparecer infinitos sucesos, o al menos, tantos, que sea preferible tratarlos como infinitos.


Distribución uniforme discreta

En ella se trabaja sobre un conjunto finito de n elementos con la hipótesis de que todos ellos poseen la misma probabilidad de aparecer, que será, por tanto, 1/n. Un ejemplo es el de una tirada de dados. La distribución uniforme más útil es aquella en la que el conjunto está formado por los números comprendidos entre a y b ambos inclusive. En los dados a=1 y b=6
.
Puedes consultar en cualquier manual los valores de los principales estadísticos de esta distribución.

Media:

Varianza:

En el caso de las tiradas de dados m=3,5 y var=35/12=2,92 y su desviación típica 1,7321.

Podemos comprobar estos valores mediante nuestro simulador, alojado en estas direcciones:

http://www.hojamat.es/estadistica/tema1/open/simulador.ods (versión LibreOffice Calc)

http://www.hojamat.es/estadistica/tema1/open/simulador.xlsm (versión Excel)

Contiene dos hojas, la de criterios y simulación y la de los estadísticos. La mejor forma de aprender su funcionamiento es proceder a la primera simulación.

Deseamos saber si con 1000 tiradas de dados su media y varianza se acercan suficientemente a la teoría. Para ello, en la primera página del simulador concretamos lo siguiente:

Cinco repeticiones de 200 filas y una columna, para que se acumulen 1000 tiradas, mínimo=1 y máximo=6. Como criterios, “Uniforme”, “Entero”, para que la distribución sea discreta, y “Máximo-Mínimo”. También es conveniente fijar, unas celdas más abajo, el número de intervalos en 6. El resto de parámetros se puede ignorar. Con ello, al dar al botón Simulador obtendrás los resultados en la siguiente hoja de Estadísticos. En nuestro caso serían:

Se ha obtenido una aproximación apreciable. La herramienta también nos proporciona la asimetría y la kurtosis, pero prescindimos de ellas en esta simulación. A la derecha puedes observar la tabla de frecuencias y el diagrama de barras, que presenta una uniformidad de alturas bastante aceptable para el número de simulaciones que hemos fijado:

Como ya sabrás, es probable que, si aumentamos el número de repeticiones, el ajuste mejore, pero no lo des por seguro, que sólo existe una probabilidad. Si aumentamos a 50 repeticiones obtenemos:

Ha mejorado bastante el ajuste. En general, las simulaciones comienzan a ser útiles si las repites miles de veces. Con unas pocas no son útiles.


Distribución uniforme continua

En esta modalidad los datos se distribuyen de forma continua (en la práctica, con todos los decimales que deseemos) entre dos extremos a y b. Prácticamente no hay ejemplos en la vida diaria de distribuciones uniformes, ya que son más frecuentes otras, como la normal.  Suelen aparecer en experimentos diseñados o en instrumentos creados por nosotros, como puede ser el movimiento de las manecillas de un reloj, que recorre de manera uniforme toda la circunferencia.

Un ejemplo de distribución uniforme continua es el experimento de calcular π mediante simulación (método de Montecarlo). Consiste en simular dos coordenadas X e Y de manera uniforme entre 0 y 1 y contar aquellos pares en los que X^2+Y^2<1. De esa forma, su frecuencia relativa deberá ser ?/4=0,7854 aproximadamente. En la imagen sería como contar todos los puntos que caen dentro de la zona sombreada.

Lo organizaremos así:

Planteamos los criterios contenidos en la imagen:

Tomamos 500 filas y dos columnas (que representarán X e Y). No planteamos repeticiones porque añadiremos una columna nueva a la simulación. Concretamos un mínimo de 0 y un máximo de 1. En los restantes criterios elegimos “Uniforme”, “Decimal” (por ser continua) y “Máximo-Mínimo”.

Con ello obtenemos dos columnas de 500 valores de X e Y. Ahora, en una columna paralela, por ejemplo comenzando en J5, escribimos =SI(G5^2+H5^2<1;1;0). Esto significa que obtendremos un 1 si el punto (X,Y) pertenece al sector circular sombreado, y 0 si está fuera. Extendemos esa fórmula hacia abajo hasta abarcar los 500 valores:

Ahora basta sumar esa columna nueva y deberemos obtener un valor próximo a 500π/4≈393. Esto no se suele obtener en una simulación con tan pocos datos. En nuestro caso se ha obtenido 389. Podemos repetir el trabajo (de forma manual) varias veces y encontrar la media de resultados. Aquí tienes un ejemplo, con 7 repeticiones o 3500 casos:

389, 408, 383, 389, 392, 386, 384

Sumo y obtengo 2731, divido entre 3500 (para encontrar la frecuencia relativa) y multiplico por 4 para aproximar a ?: 2731/3500*4=3,1211. No es una extraordinaria aproximación a π, pero resulta aceptable si tenemos en cuenta las herramientas utilizadas.

Análisis de intervalos

En una de las actualizaciones del Simulador hemos añadido una simulación entre intervalos. En el caso de la distribución uniforme nos servirá para analizar la igualdad aproximada de las frecuencias en intervalos de igual longitud.

En la segunda hoja Estadísticos figura una tabla y un botón para obtener frecuencias f entre dos extremos a y b . Estos extremos se consideran alcanzables, por lo que en las distribuciones discretas estarán incluidos. En la última fila se calcula la frecuencia relativa h. Sólo se puede usar para tres columnas o menos. Basta fijar los extremos en cada columna, pulsar el botón Intervalos y comparar resultados.

La imagen corresponde a una simulación uniforme continua entre 10 y 20, con tres columnas. En cada una de ellas hemos fijado extremos con una diferencia de 4, con lo que las tres frecuencias relativas se acercan a 0,4.

Escaladas de Conway

El año pasado, 2017, se notificó que una conjetura de Conway, conocida como “escalada a un primo” había resultado ser falsa. Tienes la noticia, comentarios y contraejemplos en estos dos blogs:

http://francis.naukas.com/2017/06/14/contraejemplo-a-una-conjetura-de-conway-sobre-los-primos/

https://www.gaussianos.com/la-conjetura-de-la-escalada-hasta-un-primo/

Si los has leído (y si no, te bastará con mi explicación) entenderás que el proceso que propone Conway es el de descomponer el número en sus factores primos agrupados con exponentes y ordenados en orden creciente, como 144=2⁴*3², y después escribir seguidos y mezclados bases y exponentes de las potencias resultantes (2432).

Si un número primo está elevado a la unidad, esta se ignora y no se añade al nuevo número.

Si llamamos f(n) a esa función obtendremos:

f(144)=2432

La idea de Conway es la de ir reiterando esta función hasta llegar a un número primo p, en el que es evidente que f(p)=p, dando fin al proceso.
En el caso del 144:

F(144)=2432, f(2432)=2719, que es primo y con él termina el proceso.

Los dos blogs citados te darán más detalles. Nuestro objetivo en esta entrada es conseguir el algoritmo con el Visual Basic de las hojas de cálculo. Es, por tanto un interés operativo más que matemático.

Función fconway(n)

A continuación se inserta el listado para hoja de cálculo de la función de Conway, pero antes hay que acudir a la función ajusta(n), que elimina del número n los espacios en blanco que Excel o Calc añaden a los números naturales. Su código es el siguiente:

Function ajusta$(a)
Dim d$

d$ = Str$(a) ‘Convierte el número en un string
While Left$(d$, 1) = " " ‘Mientras esté precedido de un espacio, este se elimina
d$ = Right$(d$, Len(d$) - 1) ‘Se corta el string desde su segundo carácter
Wend
ajusta$ = d$
End Function 

Una vez contamos con esta función, se tratará ahora de descomponer el número en factores y concatenar factores primos y exponentes, eliminando aquellos iguales a la unidad. Puede ser así:

Public Function fconway(n)

Dim primo(20), expo(20), numomega ‘Reservamos 20 memorias para primos y exponentes
Dim s$
Dim f, a, e, i


a = n ‘Recibimos n en la variable a
f = 2: i = 0: numomega = 0 ‘numomega es el número de primos
While f * f <= a ‘Vamos extrayendo primos hasta la raíz cuadrada de a
e = 0
While a / f = Int(a / f)
e = e + 1 ‘Se toma nota del exponente, que va creciendo
a = a / f ‘Se elimina el factor primo encontrado
Wend
If e > 0 Then ‘Se incorpora el nuevo primo con su exponente a las memorias
numomega = numomega + 1
primo(numomega) = f
expo(numomega) = e
End If
If f = 2 Then f = 3 Else f = f + 2 ‘Se avanza en posibles primos
Wend
If a > 1 Then ‘Se recoge el último primo
numomega = numomega + 1
primo(numomega) = a
expo(numomega) = 1
End If
s$ = "" ‘Construimos la concatenación de primos y exponentes mayores que 1
For i = 1 To numomega
s$ = s$ + ajusta(primo(i)) ‘Se incorpora el primo
If expo(i) > 1 Then s$ = s$ + ajusta(expo(i)) ‘Se añade el exponente si es mayor que 1
Next i
fconway = Val(s$) ‘Convertimos el string en número
End Function

Si escribimos un número cualquiera (en los blogs citados no se recomienda usar el 20) en una celda de Excel y tenemos implementada la función anterior (debes entrar en Programador – VisualBasic. Puedes consultar http://hojamat.es/guias/descubrir/htm/macros.pdf), podemos calcularla en la celda inferior, y después extenderla hacia abajo hasta que el resultado se repita o alcancemos una magnitud para la que Excel pasa a notación científica. Puedes ver algún ejemplo en la imagen:

En el primero, se alcanza el primo inmediatamente. En el segundo, al segundo intento, como ya vimos más arriba. El siguiente sobrepasa la capacidad de Excel, y el cuarto llega al primo en cinco pasos.

Podemos convertir este proceso en una función, pero si llegamos a los límites de Excel habrá que devolver un valor que lo indique, como podría ser el cero. Hemos diseñado esta:

Public Function finconway(n)
Dim a, b

a = 1: b = n ‘Usamos dos variables para cada iteración
While a <> b And a < 100000000000# And a > 0 ‘Límites de la iteración
a = b ‘Guardamos b en la variable a
b = fconway(b) ‘Avanzamos un paso en la iteración
If a >= 100000000000# Then a = 0 ‘Si el número es muy grande, lo hacemos cero
Wend
finconway = a
End Function

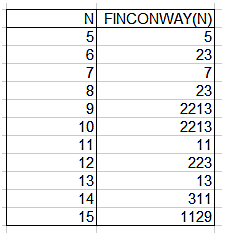
Con esta función se resuelve rápidamente el ascenso a primo. Aquí tienes los resultados desde 5 hasta 15, por ejemplo:

Esta función, aplicada al 542, devolvería un 0, ya que sobrepasa el límite de Excel para la escritura de todas las cifras. Este inconveniente se salva usando otro lenguaje. Hemos adaptado y completado la función en PARI incluida en la sucesión http://oeis.org/A080670 para definir la función finconway en ese lenguaje. Su código es:

fconway(n)=if(n>1, my(f=factor(n), s=""); for(i=1, #f~, s=Str(s, f[i, 1], if(f[i, 2]>1, f[i, 2], ""))); eval(s), 1)
finconway(n)=my(a=1,b=n);while(a<>b&&a>>0,a=b;b=fconway(b));a

Con ella es fácil reproducir los resultados de la tabla anterior:

Con el lenguaje PARI sí podemos encontrar el primo al que llegan las iteraciones con inicio en 542. Sería 131811420855589. En la imagen se puede observar cómo lo presenta PARI:

La conjetura

Si has leído las entradas de blog recomendadas más arriba, sabrás que existe un contraejemplo en el que la iteración no asciende a un primo, sino a un compuesto. Se trata del valor 13532385396179=13*532*3853*96179

Con nuestra función en PARI se detecta su invariancia en la iteración:

fconway(n)=if(n>1, my(f=factor(n), s=""); for(i=1, #f~, s=Str(s, f[i, 1], if(f[i, 2]>1, f[i, 2], ""))); eval(s), 1)
finconway(n)=my(a=1,b=n);while(a<>b&&a>>0,a=b;b=fconway(b));a
print(finconway(13532385396179))

En la imagen observamos que el resultado es el mismo valor:

Con esto terminamos, ya que el único objetivo era usar medios elementales para reproducir los ascensos a primo de Conway y el contraejemplo descubierto recientemente.

Acercamiento entre potencias

Se sabe que sólo existen dos potencias que se diferencien en una unidad, que son 8=2³ y 9=3². Sí pueden existir otros casos con diferencias mayores entre cuadrado y cubo. Vemos los primeros ejemplos:

Dif=2: 5²+2=3³
Dif:=3: 2²-3=1³
Dif=4: 2²+4=2³; 11²+4=5³
Dif=5 y 6: No hay ejemplos elementales
Dif=7: 1²+7=2³; 181²+7=32³
Dif=8: 3²-8=1³; 4²-8=2³; 312²-8=46³
Dif=9: 6²-9=3³; 15²-9=6³; 253²-9=40³
Dif=10: No hay ejemplos elementales.

Todos son casos particulares de la ecuación x²=y³+k, que necesita conocimientos profundas de Teoría de Números para su resolución. Por eso, aquí se usarán técnicas de búsqueda de soluciones en casos particulares.

Diferencias entre cuadrados y cubos

Podemos usar una función que mida el acercamiento a un cubo. Así, si se construye una lista de cuadrados, se podrán elegir aquellos que se diferencien de un cubo en un número dado. Así se han encontrado los ejemplos del párrafo anterior.

La función adecuada puede ser esta, que está diseñada para cualquier valor del exponente. Actúa sobre un número (que puede ser otra potencia), una diferencia dada y el exponente de la potencia. Al número le sumamos y restamos la diferencia dada, y con otra función, espotentipo, se averigua si es potencia perfecta o no.


Public function difepot(n,dife,ex1) as boolean
'para un número n ver si dista dife unidades de una potencia dada
‘Variables: n es el número, dife, la diferencia dada y ex1 el exponente de la potencia.

dim a,b
dim es as boolean

es=false ‘Declaramos que la función es falsa
a=n+dife ‘Buscamos la potencia “por arriba”
if espotentipo(a,ex1) then ‘Más abajo se explica esta función
es=true ‘Si es potencia, la diferencia es válida.
else
b=n-dife ‘Buscamos la potencia “por arriba y procedemos del mismo modo”
if b>0 then
If espotentipo(b,ex1) then es=true
end if
end if
difepot=es
end function

La función espotentipo busca si un número es potencia con un exponente dado. Actúa sobre el número y el exponente y devuelve VERDADERO o FALSO. Su código es el siguiente:

Public Function espotentipo(n, k) As Boolean
Dim m, i
Dim e As Boolean

m = Log(n) / k
m = Int(Exp(m)) ‘Mediante logaritmos, encuentra un posible valor para la base de la potencia
e = False
For i = m - 1 To m + 1 ‘Por si existen errores de redondeo, prueba con m, m+1 y m-1
If i ^ k = n Then e = True ‘Si con uno de ellos se reconstruye la potencia, es válido
Next i
espotentipo = e
End Function

Con estas dos funciones, bastará crear una lista de cuadrados y ver si alguno de ellos se diferencia de un cubo (mayor o menor que él) en una cantidad dada.  Por ejemplo, si construimos la lista de los veinte primeros cuadrados, veremos que al llegar al 14, su cuadrado se diferencia en 20 unidades del cubo de 6: 14²+20=6³.

Potencia más cercana

Podemos encontrar, para un número cualquiera, la potencia de cierto exponente que esté más cercana, y evaluar su diferencia. Para ello podemos usar esta otra función:

Public function difepot2(n,ex1)
'busca la potencia ex1 más cercana y devuelve la diferencia
dim p,q

p=int(n^(1/ex1))
dife=abs(n-p^ex1)
q=abs(n-(p+1)^ex1) ‘Busca la potencia si es menor o mayor. Ambas valen.
if q<dife then dife=q ‘Se queda con la diferencia menor.
difepot2=dife
end function

En esta tabla puedes observar las diferencias con el cubo más cercano. Se descubre que esos cubos son el 8 o el 27. Hasta el 17, el cubo más cercano es el 8, y a partir del 18, el 27.

Versión en PARI

Estas funciones de Excel no tienen mucha potencia de cálculo. Por eso, en algún momento usaremos sus versiones en PARI, cuyo código es el siguiente:

espotentipo(n,k)=local(m,i,es);m=log(n)/k;m=truncate(exp(m));es=0;for(i=m-1,m+1,if(i^k==n,es=1));es
difepot(n,ex1)=local(p,q,dife);p=truncate(n^(1/ex1));dife=abs(n-p^ex1);q=abs(n-(p+1)^ex1);if(q<=dife,dife=q);dife

Con el uso de ambas, hemos reproducido la tabla anterior entre el 10 y el 20:

Como ejemplo del uso de esta función, se inserta a continuación la tabla de diferencias entre cuadrado y cubo menores que 10 (y mayores que 0) para potencias interiores a 1000000:

Otras potencias

Diferencias mínimas entre cubo y cuarta potencia, dife<30:

Entre cuartas y quintas potencias, dife<50:

Así podemos seguir con otros casos. Terminamos con cubos y séptimas potencias:

Para terminar, agrupamos en una misma tabla diferencias menores que 10 en algunos casos. Hemos eliminado en la segunda potencia los valores 1 y 2, ya conocidos y triviales: