Frontera entre dos sumas equivalentes (2)

En la entrada anterior buscábamos números que separaran sumas equivalentes de cuadrados consecutivos. Ideamos tres algoritmos y comprobamos su equivalencia. En esta segunda entrada aplicaremos las ideas a otros tipos de números.

Sumas de triangulares

El número 17 cumple la propiedad que estamos estudiando si la aplicamos a números triangulares. En efecto, estas dos sumas de triangulares consecutivos son equivalentes, y sus órdenes están separados por el número 17:

T(14)+T(15)+T(16)=14*15/2+15*16/2+16*17/2=361

T(18)+T(19) =18*19/2+19*20/2=361

Podemos intentar buscar qué otros números naturales cumplen esta misma propiedad. En el primer y tercer algoritmo presentados en la entrada anterior, bastará sustituir las expresiones tipo j^2 por las de los triangulares j*(j+1)/2. Los dos algoritmos 1 y 3 coinciden en las soluciones:

 

Con la función SUMAFUN de uso propio podemos comprobar las soluciones para 122, que son 29 y 153:

sumafun(29;121;"X*(X+1)/2")=298561

sumafun(123;153;"X*(X+1)/2")=298561

Estos resultados coinciden con los correspondientes a la suma de oblongos, porque son sus dobles.

Sumas de números primos

En el caso de los números primos, es preferible exigir que el número frontera sea primo, pues, en caso contrario, aparecerían varios números consecutivos para una misma suma. Es cuestión de economía de resultados.

Adaptando convenientemente las funciones tipo “frontera” de hoja de cálculo llegaríamos a este listado:

Primo Valores de a y b

23      11 31

47      17 67

101   67 127

193   53 271

197   37 281

211   163 251

251   131 337

269   163 349

307   11 439

379   139 521

389   83 563

449   29 647

509   283 661

571   199 787

653   569 743

733   397 971

739   229 1033

743   643 829

769   131 1097

859   241 1217

883   11 1289    

Por ejemplo, el número 101 es primo y separa dos sumas iguales de consecutivos, que llegan hasta 67 por la parte inferior y a 127 por la superior. Lo hemos comprobado con esta tabla de Excel:

Suma de cubos

Sólo hemos encontrado (sin buscar demasiado, porque el proceso es lento) el ejemplo de 29, en el que la suma de cubos desde 4 hasta 28 coincide con la de los comprendidos entre 30 y 34. Lo puedes comprobar en esta tabla:

 

Con otros tipos de números

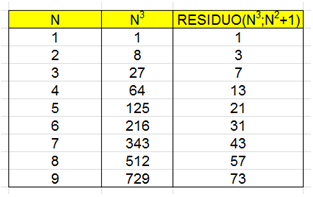
Si los sumandos los tomamos del tipo n²+1, sí existen soluciones:

Comprobamos, por ejemplo, el primero: las sumas desde 168 hasta 472 y desde 474 hasta 591, formadas por sumandos del tipo n²+1, han de ser iguales. Lo comprobamos con nuestra función SUMAFUN:

SUMAFUN(168;472;"X^2+1")=33596665

SUMAFUN(474;591;"X^2+1")=33596665

 

Sumas de valores de polinomios

Con estas técnicas podríamos extender el estudio a, por ejemplo, cualquier polinomio. En esta tabla están las fronteras para n²-1:

N       Valores de a y b

115   65 140

290   71 364

315   174 385

4651 4131 5075

 

Números poligonales y piramidales

Como los números poligonales y piramidales son polinomios, valdría para ellos todo lo explicado anteriormente. Por ejemplo, los hexagonales siguen el polinomio H(n)=n(2n-1), por lo que se puede intentar buscar fronteras para ellos y sus sumas equivalentes.

Lo hemos intentado con las técnicas de frontera2, obteniendo estas soluciones:

N                 Valores de a y b

37               8 46

154             85 188

239             54 300

399             134 499

1288           574 1598

1779           469 2234

2099           59 2644

Comprobamos el último:

SUMAFUN(59;2098;"X*(2*X-1)")=6158445500

SUMAFUN(2100;2644;"X*(2*X-1)")=6158445500

 

Sumas de tetraedros

Y para finalizar, 44 es frontera para números tetraédricos, o piramidales triangulares, pues

SUMAFUN(10;43;"X*(X+1)*(X+2)/6")=162690

SUMAFUN(45;52;"X*(X+1)*(X+2)/6")=162690

La fórmula de los tetraedros la tienes en

https://es.wikipedia.org/wiki/N%C3%BAmero_tetra%C3%A9drico

También puedes consultar nuestra publicación

http://www.hojamat.es/publicaciones/piramidal.pdf

Frontera entre dos sumas equivalentes (1)

Descubrí en http://oeis.org/A094552 que 18921 separa dos sumas de cuadrados con idéntico total, una hasta él y otra a partir de él, sin incluirlo (también podría contarse con él). Después de investigarlo, llegué a esta  comprobación:

suma(i=10472,18920,i^2)=1875012353984

suma(i=18922,23145,i^2)=1875012353984

Aquí, más que la sucesión resultante con los números que cumplen esta condición, que ya está publicada en la dirección referida, nos interesarán los algoritmos que se puedan usar en este caso y en otros afines. Los primeros números publicados son:

52, 100, 137, 513, 565, 1247, 8195, 13041, 18921, 35344, 40223, 65918, 68906, 121759, 132720, 213831, 215221, 235469, 265654, 506049, 520654, 585046, 598337, 817454, 993142, 1339560, 1579353, 2331619, 2843086, 3594812…

Nuestro objetivo será, además, encontrar las dos sumas con igual total a las que el número separa. Para ello habrá que identificar previamente (y ese será el objetivo prioritario) los límites de esas dos sumas a partir de su inicio en n-1 y n+1 respectivamente. El problema será la lentitud del proceso, pues requiere dos bucles anidados para crear las sumas, y eso, en números de más de tres cifras, puede ser resultar poco eficiente en equipos pequeños. Por ello, plantearemos tres algoritmos, el primero el “ingenuo”, el que inicialmente nos viene a la mente, el segundo con el uso de técnicas algebraicas, y el tercero con acumulación progresiva de cada suma.

Primer algoritmo (ingenuo)

Hemos creado la función frontera0, para que, dado un número cualquiera, determine si cumple la propiedad o no y cuáles son los extremos de las dos sumas con igual total. Devolverá un “NO” o bien esos extremos.

La idea es ir sumando cuadrados a la derecha del número N. Terminaremos la búsqueda al llegar a 2N, porque la otra suma sólo podrá tener N sumandos (si no, invadiría el cero y los negativos) y la suma superior tendrá menos sumandos que la inferior (porque estos son mayores).

Una vez determinada una suma provisional, recorreremos el rango 1…N-1 en orden inverso (lo esperable es que no llegue al 1) y para cada suma inferior compararemos con la superior para ver si son iguales, en cuyo caso sí hay solución. Si no, seguimos añadiendo sumandos a ambas.

Listado de la función para Excel y Calc

Function frontera0(n)

Dim j, k, s, t, s1, p, q

Dim b$

 

t = 0 ‘Indicador de que hay solución. En principio t=0 porque no la hay.

s = 0 ‘Suma superior

j = n + 1 ‘Comienza en N+1

While t = 0 And j < 2 * n ‘No llega a 2N

s = s + j ^ 2 ‘Se suman los cuadrados

k = 1 ‘Se inicia la búsqueda de la suma inferior

s1 = 0 ‘Contiene la suma inferior

While t = 0 And k < n

s1 = s1 + (n - k) ^ 2 ‘Acumula la suma inferior en orden inverso

If s1 = s Then ‘Si ambas sumas son iguales, hay solución

t = 1 ‘Indicador de solución

p = n - k: q = j ‘Se recogen las soluciones

End If

k = k + 1

Wend

j = j + 1

Wend

If t = 0 Then frontera0 = "NO" Else frontera0 = Str$(p) + Str$(q) ‘Devuelve “NO” o la solución

End Function

Si planteamos una búsqueda sistemática con esta función, obtenemos las primeras soluciones, que coinciden con las publicadas en OEIS, pero con el añadido de los límites de las sumas:

N       Límites

52      7 65

100   55 122

137   22 172

513   169 642

565   330 687

1247 572 1545

Para probar que los límites son correctos se puede usar cualquier calculadora avanzada. Hemos usado Wiris, que es gratuita y muy clara en su aspecto. La probamos con la solución correspondiente al 137. Calculamos la suma de cuadrados desde 22 hasta 136 y, por otra parte, desde 138 hasta 172. Nótese que la suma superior tendrá siempre menos sumandos que la inferior.

De esta forma hemos comprobado que 137 es un término de la sucesión buscada.

Segundo algoritmo, con ayuda del Álgebra

Nos basamos en la fórmula de los primeros cuadrados desde 1 hasta n:

Si se conoce la suma de cuadrados s0 desde 1 hasta n-1 (de fórmula (n-1)*n*(2n-1)/6) y el valor de la suma superior s, restando s0-s equivaldrá a un k(k+1)(2*k+1)/6 para cierto valor de k. La ventaja es que ese valor se puede encontrar. Veamos cómo.

Si llamamos M a la diferencia s0-s, tendremos:

Esto nos da una cota superior para el valor de k

De igual forma:

Es sencillo comprenderlo al comparar las dos fracciones. Seguimos:

Por tanto, para cada suma superior podemos calcular la k correspondiente en la suma inferior (esa k se corresponde con la suma desde 1 hasta el tope inferior), quedándonos con la parte entera de esa raíz.

Este razonamiento evita el doble bucle, porque, para cada suma superior obtendremos el límite correspondiente en la inferior. El algoritmo quedaría según el listado de la segunda función de Excel, frontera1:

Function frontera1$(n)

Dim j, k, s, t, s1, s0, m, p, q

t = 0 ‘Indicador de solución

s = 0 ‘Suma superior

j = n + 1 ’Primer sumando

s0 = n * (n - 1) * (2 * n - 1) / 6 ‘Suma en n-1

While t = 0 And s < s0

s = s + j ^ 2

m = s0 – s ‘Diferencia entre sumas, para calcular k

k = Int((3 * m) ^ (1 / 3) + 0.000001) ‘Redondeamos por defecto

s1 = s0 - k * (k + 1) * (2 * k + 1) / 6 ‘Suma inferior calculada

If s1 = s Then t = 1: p = k + 1: q = j ‘Hay solución

j = j + 1

Wend

If t = 0 Then frontera1 = "NO" Else frontera1 = Str$(p) + Str$(q)

End Function

 

Tercer algoritmo (paso a paso se marcha mejor)

En el tercer intento comenzaremos con los valores s=(n+1)^2 y s1=(n-1)^2. Es evidente que s1<s, por lo que podemos ir añadiéndole sumandos hacia atrás a s1 hasta que sobrepase a s, Si llegado a este punto las sumas son iguales, hemos terminado y, si no, aumentamos alternativamente s y s1 hasta que se igualen o s1 llegue hasta el tope 0, con lo que no existirá solución.

Esta sería la función para el algoritmo tercero:

Function frontera2$(n)

Dim j, k, t, s1, s0, m, p, q

 

t = 0 ‘Indicador de solución

k = n – 1 ‘Índices de las sumas

j = n + 1

s0 = k ^ 2 ‘Inicios de las sumas

s1 = j ^ 2

While t = 0 And k > 0 ‘Bucle de seguridad por si no hay solución

While s0 < s1 And k > 0 And t = 0

k = k - 1

s0 = s0 + k ^ 2 ‘Se incrementa s0 si es menor que s1

Wend

 

While s0 > s1 And t = 0

j = j + 1

s1 = s1 + j ^ 22 ‘Se incrementa s1 si es menor que s0

Wend

If s1 = s0 Then t = 1: p = k: q = j ‘Si se igualan, hay solución

Wend

If t = 0 Then frontera2 = "NO" Else frontera2 = Str$(p) + Str$(q)

End Function

 

Este será quizás el algoritmo más rápido (no lo he cronometrado, pero se le ve con más velocidad). Es reconfortante comparar las tres posibilidades y comprobar la unicidad de resultados:

Como se afirmó en los primeros párrafos, el interés de este estudio residía en los algoritmos, y no en los resultados. En la siguiente entrada aplicaremos estas ideas a otros tipos de números.

Regresos 2: La mitad, cuadrado, el tercio, cubo

En los primeros tiempos de este blog se lanzaban retos a los lectores, pero luego se cambió el estilo. Entre ellos figuraba este:

Encuentra los primeros números naturales N que admiten estas dos descomposiciones:

N = 2n² = 3m³

(https://hojaynumeros.blogspot.com/2009/05/la-mitad-cuadrado-el-tercio-cubo.html)

 Búsqueda por razonamiento

La idea propuesta era jugar con los factores primos de cada miembro de la igualdad. Así, en m³ debe figurar el factor 2, y en n² el factor 3:

Los introducimos y nos quedarán dos potencias p² y q³:

2*3*3*p²=3*2*2*2*q³ o bien 18p²=24*q³

En el primer miembro falta el 2 respecto al segundo, que lo extraemos de p², y en el segundo falta un 3, extraíble de q³:

2*3*3*2*2*r²=3*2*2*2*3*3*3*s³, es decir,  72*r²=648*s³

Como 648/72=9, lo extraemos de r²:

72*3*3*u²=648*v³

Podemos hacer u=v=1 y resulta la primera solución: N=648

Así que 648 = 2*18² = 3*6³

Si  multiplicamos 648 por m⁶ , siendo m cualquier número natural, resultarán las demás, ya que m⁶ contendrá un cuadrado por un lado y un cubo por otro:

Esas soluciones están publicadas en http://oeis.org/A185270

0, 648, 41472, 472392, 2654208, 10125000, 30233088, 76236552, 169869312, 344373768, 648000000, 1147971528, 1934917632, 3127772232, 4879139328, 7381125000, 10871635968, 15641144712, 22039921152, 30485730888, 41472000000, 55576446408, 73470177792, 95927256072 (En OEIS siempre se inicia en 0 si es posible)

Ya que conocemos el procedimiento, crearemos una tabla de Excel:

En ella figuran las primeras sextas potencias, su producto por 648 y los valores para n y m en el enunciado del problema. Evidentemente, coinciden con los elementos publicados en OEIS.

De los razonamientos anteriores se desprende que el número mínimo (en este caso 648) ha de poseer solo los factores primos 2 y 3, y si después se multiplica por potencias sextas, aparecerán otros factores.

En la igualdad N = 2n² = 3m³ podemos llamar u al exponente del 2 en n y v al que tiene en m. Se cumplirá:

1+2u=3v, es decir, que u=(3v-1)/2

Esto obliga a que v sea impar, y dando valores:

Si v=1, u=1, N presentará un exponente igual a 3, que es el que tiene la solución 648.

Con el factor 3 podemos razonar igual, si r es su exponente en n y s el de m, se cumplirá: 2r=1+3s y r=(1+3s)/2, con lo que s también será impar.

Si s=1, r=2, y N tendrá de exponente 2r=4 (o 1+3s=4), que también coincide con el exponente de 648.

Ese tipo de razonamiento sería válido para otras propuestas.

 

Búsquedas con una función

En la entrada de hace años se proponía que N= 2n² = 5m⁵

La primera solución era el número  500000=2*500²=5*10⁵

Después habría que multiplicar por potencias décimas.

¿Y en el caso de N= 3n³ = 5m⁵ y otros similares?

Podemos caracterizar los números buscados mediante una función de hoja de cálculo. Está diseñada para tratar el caso general: N=p*n^p=q*m^q.

Public Function expocoef(n, p, q) As Boolean

‘Los parámetros son N y los dos exponentes p y q

Dim k, j

k = Int((n / p) ^ (1 / p) + 0.00000001) ‘Posible valor de n

j = Int((n / q) ^ (1 / q) + 0.00000001) ‘Posible valor de m

If p * k ^ p = n And q * j ^ q = n Then expocoef = True Else expocoef = False

End Function

Lo aplicamos al caso p=2 y q=3, los propuestos en un principio, buscamos los números que lo cumplen y queda:

No seguimos la búsqueda porque ya conocemos la teoría. Sólo se trataba de confirmarla.

En el caso de p=2 y q=5 podemos traducir la función a PARI, que es más rápido:

expocoef(n,p,q)={my(k,j);k=round((n/p)^(1/p));j=round((n/q)^(1/q));p*k^p==n&&q*j^q==n}

for(i=1,100000,if(expocoef(i,2,3),print(i)))

Es más sintético porque devuelve el valor p*k^p==n&&q*j^q==n, que da forma a la condición propuesta. Para p=2 y q=3 da rápidamente las dos primeras soluciones 648 y 41472:

Para p=2 y q=5 devuelve:

Ya conocíamos el valor 500000 como primera solución.

Otro ejemplo: para p=2 y q=7 la solución es:

N=737894528=2*19208^2=7*14^7

Aquí copiamos las primeras soluciones en los casos más simples:

 

Versión rápida de la búsqueda

Si solo estudiamos las primeras soluciones, sin factores extraños a los dados en la cuestión, podemos usar un código similar a este:

expocoef(n,p,q)={my(k,j);k=round((n/p)^(1/p));j=round((n/q)^(1/q));p*k^p==n&&q*j^q==n}

for(i=1,10,for(j=1,10,m=3^i*5^j;if(expocoef(m,3,5)>0,print(m))))

Está adaptado al caso de N= 3n³ = 5m⁵

Al usar solo potencias, es muy rápido, y nos da en segundos la primera solución:

Así podríamos proceder en otros casos.

 

Los pseudoprimos

Definición de pseudoprimo 

La idea de número pseudoprimo surge de los grandes teoremas de la Aritmética Modular

(Ver mi publicación http://www.hojamat.es/sindecimales/congruencias/teoria/teorcong.pdf):

Podemos comenzar por el de Euler: Si llamamos j(m) a la indicatriz de Euler de m, se cumplirá que

 a^j(m) =1 (mod m)

para todo a primo con m. (Teorema de Euler)

Si m es primo, la igualdad anterior se puede expresar como

a^m-1 =1 (mod m)

 (Pequeño Teorema de Fermat)

El recíproco no es cierto. Si para un a primo con m se cumple

a^m-1=1 (mod m), entonces m no tiene que ser necesariamente primo. A estos números compuestos que cumplen el teorema les llamaremos pseudoprimos de Fermat (hay otras clases de pseudoprimos). Este carácter dependerá del valor de la base a.

 

Identificación de pseudoprimos

No es nada complicado identificar un pseudoprimo respecto a una base dada. Las operaciones son sencillas, pero pueden alcanzar números muy grandes, por lo que tendremos que usar técnicas de Aritmética Modular en algunos casos, para abreviar cálculos y datos.

La primera operación es la de obtener el resto de una potencia respecto a un módulo, lo que llamamos resto potencial. En nuestra web figura una hoja de cálculo de hace años, muy simple, que los calcula para datos no muy grandes

http://www.hojamat.es/sindecimales/congruencias/herramientas/hoja/potenciales.xls

La teoría sobre restos potenciales también la puedes consultar en nuestro documento

http://www.hojamat.es/sindecimales/congruencias/teoria/teorcong.pdf

Aquí partiremos de una función que actuará sobre tres datos:

• ·       Base de la potencia b
• ·       Exponente p
• ·       Módulo m

Sobre ellos actuará la función RESTOPOT para Excel y LibreOffice Calc, que irá construyendo la potencia mediante multiplicaciones, pero convirtiendo cada resultado en resto módulo m, con lo que no se disparará la magnitud de los datos. Este es su listado:

Función RESTOPOT

Public Function restopot(b, p, n)

Dim r, m, i

 

r = b Mod n ‘Resto de la base respecto a m

m = 1

For i = 1 To p ‘Se construye la potencia con restos

m = m * r Mod n ‘m irá recorriendo los restos potenciales

Next i

restopot = m

End Function

 Por ejemplo, el resto de 3^26 respecto al módulo 7 sería RESTOPOT(3;26;7)=2, como puedes comprobar en la hoja potenciales.xls presentada más arriba:

 

Con esta función podemos averiguar si a^m-1 =1 (mod m)  y si m es compuesto, con lo que tendría el carácter de pseudoprimo.

Contando con la función RESTOPOT es fácil exigir que se cumplan las condiciones para ser pseudoprimo en una base dada.

 

Public Function espseudo(m, b) As Boolean

If Not esprimo(m) And mcd(m, b) = 1 And restopot(b, m - 1, m) = 1 Then espseudo = True Else espseudo = False

End Function

Nos limitamos a exigir que

• ·       Sea compuesto
• ·       Primo con la base
• ·       El resto potencial b^m-1 respecto a m sea 1

Con esta función y un bucle de búsqueda podemos reproducir muchas sucesiones de pseudoprimos ya publicadas en OEIS. Por ejemplo, para b=23 obtenemos esta lista:

Pseudoprimos en base 23

22, 33, 91, 154, 165, 169, 265, 341, 385, 451, 481,…

La puedes comprobar en http://oeis.org/A020151

En base 11

Obtenemos: 10, 15, 70, 133, 190, 259, 305, 481, 645, 703, 793, 1105, 1330, 1729, 2047, 2257

(Ver http://oeis.org/A020139)

 

Versión en PARI

Si deseas estudiar números mayores contando con la mayor velocidad de proceso de PARI, puedes usar este código debidamente adaptado a tus datos (está construido para base 23 y búsqueda hasta el 4000):

rpm(b,p,n)={my(r,m,i);r=b%n;m=1;for(i=1,p,m=(m*r)%n);m}

espseudo(m,b)=!isprime(m)&&gcd(m,b)==1&&rpm(b,m-1,m)==1

for(k=2,4000,if(espseudo(k,23),print1(k,", ")))

Lo hemos adaptado a base 17 y cota 20000, obteniendo:

4, 8, 9, 16, 45, 91, 145, 261, 781, 1111, 1228, 1305, 1729, 1885, 2149, 2821, 3991, 4005, 4033, 4187, 4912, 5365, 5662, 5833, 6601, 6697, 7171, 8481, 8911, 10585, 11476, 12403, 12673, 13333, 13833, 15805, 15841, 16705, 19345, 19729,…

Coinciden con los pseudoprimos publicados en http://oeis.org/A020145

 

Números de Carmichael

Si un número es pseudoprimo con base todos los números coprimos con él, se llama “de Carmichel”.

Los primeros los tienes en https://oeis.org/A002997:

561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, 29341, 41041, 46657, 52633,…

Bastará recorrer los números coprimos con uno de ellos y comprobar que es pseudoprimo con todos ellos.

Hay criterios más sencillos, que puedes consultar en

https://en.wikipedia.org/wiki/Carmichael_number.

 

Números de Sarrus o Poulet

Estos son los pseudoprimos en base 2, también llamados números de Sarrus, Poulet o simplemente psudoprimos, sin especificar el módulo.

El primer pseudoprimo módulo 2 es el 341, porque es compuesto (341=11*31) y cumple que

2³⁴⁰ =1 (mod 341)

Esta condición se verifica fácilmente, ya que 2¹⁰=1024=3*341+1 presenta resto 1 respecto al módulo 341, por lo que todas sus potencias, entre ellas 2³⁴⁰ también tendrán ese mismo resto.

El segundo pseudoprimo módulo 2 es 561, que es compuesto (561=3*11*17) y se verifica que

2⁵⁶⁰ =1 (mod 561)

La sucesión de números de Poulet la tienes en http://oeis.org/A001567

341, 561, 645, 1105, 1387, 1729, 1905, 2047, 2465, 2701, 2821, 3277, 4033, 4369, 4371, 4681, 5461, 6601, 7957, 8321, 8481, 8911, 10261, 10585, 11305, 12801, 13741, 13747, 13981, 14491, 15709, 15841, 16705, 18705, 18721, 19951, 23001, 23377, 25761, 29341...

Aquí nos hemos limitado a presentar conceptos básicos y facilitar la búsqueda de pseudoprimos. Se podría extender más su estudio, pero superaría los objetivos de este blog.

 

Números de Hogben

La elección de temas que efectúo para este blog tiene a veces carácter azaroso. Dentro de mis publicaciones en Twitter (@connumeros) descubrí que el número 1723 equivale a la suma de dos números triangulares de órdenes 40 y 42 respectivamente. Me gustó la idea y emprendí un estudio algebraico del tema:

Sean los órdenes k y k+2, con N como suma de dos triangulares. Tendremos:

 k(k+1)/2+(k+2)(k+3)/2=N

k(k+1)+(k+2)(k+3)=2N

K²+k+k²+5k=2N-6

2k²+6k=2N-6

4k²+12k=4N-12

(2k+3)²=4N-3

Esta identidad me llevó a buscar los números N en los que 4N-3 es un cuadrado, para después, posteriormente despejar el valor de k.

Emprendí la búsqueda y obtuve este listado:

Cuando obtengo un resultado así (podía haber comenzado con los valores de k), suelo buscarlo en la página OEIS (http://oeis.org/) y así fue como llegue a los números de Hogben (http://oeis.org/A002061), que no había tratado en este blog. Decidí cambiar mis planteamientos iniciales para dedicarme a estudiar esos números con mis herramientas usuales. Como dan lugar a muchas curiosidades, y están todas muy bien desarrolladas en distintas páginas, iré enlazándolas cuando crea que no puedo aportar nada nuevo.

Números de Hogben

Podemos definirlos como aquellos que son suma de dos número triangulares cuyos órdenes se diferencian en dos unidades, pero también vemos en la tabla que H(k)=k²-k+1, como por ejemplo H(5)=25-5+1=21, y H(7)=49-7+1=43.

Si despejo N en una igualdad anterior, me queda:

(2k+3)²=4N-3; 4N=4k²+12k+9+3; N=k²+3k+3

Puedo expresar N en función de k+2:

N=k²+3k+3=(k+2)²-(k+2)+1

Para que coincida esta expresión con la generación de la tabla basta elegir k como el índice mayor de los dos triangulares que se suman, es decir, k+2, y así se establece la coincidencia de métodos.

N= k²-k+1

Esta es la definición que se usa en http://oeis.org/A002061. Hay que recordar que en OEIS se prefiere iniciar las sucesiones con índice 0:

A002061                            Central polygonal numbers: a(n) = n^2 - n + 1.

1, 1, 3, 7, 13, 21, 31, 43, 57, 73, 91, 111, 133, 157, 183, 211, 241, 273, 307, 343, 381, 421, 463, 507, 553, 601, 651, 703, 757, 813, 871, 931, 993, 1057, 1123, 1191, 1261, 1333, 1407, 1483, 1561, 1641, 1723, 1807, 1893, 1981, 2071, 2163, 2257, 2353, 2451, 2551, 2653

Estos números, rotulados como “poligonales centrales” son los números de Hogben.

Si situamos los números naturales en espiral, los de Hogben ocupan los extremos de la diagonal principal, tal como podemos observar en la tabla creada con hoja de cálculo:

La razón estriba en que la diferencia entre dos números de Hogben consecutivos es

H(n+1)-H(n)=(n+1)²-n-1+1-n²+n-1=2n

Vimos más arriba que H(5)=21, luego su diferencia con el siguiente será 2*5=10, y en la espiral vemos que se necesitan diez pasos para ir de 21 a 31. Como el número de pasos va creciendo de 2 en 2 y el incremento H(n+1)-H(n) también, se dará esa coincidencia en todos los casos.

La anterior fórmula se puede interpretar como una recursión:

H(n+1)=H(n)+2n

Por ejemplo, 13 es el número de Hogben de índice 4, luego el siguiente será 13+2*4=21, como era de esperar.

Con nuestra herramienta para prolongar recurrencias podemos buscar una de tipo homogéneo, y, en efecto, es muy simple:

H(n+3)=3*H(n+2)-3*H(n+1)+H(n)

(http://www.hojamat.es/blog/ecurrecurre.xlsm)

Es así por ser un polinomio de segundo grado, y con ellos funciona esta recurrencia siempre. Lo puedes comprobar con esta captura de pantalla de la calculadora Wiris (https://calcme.com/a)

Se ha desarrollado la suma de la recurrencia y el resultado esperado, obteniendo el mismo resultado.

Dados tres términos consecutivos, como 31, 43, 57, se cumple que el siguiente, 73, se puede encontrar de la forma 3*57-3*43+31, y así es, porque el resultado es 73.

En la entrada de blog http://voodooguru23.blogspot.com/2018/11/hogben-numbers.html puedes consultar algunas propiedades interesantes de estos números. Están bien desarrolladas y sería inútil repetirlas aquí.

Una interpretación sencilla de estos números es que n²-n+1 equivale a n(n-1)+1, es decir, a un número oblongo (y por tanto rectangular) al que le añadimos una unidad. Lo hemos representado así:

En la siguiente página se intenta explicar por qué Sloane y Plouffe llamaron a estos números “poligonales centrales”. Es interesante su lectura.

http://mrob.com/pub/seq/a002061.html

 

Cuatro propiedades aritméticas

(1) Según afirma Amarnath Murthy en la página de OEIS enlazada, el número de Hogben H(n) se puede interpretar como el término n de una progresión de diferencia n que comienza en 1. En efecto:

N=1: D=1: H(n)=1

N=2, D=2: 1, 3

N=3, D=3: 1, 4, 7

N=4, D=4: 1, 5, 9, 13

Vemos que todas las progresiones así construidas finalizan en un número de Hogben.

Esto es ningún misterio. Según la teoría de las progresiones tendremos:

H(n)=H(1)+D*(n-1)=1+n(n-1)=n²-n+1, que es la fórmula de estos números.

(2) Los números de Hogben son los residuos de n³ respecto a n²+1

Con la función RESIDUO de Excel y Calc es fácil comprobarlo:

Algebraicamente también es fácil, porque n³=(n-1)*(n²+1)+n²-n+1 con lo que el residuo es

n²-n+1=H(n)

(3) Los números de Hogben H(n) se representan como 111 en la base (n-1)

Por ejemplo, 7(10 = 111(2,  13(10=111(3,  21(10=111(4

La razón es que H(n+1)=(n+1)²-(n+1)+1 por definición, y simplificando queda n2+n+1, lo que significa 111(n.

 

(4) Si recordamos el cociente entre una suma de potencias y la suma de sus bases, obtendremos un sencillo resultado:

Así que basta dividir el cubo de n³+1 entre n+1 para obtener H(n):

H(4)=(64+1)/(4+1)=13

H(7)=(343+1)/(7+1)=344/8=43