Pares de números primos con la misma diferencia de cuadrados

En mis cálculos diarios en Twitter (@connumeros) me encontré por casualidad con cuatro primos con diferencias de cuadrados iguales, tanto de consecutivos como si los tomamos de forma alterna. Eran estos:

23, 43, 163 y 167

Sus diferencias de cuadrados iguales son dos:

167^2-163^2=43^2-23^2

167^2-43^2=163^2-23^2

Esto es porque 23^2+167^2=28418=43^2+163^2

Es evidente que la tercera forma de crear diferencias (cuarto con primero y tercero con segundo) no nos devolvería una igualdad.

Es esta una situación que se presta a crear métodos o algoritmos para la búsqueda de nuevos conjuntos de cuatro primos. No tiene más trascendencia el tema, y si no te atraen estas técnicas, no te servirá de mucho esta entrada.

Uso de la hoja “Cartesius”

Lo primero que me planteé ante este ejemplo es la cuestión de si existirían muchos conjuntos similares del mismo tipo. No tenía ninguna opinión previa, por lo que acudí a mi hoja “Cartesius” para ver si había algo útil entre los primeros primos. Es una herramienta lenta, por lo que solo exploré hasta el número 61. Mi gran sorpresa fue que resultaron muchos ejemplos posibles para los primeros primos.

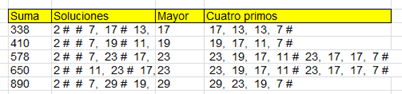
Este fue el resultado:

En las primeras columnas figuran los cuatro primos en orden creciente y en las siguientes los dos tipos de diferencias que resultan ser iguales. Todas son divisibles entre 4, por ser un producto de suma por diferencia entre impares.

Código

Lo que sigue es un poco específico, propio del lenguaje de “Cartesius”, pero creo que merece la pena explicarlo. Estas son las condiciones impuestas a “Cartesius”:

xtotal=4

xt=1..65

xt=filtro(primo)

es (x2^2-x1^2)=(x4^2-x3^2)

es (x1<x2)*((x2<x3)+(x2=x3))*(x3<x4)>0

Las tres primeras se entienden bien: combinaremos cuatro números (xtotal=4) desde 1 hasta 65 (xt=1..65) y exigiremos que sean primos (xt=filtro(primo)). Con estas condiciones se preparan automáticamente los primos que se van a combinar, según vemos en esta imagen:

En total, dieciocho primos, que combinaremos de todas las formas posibles (por eso la herramienta es lenta).

La tercera condición exige la igualdad entre diferencias de cuadrados:

es (x2^2-x1^2)=(x4^2-x3^2)

Exige que sean iguales las diferencias entre consecutivos, lo que garantiza que también sean iguales las diferencias alternadas. La palabra “es” significa que se exige que sea verdadera la expresión que le siga.

es (x1<x2)*((x2<x3)+(x2=x3))*(x3<x4)>0

Esta última condición elimina casos repetidos. Exige que X3 sea menor que X4, X1 menor que X2 y X2 menor o igual que X3.En “Cartesius”, como en otros lenguajes, el producto funciona como la conectiva lógica Y y la suma como la O.

Con este proceso ya tenía la idea de que estos casos abundarían en cualquier rango de números, y, por su naturaleza, que serían infinitos (conjetura). Se observan varios números en la cuarta columna que son cabecera de varios conjuntos, como el 61, que pertenece a varias soluciones.

Otra observación en la tabla es la de que están un poco mezclados los primos de tipo 4K+1 y con los de 4K+3.

Algoritmo en forma de función

Ya que este blog va de números y hoja de cálculo, parece conveniente acudir a esta herramienta general para completar y comprobar lo conseguido con Cartesius. La estructura de la función que presentaremos requiere el uso de cuatro bucles distintos, uno por cada primo al cuadrado, y en este caso serán del tipo WHILE_WEND, pero es fácil comprobar que no ralentizan mucho el proceso.

La función, tipo String o texto, actuará sobre un primo cualquiera (si no es primo, sale del código con la palabra “NO”) y devolverá todos los conjuntos de cuatro primos cuyo primer elementoo es ese número primo. Así se consigue una búsqueda sistemática si se desea.

Usaremos nuestra función PRIMANT, que devuelve el primo anterior a un número, porque la búsqueda de primos será descendente.

Este es el código de la función:

Function dos_dif_cubos(n)

Dim i, j, k, d, d1

Dim s$

If Not esprimo(n) Then dos_dif_cubos = "NO": Exit Function

s = ""

k = n

While k > 2 ‘Segundo primo, porque n es el primero

d = n ^ 2 - k ^ 2 ‘Primera diferencia de cuadrados

j = k

While j > 2 ‘Tercer primo

i = j

While i > 2 ‘Cuarto primo

d1 = j ^ 2 - i ^ 2 ‘Segunda diferencia

If d1 = d And d <> 0 And d1 <> 0 Then s = s + Str$(n) + ", " + Str$(k) + ", " + Str$(j) + ", " + Str$(i) + " # " ‘Se da la igualdad buscada

i = primant(i) ‘Desciende i

Wend

j = primant(j) ‘Desciende j

Wend

k = primant(k) ‘Desciende k

Wend

if s="" then s="NO"

dos_dif_cubos = s

End Function

Devuelve una cadena con todos los conjuntos de cuatro primos que presentan diferencias iguales dos a dos, y cuyo sumando mayor es n².

Por ejemplo, para el primo 23 obtendríamos:

23,  19,  17,  11 #  23,  17,  17,  7 #

Con ellos podríamos construir estas igualdades entre diferencias de cuadrados:

23^2-19^2=17^2-11^2

23^2-17^2=19^2-11^2

23^2-17^2=17^2-7^2

Con esta función podemos recorrer sistemáticamente cualquier rango de números primos (si alguno no es primo devolverá un “NO”).

Por ejemplo, esta sería la tabla de resultados para los primeros primos. Así que con esta función podemos crear un catálogo sistemático de los posibles conjuntos de cuatro primos con la propiedad buscada.

 

Estas cadenas de conjuntos de cuatro primos para uno dado se pueden conseguir también con Cartesius. Basta adaptar el código de más arriba a un valor concreto, por ejemplo el 61:

xtotal=3

xt=1..61

xt=filtro(primo)

es (x2^2-x1^2)=(61^2-x3^2)

es (x1<x2)*((x2<x3)+(x2=x3))*(x3<61)>0

 

Obtendremos una lista de cinco conjuntos de primos que se completan con el 61:

Esta solución coincide con la de la función dos_dif_cubos:

DOS_DIF_CUBOS(61)= 61,  59,  23,  17 #  61,  59,  19,  11 #  61,  59,  17,  7 #  61,  53,  31,  7 #  61,  47,  41,  13 #                                  

Con esto damos por resuelta la búsqueda. Nos queda un detalle, con el que comenzamos este estudio, y es la procedencia de estas diferencias de dos sumas de cubos con el mismo resultado.

Sumas de cubos equivalentes

Recordamos las frases de inicio de estas búsquedas:

23, 43, 163 y 167

Sus diferencias de cuadrados iguales son dos:

167^2-163^2=43^2-23^2

167^2-43^2=163^2-23^2

Esto es porque 23^2+167^2=28418=43^2+163^2

Si ahora buscáramos todos los números que equivalen al menos a dos sumas de cuadrados de primos, encontraríamos dos igualdades de diferencias del tipo buscado. Usaremos esta descomposición de un número en dos cuadrados de primos que sigue. Es una cadena de texto, y el primer carácter es el número de descomposiciones de ese tipo que presenta. Si no es posible la descomposición devolverá un “NO”.

Public Function sumadoscuad_prim$(n)

Dim i, r, t, w, m

Dim s$

s = "" ‘Variable de respuesta

m = 0 ‘Contador de soluciones

r = Sqr(n) ‘Tope de búsqueda

i = 2

While i < r

t = n - i ^ 2

w = Sqr(t)

If escuad(t) And esprimo(w) And i <= w Then m = m + 1: s = s + " # " + Str$(i) + ", " + Str$(w)

‘Si es cuadrado de un primo se incrementa m y se incorpora a la solución

i = primprox(i)

Wend

If s = "" Then s = "NO" Else s = ajusta(m) + " # " + s

sumadoscuad_prim = s

End Function

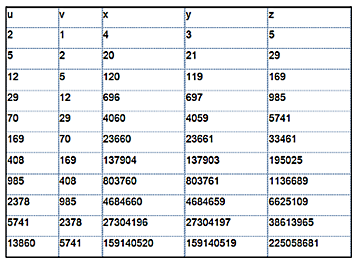
Con esta función se pueden unificar las dos cuestiones, enlazando diferencias y sumas, según vemos en la siguiente tabla, que elige el primo mayor y lo incorpora a una diferencia. Comprende todos los números enteros que equivalen a dos sumas de cuadrados de primos:

 

Tomamos el primo mayor y creamos con él diferencias de cuadrados, que coinciden con los elementos de la izquierda.

 

Regresos 6 – Oblongos y pitagóricos (2)

 En esta entrada seguimos trabajando con los valores de N tales que N y N+1 son catetos en una terna pitagórica y abrimos otras posibilidades.

Relación con triangulares

Área triangular y oblonga

Ya se comentó en la anterior entrada que el área del triángulo rectángulo de catetos N y N+1 es un número triangular. En la sucesión que nos ocupa, las áreas son las siguientes (prescindimos del cero):

6, 210, 7140, 242556, 8239770, 279909630, 9508687656, 323015470680, 10973017315470,…

Están contenidas en http://oeis.org/A029549

En mi entrada  de blog

 http://hojaynumeros.blogspot.com/2021/05/triangulares-que-son-oblongos.html)

Se llega a la misma sucesión si exigimos que unos números sean triangulares y oblongos a la vez

En la parte inferior de la imagen se puede leer el código PARI usado.

Estas áreas están publicadas en http://oeis.org/A029549

A029549    a(n + 3) = 35*a(n + 2) - 35*a(n + 1) + a(n), with a(0) = 0, a(1) = 6, a(2) = 210.   

0, 6, 210, 7140, 242556, 8239770, 279909630, 9508687656, 323015470680, 10973017315470, 372759573255306, 12662852473364940, 430164224521152660, 14612920781245825506, 496409142337836914550, 16863297918705209269200

Resumimos la situación en la siguiente tabla, en la que en la última columna figuran las expresiones del área como número oblongo.

Por tanto, las hipotenusas de estas ternas son números triangulares y también oblongos, es decir, son el doble de otro triangular.

Otras diferencias entre catetos

Si tomamos la terna 3, 4, 5 y multiplicamos sus lados por un mismo número, es evidente que resultará otra terna, pero no primitiva, en la que los catetos se diferenciarán en el factor de multiplicación que hayamos usado.

Así que cualquier número entero puede ser diferencia entre catetos. Además, si es diferencia en una terna, puede serlo en infinitas. La causa es que si en la generación de terna mediante los valores (u²-v², 2uv, u²+v²), también tendrán la misma diferencia si sustituimos u, v por 2u+v, u. En efecto, los lados serían:

Hipotenusa: (2u+v)²+u²=4u²+v²+4uv+u²=5u²+v²+4uv

Cateto 1: (2u+v)²-u²=4u²+v²+4uv-u²=3u²+v²+4uv

Cateto 2: 2*(2u+v)*u=4u²+2uv

Diferencia u²-v²-2uv

Es la misma diferencia que entre los dos catetos primitivos, u²-v² y 2uv

Lo vemos con un ejemplo: Si u=2 y v=1, resulta la conocida 3, 4 y 5, con diferencia 1 entre catetos. Si aplicamos la transformación 2u+v, u, queda que u=2*2+1=5 v=2, Cateto 1: 5²-2²=21, 2*5*2=20, y mantienen la misma diferencia 1.

Reiterando el procedimiento obtendremos infinitas ternas con la misma diferencia (salvo signo u orden). Si la primera es primitiva, todas las demás lo serán, porque si u y v son primos entre sí, también lo serán 2u+v y u.

Ejemplo:

De los valores u=4, v=3, x=7, y=24, z=25, con diferencia entre catetos igual a 17, podemos engendrar u=11, v=4, x=88, y=105, z=137, con 105-88 = 17 y después u=26, v=11, x=572, y=555 z=797, y así tantas como queramos.

Valores de las diferencias

Si sólo admitimos ternas primitivas, no todos los números pueden ser diferencia de catetos. Los únicos posibles son 1, 7, 17, 23, 31, 41, 47, 49, 71, 73, 79, 89, 97, 103, 113, 119, ...

La razón es que las diferencias han de tener factores primos del tipo 8k+1 o bien 8k-1 (Ver http://oeis.org/A058529)

Otras relaciones entre hipotenusa y cateto

En las últimas cifras

Existen muchas hipotenusas que coinciden con catetos en las dos últimas cifras. Para que el estudio no tenga casos triviales, eliminamos los que terminan en dos ceros. Un ejemplo sería la terna (260, 288, 388), en la que dos lados terminan en 88. No es difícil encontrar hipotenusas de este tipo. Podemos probar esta función para Excel, en la que n es el número a estudiar y c el número de cifras en las que coincide con un cateto:

Function hip_mod_cat(n, c)

Dim i, m, p, r

Dim s$

s = "" ‘En esta cadena se volvará la terna pitagórica

m = 10 ^ c ‘Esta variable contendrá 10^c, 10, 100, 1000…

r = n Mod m ‘Encuentra las últimas cifras

If r = 0 Then hip_mod_cat = "NO":  Exit Function ‘Desechamos potencias de 10

For i = r To n - m Step m

'If n - i Mod m = 0 Then ‘Tienen cifras iguales

If escuad(n ^ 2 - i ^ 2) Then p = Sqr(n ^ 2 - i ^ 2): s = s + Str$(p) + ", " + Str$(i) + ", " + Str$(n) ‘Si es un cateto, creamos la terna en modo texto

'End If

Next i

If s = "" Then s = "NO"

hip_mod_cat = s

End Function

Con esta función se puede crear un bucle de búsqueda y obtenemos estas ternas:

Observamos que algunas hipotenusas presentan dos soluciones. Podíamos estudiar este caso, pero no merece la pena, para una simple curiosidad.

Como el proceso de búsqueda es rápido y aparecen pronto muchas soluciones, no abandonaremos la hoja de cálculo para buscar otros instrumentos.

El tercer cateto será siempre múltiplo de 10, ya que es la raíz cuadrada de una diferencia de cuadrados con las cifras últimas coincidentes.

Como curiosidad, estas son las soluciones para tres cifras, por si deseas reproducirlas. El comportamiento del otro cateto te dará una pista para entender el proceso.

Así que es condición necesaria que el tercer cateto termine en ceros.

 

Hipotenusa y cateto anagramáticos

Finalizamos esta exploración con un ejemplo más de relación entre hipotenusa y cateto. Con él y todo lo anterior como base, se pueden intentar otras búsquedas, que ya no entran aquí. Lo dejamos como propuesta.

Dos números son anagramáticos si poseen las mismas cifras y con la misma frecuencia. Para estudiarlos usaremos nuestra función digiordenado, que ordena las cifras de un número entero. La puedes consultar en esta entrada del blog:

https://hojaynumeros.blogspot.com/2017/05/sumas-anagramaticas.html

Con esta función es fácil saber si dos números son anagramáticos, pues entonces digiordenado dará el mismo resultado en ambos. Con esta idea, hemos construido una dunción similar a las anteriores. Es esta:

Function hip_anam_cat(n)

Dim i, p, r

Dim s$

s = ""

For i = 1 To n - 1

If digiordenado(n) = digiordenado(i) And escuad(n ^ 2 - i ^ 2) Then

p = Sqr(n ^ 2 - i ^ 2): s = s + Str$(p) + ", " + Str$(i) + ", " + Str$(n)

End If

Next i

If s = "" Then s = "NO"

hip_anam_cat = s

End Function

No necesita explicación. Con ella hemos encontrado estos ejemplos:

La tercera columna es la de hipotenusas, que son anagramáticas con el segundo cateto. Se observan soluciones dobles en 650 y 765.

El primer cateto siempre será múltiplo de 3, pues si los otros dos lados tienen las mismas cifras, la diferencia de sus cuadrados será múltiplo de 9 y, por tanto, su cuadrado lo será, luego el cateto será múltiplo de 3.

Como curiosidad, esta sería la versión para el lenguaje PARI:

is(n)={my(k=1,v=0);while(k<=n-1&&v==0,if(issquare(n*n-k*k)&&vecsort(digits(k))==vecsort(digits(n)),v=1);k+=1);v}

for(i=1,10000,if(is(i),print1(i,", ")))

Aquí, digiordenado se sustituye por vecsort(digits(k))

Devuelve las hipotenusas:

65, 153, 180, 218, 325, 327, 351, 436, 545, 615, 629, 650, 654, 702, 740, 763, 765, 807, 872, 925, 975, 981, 1325, 1453, 1480, 1530, 1625, 1635, 1640, 1800, 1865, 1872, 1940, 2132, 2180, 2601, 2725…

Con estos ejemplos ya podemos emprender otras búsquedas similares.

 

Regresos 6 – Oblongos y pitagóricos (1)

 Desde la publicación de nuestra entrada de título “Oblongos y pitagóricos” (https://hojaynumeros.blogspot.com/2010/03/oblongos-y-pitagoricos-3.html) hemos estudiado algunas relaciones entre catetos e hipotenusa dentro de una terna pitagórica. Parece conveniente repasar las mismas, eliminando lo accesorio, y efectuar una síntesis de varias entradas.

Catetos que se diferencian en una unidad

Comenzaremos con un repaso a la primera cuestión que publicamos:

Una cuestión que ha dado juego desde los tiempos de Girard y Fermat y que permite recorrer alternativas de cálculo es la siguiente:

De todos los triángulos rectángulos de lados enteros ¿Cuáles cumplen que la diferencia entre los catetos es la unidad?

Recordábamos que la primera terna en cumplir esta condición es la popular 3, 4 y 5. El resto resultará de la ecuación x²+(x+1)²=y².

Otra forma de expresarlo es que el área del rectángulo formado por los dos catetos es un número oblongo, tipo N(N+1) y, por tanto, el área del triángulo será triangular (N(N+1)/2).

Podemos resolverla mediante búsqueda y con técnicas algebraicas.

Búsqueda

Como últimamente usamos funciones, organizaremos la búsqueda con la siguiente:

Function catetoscons$(n)

Dim a

Dim s$

s = ""

a = n^2 + (n+1)^2

If escuad(a) Then s = Str$(n) + Str$(n + 1) + Str$(Sqr(a))

catetoscons = s

End Function

 

Su funcionamiento se entiende bien: si n^2+(n+1)^2 es cuadrado, devuelve la terna completa. Las primeras conseguidas son:

Los valores de N están publicados en http://oeis.org/A001652. Volveremos a esta sucesión para revisar algunas propiedades.

Versión en PARI

Con este código avanzaremos más lejos en los valores de N:

is(n)={issquare(n^2+(n+1)^2)}

for(i=1,10^9,if(is(i),print1(i,", ")))

Obtenemos este resultado:

3, 20, 119, 696, 4059, 23660, 137903, 803760, 4684659, 27304196, 159140519,

Hemos llegado más lejos, pero con tantas cifras la búsqueda se hace muy lenta. Es preferible algún otro procedimiento más rápido, por lo que pasamos al Álgebra:

Estudio algebraico

La ecuación x²+(x+1)²=y² se puede desarrollar de esta forma: x²+(x+1)²=y²;  2x²+2x+1=y²; (2x+1)²+1=2y²; (2x+1)² - 2y² = -1, por lo que llamando z=2x+1 desembocamos en una ecuación de Pell con segundo miembro igual a -1

Z²-2y² = -1

Utilizamos la hoja de cálculo pell.ods o pell.xlsm contenidas en la dirección

http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm

con el resultado que indica la imagen siguiente

en la que valdrán las soluciones correspondientes a -1

Z=1;   Y=1;       Imposible, pues X sería negativo

Z=7;   Y=5         X=3; X+1=4; Y=5

Z=41; Y=29      X=20; X+1=21; Y=29

Z=239; Y=169   X=119; X+1=120; Y=169

Z=1393; Y=985 X=696; X+1=697; Y=985

Este método tiene el inconveniente de que depende de la precisión que tenga la hoja de cálculo en los números con coma flotante, lo que hará que se rompa en algún momento la periodicidad de los cocientes, en este caso el 2. Por ello se puede completar con una fórmula recursiva que obtenga soluciones exactas conociendo las primeras.

En este ejemplo cada elemento de las distintas celdas cumple la fórmula

a_n+2 = 2a_n+1 + a_n

pero como las soluciones aparecen de forma alternada, deberemos reiterar dos veces, y nos quedará:

a_n+4 = 2a_n+3 + a_n+2 = 2(2a_n+2 + a_n+1)+ 2a_n+1 + a_n = 4a_n+2 + 4a_n+1+ a_n = 6a_n+2 -  a_n

Con esta fórmula recursiva se van obteniendo las soluciones sin errores a partir de las dos primeras:

Z₀ = 1; Z₂ = 7; Z₄ = 6*7-1 = 41; Z₆ = 6*41-7 =239;…

Y₀ = 1; Y₂ = 5; Y₄ = 6*5-1 = 29; Y₆ = 6*29-5 =169;…

Pero no olvidemos que Z es una variable auxiliar Z=2X+1 y que después debemos despejar X

La siguiente lista de ternas, que coincide con la primera que propuso Girard, se ha obtenido mediante esta técnica. Los valores de N coinciden con los de la segunda columna.

1	0	1
5	3	4
29	20	21
169	119	120
985	696	697
5741	4059	4060
33461	23660	23661
195025	137903	137904
1136689	803760	803761
6625109	4684659	4684660
38613965	27304196	27304197
225058681	159140519	159140520
1311738121	927538920	927538921
7645370045	5406093003	5406093004
44560482149	31509019100	31509019101
259717522849	183648021599	183648021600
1513744654945	1070379110496	1070379110497
8822750406821	6238626641379	6238626641380
51422757785981	36361380737780	36361380737781
299713796309065	211929657785303	211929657785304

Los valores de N coinciden con los contenidos en http://oeis.org/A001652, que, por cierto, usa esta recurrencia como definición, que con el cambio de variable entre Z y X queda así:

a(n) = 6*a(n-1) - a(n-2) + 2 with a(0) = 0, a(1) = 3.

0, 3, 20, 119, 696, 4059, 23660, 137903, 803760, 4684659, 27304196, 159140519, 927538920, 5406093003, 31509019100, 183648021599, 1070379110496, 6238626641379, 36361380737780, 211929657785303,

Con hoja de cálculo ya no podemos seguir, por el problema de la coma flotante. Lo podemos intentar con PARI:

a=0;b=3;print1(a,", ");print1(b,", ");while(a<10^20,c=6*b-a+2;print1(c,", ");a=b;b=c)

Como llegamos a 10^20, en pocos segundos se avanza en la lista de valores de N:

Una curiosidad

Cuando no se tienen claras las fórmulas de recurrencia lineal, pero se dispone de suficientes términos iniciales. Se puede acudir a mi hoja de cálculo ecurrecurre, disponible en la dirección

http://www.hojamat.es/blog/ecurrecurre.xlsm

En este caso usamos como datos los términos iniciales 0, 3, 20, 119, 696, y elegimos la variedad “No homogénea”, para que admita el sumando independiente 2. Pulsamos el botón de resolver y nos devuelve los coeficientes 6, -1 y 2.

Recurrencia doble

Fermat propuso una fórmula de recurrencia para generar ternas de este tipo a partir de otras similares. Dada la terna (x,x+1,y), se puede generar otra similar (x’,x’+1,y’) mediante las fórmulas x’=2x+3y+1  y y’=4x+3y+2.

Cuando se buscan las soluciones de la ecuación de Pell las recurrencias vienen dadas por las fórmulas de recurrencia z_n+1=z_n*z₀+D*y_n*y₀  y_n+1=z_n*y₀+y_n*z₀, pero en el caso z²-2y² = -1 las soluciones surgen de forma alternada.

Así, como en este caso z₀=1, y₀=1, tendremos:

z_n+1=z_n+2y_n; y_n+1=z_n+y_n  y reiterando dos veces

Z’’=Z’+2Y’=(Z+2Y)+2(Z+Y) = Z+2Y+2Z+2Y = 3Z+4Y

Y’’=Z’+Y’ = Z+2Y+Z+Y = 2Z+3Y

Teniendo en cuenta que Z=2X+1, y que Y=X+1, nos resulta

Y’’=2Z+3Y=2(2X+1)+3Y = 4X+3Y+2, que es la segunda fórmula de Fermat

De Z’’=3Z+4Y podemos obtener (2X’’+1)=3(2X+1)+4Y;  2X’’ = 6X+4Y+2;

X’’ = 3X+2Y+1, que es la primera

Aplicamos estas dos fórmulas al cateto menor y a la hipotenusa y obtenemos los mismos resultados a partir de 3, 4 y 5

X''=3X+2Y+1        X+1   Y''=4X+3Y+2

3        4        5

20      21      29

119   120   169

696   697   985

4059 4060 5741

23660 23661 33461

137903 137904   195025

803760 803761   1136689

4684659 4684660 6625109

27304196  27304197  38613965

159140519 159140520 225058681

 Uso de la generación de ternas

 La terna 3, 4, 5 está engendrada por las fórmulas clásicas 2uv, u²-v² y u²+v² para u=2 y v=1. Si sustituimos u y v por u, v+2u se mantendrá la misma diferencia entre catetos.

Basta ver que si engendramos los nuevos catetos y los restamos (en orden contrario) resultará: 2u(v+2u) - (v+2u)²+u²= 2uv+4u²-v²-4u²-4uv+u² = u²-v²-2uv, que es la diferencia original.

Esto nos permite engendrar de nuevo la lista que estamos considerando, tomando, n primer lugar u=2 v=1, y generando con ella la primera terna 3, 4 y 5. Después se aplica la fórmula de recurrencia  u_n = 2u_n-1+v_n-1 v_n = u_n-1 y se vuelve a generar una terna con ella, que resultará tener la misma diferencia pero con signo cambiado. Así hemos generado la lista con hoja de cálculo:

Con este cálculo abandonamos los algoritmos, y en la siguiente entrada pasaremos a propiedades curiosas de este tipo de ternas.