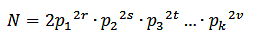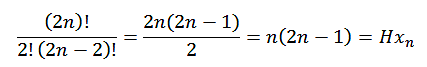Productos palindrómicos

En nuestras búsquedas de números y de desarrollos curiosos nos hemos encontrado a menudo con operaciones que dan lugar a números capicúas o palindrómicos (en esta entrada usaremos la palabra capicúa, que es más popular entre nosotros). Para abreviar, nos restringiremos a la operación producto con datos no necesariamente capicúas, pero cuyo resultado sí  lo es. Usaremos factores cercanos como objetivo de la búsqueda.

Siguiendo la costumbre general, consideramos capicúas a los de una cifra.

En este blog disponemos de la función ESCAPICUA, que puedes consultar en el Anexo de nuestra entrada https://hojaynumeros.blogspot.com/2020/02/suma-y-producto-de-cubo-y-otro-tipo-1.html El problema es que depende mucho de la estructura del lenguaje VBASIC DE Excel y Calc. Proponemos una nueva versión que se traslada mejor a otro lenguaje:

Function escapicua(n) As Boolean

Dim a, b, c, i, j, t

Dim es As Boolean

If n < 10 Then escapicua = True: Exit Function ‘Si es de una cifra, es capicúa

es = True ‘Suponemos que es capicúa

c = 1

While n >= 10 ^ c: c = c + 1: Wend ‘Calcula el número de cifras

t = Int((c + 1) / 2) ‘Punto medio de las cifras

i = 1

While i <= t And es

a = Int((n - Int(n / 10 ^ i) * 10 ^ i) / 10 ^ (i - 1)) ‘a y b son cifras simétricas

j = c - i + 1

b = Int((n - Int(n / 10 ^ j) * 10 ^ j) / 10 ^ (j - 1))

If a <> b Then es = False ‘Si las cifras simétricas son desiguales, no es capicúa

i = i + 1

Wend

escapicua = es

End Function

 

Con esta función es fácil analizar si un producto es capicúa o no. Podéis elegir la versión que más os guste.

En el lenguaje PARI, al poder usar listas y vectores, la función es muy simple. La que sigue se inspira en la propuesta por Michel Marcus:

ispalindromic(n) = my(d = digits(n)); Vecrev(d) == d

La función digits convierte el número en un vector de cifras y solo queda comprobar que es idéntico a su reverso.

 Productos entre números próximos

Caso N(N+1)

Un caso sencillo es el de multiplicar dos números consecutivos para dar como resultado un número oblongo (ver http://oeis.org/wiki/Oblong_numbers)

En hoja de cálculo basta construir una columna con productos N(N+1) y después aplicarle la función ESCAPICUA. Nosotros hemos usado un sencillo buscador que realiza la misma función, con este resultado:

Estos primeros casos están publicados en http://oeis.org/A028336

Con nuestra función en PARI podemos llegar más lejos sin esfuerzo:

Código:

ispalindromic(n) = my(d = digits(n)); Vecrev(d) == d

for(i=1,10^6,if(ispalindromic(i*(i+1)),print(i,"  ",i*(i+1))))

Es curioso el caso del 77, que siendo capicúa, produce un oblongo también capicúa: 6006=77*78

Una simpática referencia a estas búsquedas la tienes en  http://www.worldofnumbers.com/consec.htm

 

CASO N(N+2)

Este caso lo podemos tratar de la misma forma que el anterior. Esta es la tabla que se puede construir con hoja de cálculo:

Es curioso el caso de los números formados por nueves. Estas igualdades son muy simples, pero ilustrativas:

9×(9+2)=99

99×(99+2)=9999

999×(999+2)=999999

9999×(9999+2)=99999999

También destaca el capicúa 191, que se convierte en otro capicúa: 191*(191+2)=36863

Están publicados los primeros valores de N en http://oeis.org/A028503 y algunas curiosidades en http://www.worldofnumbers.com/quapron.htm. En ellas se comprueba la pertenencia de 9, 99, 999, 9999,…

Una consecuencia inmediata de la forma de estos productos es que equivalen a un número cuadrado menos la unidad. Es fácil verlo: a(a+2)=a²+2a=(a+1)²-1. Se puede comprobar mentalmente con los primeros, o creando una columna nueva en la hoja de cálculo.

 

Caso N(N+3)

Finalizamos este tipo de producto con el caso de dos factores que se diferencian en tres unidades, es decir, N(N+3)

Aplicando los mismos criterios de búsqueda llegamos a la sucesión de palíndromos. Esta vez usaremos el siguiente código PARI:

ispalindromic(n) = my(d = digits(n)); Vecrev(d) == d

for(i=1,10^6,if(ispalindromic(i*(i+3)),print(i,"  ",i*(i+3))))

Los primeros valores de N y del palindrómico N(N+3) son

 

Si en el anterior caso destacábamos el caso de 9, 99, 999, aquí llama la atención el de 28, 298, 2998,…en los que se forman:

28*(28+3)=868

298*(298+3)=89698

2998*(2998+3)=8996998

Estos casos están publicados en http://oeis.org/A028553. En esa página se enlazan otras de         

Patrick De Geest que analizan estos casos y los siguientes, N(N+4), N(N+5), que no estudiaremos aquí.

Caso K(2K+1)

Con las mismas técnicas que los anteriores podemos investigar aquellos números de los que uno es el doble del otro más la unidad. Resultan estos casos:

Elegimos esta relación para ver si la cumplía algún número primo de Sophie Germain (https://es.wikipedia.org/wiki/N%C3%BAmero_primo_de_Sophie_Germain), pero solo hemos encontrado el par (5, 11) con producto capicúa 55.

Caso K*K

Es el caso de los cuadrados que son capicúas.

Son bastantes, y están publicados en http://oeis.org/A002778

 

Caso K*2K

Es como buscar los productos que son doble de un cuadrado. No aparecen tantos como era de esperar, ya que la siguiente tabla presenta los menores de 10^5:

Están publicados los resultados, pero no los valores de N, en http://oeis.org/A028985

En esa página se destaca que el número de divisores de estos resultados es impar

En efecto, la suma de divisores de un número tiene como fórmula

Si el resultado es el doble de un cuadrado, su descomposición factorial tendrá la forma

Todos los factores con exponente par producirán en la fórmula de arriba factores impares. Por ejemplo, 7⁴ produciría 1+7+7²+7³+7⁴, que es impar. Igual ocurre con el 2, que, por ejemplo, 2²=1+2+2², impar. Por último, el 2 que encabeza la expresión produciría el factor 1+2=3, luego todos los paréntesis de la fórmula serán impares, y con ellos el producto.

 

 

Sobreyecciones de {1, 2,…,n} sobre {1, 2,…n-1} – Unos números de Lah

 No hay que olvidar la Combinatoria. En las últimas entradas nos hemos dedicado más a propiedades numéricas, por lo que en esta, como cambio,  estudiaremos un tema de base combinatoria que desembocará en un caso concreto de números de Lah.

Si deseamos construir una aplicación sobreyectiva de un conjunto de n elementos sobre otro de n-1, debemos buscar un origen para cada elemento del segundo conjunto, pero siempre nos sobrará uno del primero, que habrá que asignarlo a un elemento imagen ya elegido, con lo que este poseerá dos orígenes.

Esta situación se entiende bien con el símil de cajas y bolas. Deseamos meter n bolas en n-1 cajas, de forma que todas las cajas tengan al menos una bola y que todas las bolas estén asignadas a alguna caja. Esto nos obliga a meter dos bolas en una caja concreta.

En la imagen observamos una aplicación sobreyectiva de los números {1, 2, 3, 4, 5} sobre las cajas {1, 2, 3, 4} En ella hemos tenido que hacer convivir el 3 y el 5 en una misma caja.

¿Cuántas formas existen de construir este tipo de aplicaciones? Con esta pregunta llegaremos a un caso particular de los llamados números de Lah, cuando el parámetro k es igual a 2

(Imagen tomada de https://en.wikipedia.org/wiki/Lah_number)

Deducción de la fórmula

Observemos lo que hemos hecho:

En primer lugar debemos llenar las cajas con una bola. Como tenemos 5 bolas para 4 cajas, las posibles elecciones serán variaciones sin repetición de 5 sobre 4, es decir, 5*4*3*2. Esas serían las formas de completar las cajas. Siempre nos sobrará una bola, que podemos asignar a una de las 4 cajas posibles, luego debemos multiplicar por 4 y quedaría 5*4*3*2*4. Si razonamos así, estaríamos contando estos casos como dobles. Por ejemplo, en la imagen, repetiríamos el razonamiento con el 3 y con el 5, con lo que habríamos contado 5*4*3*2*4=480, en lugar de los 240 que efectivamente existen, es decir, 5*4*3*2*4/2=4*5!/2

Generalizando: El número de aplicaciones sobreyectivas de {1,2…n} sobre {1, 2,…n-1} equivale a un caso concreto de números de Lah (cuando k=2) dado por la expresión

Estos números están publicados en http://oeis.org/A001286

1, 6, 36, 240, 1800, 15120, 141120, 1451520, 16329600, 199584000, 2634508800, 37362124800, 566658892800, 9153720576000, 156920924160000, 2845499424768000, 54420176498688000, 1094805903679488000, …

Entre ellos figura el 240 que hemos deducido para n=5: 4*5!/2=2*120=240

Para el caso de n=3 el número de aplicaciones sería 6. Representamos las cajas mediante paréntesis: (12)(3), (13)(2), (23)(1), (1)(23), (2)(13), (3)(12)

Hay que advertir que dentro de cada paréntesis no influye el orden.

La fórmula para Excel sería (N-1)*FACT(N)/2

Podemos deducir la fórmula con otro razonamiento: Se puede decidir antes de nada qué dos bolas comparten caja. Esta elección se hace mediante combinaciones sin repetición de n elementos tomados de 2 en 2, es decir n(n-1)/2. Una vez elegido el par, hay que asignarle una caja, y esto supone n-1 posibilidades, con lo que quedaría un total de n(n-1)/2*(n-1) casos. Así nos quedarán libres n-2 bolas y n-2 cajas. Entre ellas se pueden formar (n-2)! aplicaciones biyectivas, que completarían el proceso. En resumen, tendríamos n(n-1)/2*(n-1)*(n-2)!=(n-1)*n!/2, como ya sabíamos.

Una propiedad derivada

En el razonamiento anterior usamos la expresión n(n-1)/2 como número de combinaciones, pero también es un número triangular de orden n-1, que equivale a la suma de consecutivos 1+2+3+…+n-1, luego estos números también se pueden expresar como

Lo puedes ver en esta tabla de Excel:

La parte central coloreada representa el conjunto de términos del sumatorio. A la derecha figuran en negrita los números de Lah para k=2, suma de los anteriores, y a la izquierda los factoriales. De esta tabla se pueden extraer unas representaciones interesantes para los números de Lah que estamos estudiando. Te dejamos que lo deduzcas:

6=(1+2)*1*2

36=(1+2+3)*1*2*3

240=(1+2+3+4)*1*2*3*4

1800=(1+2+3+4+5)*1*2*3*4*5

15120=(1+2+3+4+5+6)*1*2*3*4*5*6

Queda atractivo.

 

Recurrencia

Finalizamos este estudio con una breve referencia a la generación de cada número respecto al anterior y al número de orden. No hay que razonar mucho para comprender que

Se puede reproducir esta generación escribiendo una columna de índices y aplicar esta fórmula en una segunda columna a partir del 1:

No importa que el factor multiplicador no sea entero, porque se compensa con los factores del anterior número de Lah (sabemos que el resultado ha de ser entero).

 

Números hexagonales (2)

 Después de estudiar la formación de los números hexagonales desde varios aspectos en la anterior entrada, es el momento de pasar a sus propiedades. Sólo se incluyen algunas seleccionadas, las más adecuadas para el nivel que desea tener esta entrada.

Otras propiedades

Los números hexagonales son el resultado de sumar los números del tipo 4k+1 a partir del 1.

En efecto:

H₁=1, H₂=1+5=6, H₃=1+5+9=15,…

En general, aplicando la fórmula para sumar progresiones aritméticas:

 

Los números hexagonales coinciden con el semiperímetro en las ternas pitagóricas primitivas en las que la hipotenusa es consecutiva con el cateto mayor.

(Ver http://oeis.org/A000384, comentario de Lekraj Beedassy)

En efecto, estas ternas se pueden representar como

(m²-n², 2mn, m²+n²,).

El primer lado y la hipotenusa no pueden ser consecutivos, pues su diferencia es al menos de dos unidades, luego si los hay son los dos últimos:

Si m²+n²-2mn=1, será (m-n)²=1 y m-n=1, n=m-1, porque n<m.

El perímetro es 2m(m+n) y el semiperímetro m(m+n)=m(2m-1), que es un número hexagonal.

Por ejemplo, en la terna (9, 40, 41) son consecutivos 40 y 41, el perímetro vale 90 y su mitad, 45, es un número hexagonal.

 

Descomposición en suma de cuatro hexagonales

Salvo unos pocos números (5, 10, 11, 20, 25, 26, 38, 39, 54, 65, 70, 114 y 130. Ver https://oeis.org/A007527), todos los demás se pueden expresar como suma de cuatro números hexagonales.

Lo comprobamos con nuestra herramienta Cartesius para el intervalo (100,110):

Hemos manipulado algo la imagen de Cartesius para eliminar columnas en blanco. Se ha añadido la opción del 0 para destacar los números que sólo necesitan dos o tres hexagonales, como el 106. Los demás necesitan cuatro hexagonales. Observamos en la columna de la derecha que varios números aparecen como resultado de sumas distintas. El 106, por ejemplo equivale a tres sumas distintas.

Incluimos el planteo. Aunque no hayas manejado esta herramienta lo entenderás:

xvar=100&110 ‘Recorremos desde 100 a 110

xtotal=4 ‘Son cuatro los sumandos

xt=1..9 ‘Cada sumando actúa sobre el intervalo (1,9)

xt=suc((n-1)*(2*n-3)) ‘Número hexagonal n-1 (para abarcar el cero)

suma=vx ‘La suma también va del 100 al 110

creciente ‘Para evitar repeticiones

 

Según MathWorld, Legendre demostró que todo número mayor que 1791 es una suma de cuatro números hexagonales, y Duke y Schulze-Pillot mejoraron esto a tres números hexagonales por cada entero suficientemente grande (https://mathworld.wolfram.com/HexagonalNumber.html)

 

Un número hexagonal equivale a la suma de un triangular con el mismo índice sumado con el triple del triangular anterior.

Es decir: Hx_n=T_n+3T_n-1

Dejamos como ejercicio la demostración algebraica, porque la imagen siguiente es bastante clarificadora. El primer triángulo tiene índice 5 y los otros tres, 4.

Si en la imagen separamos el lado de la izquierda, de cinco elementos, obtenemos esta otra equivalencia (Lekraj Beedassy)

Hx_n=n+4T_n-1

También es fácil de demostrar algebraicamente.

Los números hexagonales son permutaciones con repetición de 2n elementos  {0,1} en las que el 1 figure repetido dos veces.

Lo que estamos afirmando es la validez de esta fórmula (permutaciones con repetición o número binomial):

Con nuestra herramienta Combimaq hemos creado las permutaciones correspondientes al valor 15 del tercer hexagonal:

La puedes descargar desde

http://www.hojamat.es/sindecimales/combinatoria/herramientas/herrcomb.htm#combimaq

Hemos usado estas condiciones:

Es fácil su demostración algebraica:

 

La suma de los inversos de los números hexagonales equivale al doble del logaritmo neperiano de 2 (Vaclav Kotesovec, Apr 27 2016)

Finalizamos este recorrido por las propiedades de los números hexagonales aproximando la suma de sus inversos mediante hoja de cálculo. Se puede comprobar creando una columna con los números hexagonales, adosando junto a ella una columna de inversos y usando después la suma. Si deseas avanzar a miles de términos, es preferible la siguiente función:

Public Function sum_inv_hex(n)

Dim i, s

s = 0

For i = 1 To n

s = s + 1 / (i * (2 * i - 1))

Next i

sum_inv_hex = s

End Function

 

Su código se entiende fácilmente. Te puedes crear un esquema en el que escribas el número de términos y le apliques la función para comparar el resultado con 2LOG(2):

Una forma sencilla para comprobar esto se basa en nuestra hoja de cálculo “Visor de sucesiones”

(http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#visor)

Le escribimos la fórmula del inverso de un número hexagonal

Activamos el Visor y nos devuelve una aproximación a la suma:

Con esto finalizamos el tema.

 

Números hexagonales (1)

 Introducción

En la serie de este curso sobre números poligonales, esta entrada es posterior a la dedicada a los pentagonales. Por ello, en algunos temas remitiremos a estos números y puede ser aconsejable consultar las entradas correspondientes

http://hojaynumeros.blogspot.com/2020/11/numeros-pentagonales-1.html

http://hojaynumeros.blogspot.com/2020/11/numeros-pentagonales-2.html

Definición e inserción con los poligonales en general

Los números hexagonales se generan, como todos los poligonales, alineando los elementos en estructuras de este tipo adosadas en orden creciente, y compartiendo dos lados cada una con la anterior, como se puede ver en este esquema construido con Excel:

Se corresponde con el número hexagonal de índice 5, ya que se han adosado cuatro estructuras hexagonales además de la inicial de un solo elemento. Estos esquemas se conservan por su carácter histórico, pero varias de las propiedades que veremos más adelante podrían servir como definición además de la clásica.

Todos los números poligonales se pueden calcular con la siguiente fórmula (ver mi publicación “Números y formas”

http://www.hojamat.es/publicaciones/numform.pdf):

 

En nuestro caso k=6, lo que simplifica bastante la fórmula, que queda como

Nombraremos en toda la entrada el hexagonal de índice l como hx_l. Como estamos acostumbrados a escribir los índices como n, la fórmula quedaría:

Un sencillo cambio nos indica que un hexagonal coincide con un número triangular de índice impar:

Todo número hexagonal coincide pues con un triangular de índice 2n-1, es decir, impar. Los de índice par no pueden ser hexagonales.

Hace tiempo publicamos en este blog una entrada dedicada a estos triangulares de índice par. Por su interés, la enlazamos:

https://hojaynumeros.blogspot.com/2013/09/triangulares-de-lado-par.html

Los primeros números hexagonales son 1 , 6 , 15 , 28 , 45 , 66 , 91 , 120 , 153 , 190 , 231, 276, 325, 378, 435, 496 , 561 , 630, 703, 780, 861, 946 ...Esta sucesión está publicada en http://oeis.org/A000384

Sencillos cálculos revelan que todos son triangulares. Por ejemplo, 561=33*34/2.

Esta lista es fácilmente reproducible con hoja de cálculo, gracias a la sencillez de la fórmula n(2n-1):

Entre ellos figuran dos números perfectos, 6 y 28. En realidad, todos los perfectos son hexagonales, debido a su fórmula, que es del tipo n(2n-1):

P=2^k-1(2^k-1) = 2^k-1(2*2^k-1-1) 

 

Otras expresiones de los números hexagonales

a(n) = binomial(n+1,2) + 3*binomial(n,2).

No es difícil comprobar esta identidad, que usa números combinatorios:

Criterio para reconocer hexagonales

Si un hexagonal es un triangular de lado impar, nos servirá el criterio para triangulares, que es que ocho veces un triangular más la unidad ha de ser un cuadrado.

En esta imagen puedes comprobar que ocho triángulos de lado 4 (y diez elementos) se adosan dejando un hueco (el círculo verde):

Por tanto 8T+1 siempre es un cuadrado si T es triangular. En la entrada que dediquemos a ellos se verá con más detalle. Así que en un hexagonal también se tiene que cumplir con 8H+1. Si sumamos una unidad al lado del cuadrado de la imagen nos resulta 2n+2. Y si n ha de ser impar, tendremos 2(2k+1)+2=4k+4, que será entero si lo dividimos entre 4. En resumen, ha de ser un entero esta expresión:

Con esta expresión y nuestra función ESCUAD, (es cuadrado) obtenemos la función que caracteriza si un número es hexagonal y además nos devuelve su índice:

Function ordenhexagonal(n)

Dim a, b

 

b = 0

a = 8 * n + 1

If escuad(a) Then ‘Criterio del 8H+1

b = (Sqr(a) + 1) / 4 ‘Búsqueda del lado

If b <> Int(b) Then b = 0

End If

ordenhexagonal = b ‘Si no es hexagonal dará cero.

End Function

 

Con esta función puedes detectar hexagonales en cualquier intervalo. Por ejemplo, entre los últimos 20 años, 2016 fue el único hexagonal, con orden 32. En esta captura de Excel lo puedes comprobar:

Definiciones por recurrencia

Mediante sumas acumuladas

Si un número hexagonal coincide con un triangular determinado, valdrán las recurrencias para estos números. Sabemos que Hx_n=T_2n-1. Por tanto, si el triangular T_n-1 se convierte en el siguiente T_n sumándole su índice n-1, al hexagonal habrá que sumarle dos índices, 2n-2 y 2n-1, es decir, 4n-3. En efecto, si Hx₃=15, Hx₄=15+4*4-3=15+13=28, como bien podemos comprobar.

En esta tabla hemos escrito el primer 1 y después hemos ido añadiendo 4n-3:

Mediante recurrencia lineal

Jaume Oliver Lafont propone la siguiente en OEIS (adaptamos la escritura):

Hx(n) = 3*Hx(n-1) - 3*Hx(n-2) + Hx(n-3), Hx(0)=0, Hx(1)=1, Hx(2)=6.

La comprobaremos con nuestra hoja dedicada a las recurrencias lineales, en este caso de tercer orden (http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#recurre2)

Abrimos la hoja correspondiente al tercer orden y rellenamos los coeficientes 3, -3, 1 y los términos iniciales 0, 1, 6:

Pulsamos el botón de “Ver sucesión” y obtenemos una columna con los números hexagonales incluido el cero:

Es una simple curiosidad.

 

Uso de la calculadora “Calcupol”

En todas las entradas referidas a números poligonales nos referiremos a esta calculadora. Será inevitable repetir algunas instrucciones para cada tipo, pero el autor ignora en qué orden se pueden leer estas entradas, por lo que es preferible repetir a no explicar.

Si ya la conoces, puedes saltar estos párrafos.

Esta calculadora es una hoja de cálculo (En Excel o Calc) que puedes descargar desde mi página web:

http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/calcupol.xlsm

En primer lugar es conveniente poner la calculadora en modo poligonal y de orden 6:

Cálculo directo: Basta escribir (recuerda que todo va con el ratón) 6 POL y después el índice o longitud del lado (termina siempre con el signo =). Por ejemplo, si tecleas 6  POL  1  0  =   obtendrás el hexagonal número 10, que es el 190:

Identificación: Si ya has concretado Poligonal Orden 6, puedes usar la tecla  ES  para saber si un número es o no hexagonal. Escribe, por ejemplo, 946 y pulsa esa tecla ES

(puedes borrar pantalla con la tecla  CA )

Obtendrás una respuesta afirmativa

En pantalla aparecerá su índice

En efecto, Hx₂₂=946

Escribe otro número, por ejemplo 947, que no será hexagonal. En ese caso la respuesta será:

Próximo y anterior

Con las teclas   PROX  y  ANT  podemos recorrer todos los número hexagonales. Si tienes en pantalla 2000, al pulsar   ANT  obtendrás de nuevo 1891, que es el hexagonal más cercano a 2000 e inferior a él y si ahora usas  PROX  saltará al valor 2016, que es el siguiente hexagonal.

 En la siguiente entrada estudiaremos algunas propiedades curiosas de estos números.