Suma de los primeros primos y sus potencias (2)

En la anterior entrada sumamos números primos mediante funciones de Excel y Calc, PARI y el Buscador de Naturales. Ahora sumaremos potencias de primos. En este caso nos servirá la función sumprimoene de Excel, que suma las potencias de los primeros primos.

Suma de cuadrados de primos

La función sumprimoene permite sumar cuadrados de primos. El resultado es

Es un cálculo fácil y están publicados los resultados en http://oeis.org/A024450

4, 13, 38, 87, 208, 377, 666, 1027, 1556, 2397, 3358, 4727, 6408, 8257, 10466, 13275, 16756, 20477, 24966, 30007, 35336, 41577, 48466, 56387, 65796, 75997, 86606,…

Como simple curiosidad, y para un estudio más sencillo, este sería el planteamiento con el Buscador de Naturales:

La primera condición detecta cuadrados, la segunda obliga a que la base sea un número primo y la tercera suma. El resultado, como era de esperar, coincide con los anteriores:

Algunas propiedades

Los números primos pueden ser del tipo 4k+1 o 4k+3 (salvo el 2), pero sus cuadrados son siempre del tipo 4k+1, como se observa en estos desarrollos:

(4k+1)²=16k²+8k+1=4q+1

(4k+3)²=16k²+24k+9=4r+1

Esto hace que, al sumarlos, el 1 se vaya acumulando a 2, 3, 0, 1, 2…Los restos de estas sumas respecto al módulo 4 recorrerán el ciclo 0, 1, 2, 3…

Lo vemos en esta tabla, en la que hemos aplicado la función RESIDUO de Excel y Calc con módulo 4.

Así que cada dos sumas nos encontraremos con un número par, y cada dos ellos con un múltiplo de 4.

Si relacionamos los restos con los valores de N nos resulta:

Las sumas de orden 2n-1 son todas pares.

Las de orden 4n-3 son múltiplos de 4

De igual forma, sabemos que todos los primos son del tipo 6k+1 o 6k-1 (salvo el 2). Sus cuadrados serán:

(6k+1)² = 36k²+12k+1=12m+1

(6k-1)² = 36k²-12k+1=12m+1

Así que en cada sumando (salvo el primero, 4) recorrerá es sus restos respecto a 12 todos los valores desde 0 hasta 11. Lo puedes comprobar aquí:

De esta tabla se deduce que las sumas de orden 3n+1 son todas números múltiplos de 3, pues equivalen a 12m, 12m+3, 12m+6 o 12m+9.

Así podríamos ir descubriendo otras propiedades similares. Las tienes en la página http://oeis.org/A024450

Las demás sumas, como las del tipo 12k+7 pueden ser números primos. Vemos que es posible, que en la segunda columna de la siguiente tabla son todos primos.

En la tabla se observa algo esperable, y es que los restos módulo 12 solo pueden ser 1, 5, 7 y 11, aunque aquí no forman una sucesión periódica. También en los valores de N faltan los considerados en los párrafos anteriores, como 2n-1, 3n+1, 4n-3,…Es evidente que todos son pares.

Están publicados en http://oeis.org/A098562

Parece ser que el único cuadrado en la suma de cuadrados de primos es el 4 (conjetura). No se han encontrado cubos. De la sucesión de Fibonacci aparecen  13 y 377. De triangulares aparecen dos, 666 y 5022865. De oblongos no aparecen.

 

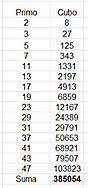
Suma de cubos de primos

Aquí no se esperan propiedades destacadas, pero lo intentamos.

Las primeras sumas de cubos de primos son del tipo:

(4k+1)³=64k³+48k²+12k+1=4m+1

(4k-1)³=64k³-48k²+12k-1=4m-1=4m+3

Los restos 1 y 3, al sumarse, producen todos los restos posibles: +1=2, 1+2=3, 1+3=0, 0+1=1,…Así, en la siguiente tabla aparecen todos los restos módulo 4:

Esto nos abre posibilidades de buscar primos y, ciertamente, se encuentran con relativa facilidad:

503, 15803, 35287433, 106954091, 3024050339, 3661922443, 7223017657, 10412687891, 11190761311, 12004517137, 25886083477, 36501131837,…

En este tema casi todo está ya publicado. Estos pertenecen a http://oeis.org/A066525 y no parecen tener propiedades interesantes.

 

 

 

Suma de los primeros primos y sus potencias (1)

En esta entrada y la siguiente vamos a trabajar un poco con las sumas de los primeros primos, y ampliaremos a alguna potencia. La idea es encontrar curiosidades o propiedades, así como la naturaleza de esas sumas.

Herramientas previas con Excel y Calc

Comenzamos con una función que sume potencias de los primeros primos:

Public Function sumprimoene(a, k) As Long

Dim prim, n, s As Long

prim = 2 ‘Primer primo

n = 1 ‘Contador

s = 2^k ‘Primera suma

While n < a

prim = primprox(prim) ‘A cada primo le encontramos el siguiente

n = n + 1 ’Se incrementa el contador

s = s + prim ^ k ‘Sumamos la potencia del primo

Wend

sumprimoene = s

End Function

Por ejemplo, con esta función obtenemos la suma de los cubos de los primeros 15 primos:

SUMPRIMOENE(15;3)=385054

Podemos comprobarlo con esta tabla:

Versión PARI

La función básica en PARI es similar. Hemos usado la siguiente función IS en los valores 15 (número de primos) y 3 (exponente):

is(a,k)={my(s=2^k,n=1,p=2);while(n<a,p=nextprime(p+1);n+=1;s=s+p^k);s}

print(is(15,3))

En la web de PARI/GP hemos introducido este código para comprobar el resultado

 

Versión elemental con el Buscador

Nuestro Buscador de Naturales (http://www.hojamat.es/sindecimales/divisibilidad/herramientas/herrdiv.htm#buscador) suma primos, y veremos en la siguiente entrada que también puede sumar potencias. Basta escribir la condición PRIMO y la de EVALUAR TOTALES. En la imagen figuran los primeros primos y sus sumas parciales:

El resultado es 160.

Suma de primos igual a un primo

La suma de los primeros primos puede ser también un número primo. El primer caso elemental, además del mismo 2, es el 2+3=5, y el siguiente, 2+3+5+7=17

Con la función ya explicada en VBA de Excel se puede establecer una búsqueda sencilla de primos que son suma de los primeros primos. El resultado es:

En la primera columna figura el número de primos sumados y en la segunda el primo resultante. Estos últimos están publicados en http://oeis.org/A013918

 

A013918              Primes equal to the sum of the first k primes for some k.                   

2, 5, 17, 41, 197, 281, 7699, 8893, 22039, 24133, 25237, 28697, 32353, 37561, 38921, 43201, 44683, 55837, 61027, 66463, 70241, 86453, 102001, 109147, 116533, 119069, 121631, 129419, 132059,

Nos vale en PARI el procedimiento publicado por Michael B. Porter en esa página:

n=0; forprime(k=2, 2300, n=n+k; if(isprime(n), print(n)))

Aquí aprovecha que forprime recorre los primos rápidamente.

Procedimiento con el Buscador

El carácter elemental de esta herramienta no permite bucles como los usados hasta ahora, pero una instrucción reciente nos permite visualizar los mismos resultados:

Indica que busquemos primos cuya suma sea también prima. Resulta:

Resalta en la lista los totales que son primos.

Otros resultados

La suma puedes ser un cuadrado, aunque no abundan los resultados.

Cuadrados

Procedimientos similares a los anteriores nos dan hasta seis soluciones. Por ejemplo, con PARI usamos

n=0; forprime(k=2, 2*10^6, n=n+k; if(issquare(n), print1(n,", ")))

Obtenemos cuatro fácilmente:

Están publicados en http://oeis.org/A061890

100, 25633969, 212372329, 292341604, 3672424151449, 219704732167875184222756

Como estamos comparando números de naturaleza distinta, no es fácil descubrir propiedades.

Triangulares

Para saber si un número T es triangular basta con exigir que 8*T+1 sea cuadrado. Corregimos el código PARI y queda:

n=0; forprime(k=2, 2*10^6, n=n+k; if(issquare(8*n+1), print1(n,", ")))

Lo ejecutamos en la web de PARI:

También están publicados:

http://oeis.org/A066527

A066527              Triangular numbers that for some k are also the sum of the first k primes.         

10, 28, 133386, 4218060, 54047322253, 14756071005948636, 600605016143706003, 41181981873797476176, 240580227206205322973571, 1350027226921161196478736

Otros ejemplos

De números oblongos solo hemos encontrado el 2 entre los menores de 2*10^7. De cubos, ninguno. De la sucesión de Fibonacci, tres: 2, 5 y 2584 (entre los menores de 7*10^7)

Es normal que no se encuentren muchos.

Números que son el doble de un cuadrado

Hoy haremos un ejercicio de “dar vueltas” a un tema, técnica muy usada en los primeros tiempos de este blog y que hemos ido abandonando a lo largo de sus temporadas. Consiste en tomar un concepto y buscarle propiedades desde varios puntos de vista.

Hoy daremos vueltas a los números que son el doble de un cuadrado, como 2, 8, 72 o 288. Su expresión es, evidentemente, D(n)=2n², donde los hemos representado con la D de doble. Simultáneamente, son mitad de otro cuadrado, ya que 2n²=(2n)²/2, lo que los convierte en el área de un triángulo isósceles de lado 2n, o de un cuadrado de diagonal 2n.

Es una expresión muy simple, pero que nos puede llevar a varios territorios muy diferentes entre sí.

Están publicados en http://oeis.org/A001105, y de esa página extraeeremos algunas ideas.

Relación con números figurados

Es evidente que estos números son también figurados (representables con una figura geométrica), como los triangulares o pentagonales, pero especiales, no pertenecientes a la categoría general de números poligonales. Simplemente están formados por dos cuadrados adosados, tal como se ve en la siguiente imagen.

Como todo cuadrado es suma de dos triangulares consecutivos, los dobles de cuadrados que estamos estudiando se podrán formar adosando cuatro triangulares:

En la imagen se han usado los triangulares T(4) y T(5) para formar el número 50=2*5²=2(T(4)+T(5))=2(10+15)=50

Por tanto, además de ser dobles de cuadrados, estos números son suma de dobles de triangulares, como era de esperar. Al contrario, también son mitad de una suma de triangulares consecutivos, según la figura siguiente:

Algebraicamente, podemos expresar:

Todo doble de cuadrado es el promedio de dos números triangulares consecutivos:

2n²=(T(2n-1)+T(2n))/2=(2n(2n-1)+2n(2n+1)/4=2n*4n/4=2n²

Es decir D(n)=(T(2n-1)+T(2n))/2

Así: 2=(1+3)/2, 8=(6+10)/2, 18=(15+21)/2

Como los números triangulares, multiplicados por 8 y aumentados en una unidad se convierten en cuadrados (8T(n)+1=(2n+1)²), como ocurre, por ejemplo, en 8*15+1=121=11², la propiedad anterior nos indica que si efectuamos la misma operación con los dobles de cuadrados, resultará el promedio de dos cuadrados:

8D(n)+1=(8T(2n-1)+1+8T(2n)+1)/2=((4n-1)²+(4n+1)²)/2

Ejemplo: 8*D(4)+1=8*32+1=257

(15²+17²)/2=(225+289)/2=514/2=257

Si a un doble de cuadrado lo multiplicamos por 8 y le añadimos una unidad, resulta el promedio de dos cuadrados diferenciados en dos unidades.

La anterior operación desemboca en un cuadrado más la unidad, ya que 8D(n)+1=16n²+1=(4n)²+1. Así ha ocurrido en el ejemplo anterior.

El cuadrado de un número múltiplo de 4 más la unidad es el promedio de dos cuadrados m² y (m+2)².

Por ejemplo, 1024+1=1025=(31²+33²)/2

Con esto finalizamos la “vuelta” a este tipo de números figurados y sus propiedades algebraicas.

Relación con sumas

D(n) es el resultado de sumar todas las particiones de 2n en exactamente dos partes(Wesley Ivan Hurt, Jun 01 2013).

Es sencillo demostrarlo, pues en cada paréntesis de los siguientes figura una partición de 2n:

(1+2n-1)+(2+2n-2)+…(n+n)=n*2n=2n²=D(n)

La suma de enteros consecutivos entre D(n) y D(n+1)-1, ambos inclusive, es un cubo (Patrick J. McNab, Dec 24 2016).

En efecto, entre 8 y 32, por ejemplo, esa suma es 8+9+10+11+…30+31, y es igual a 343=7³. En general:

Los primeros números consecutivos suman un triangular, luego esa suma será igual a S=T(D(n+1)-1)-T(D(n)-1). Desarrollando:

S=T(2(n+1)²-1)-T(2n²-1)=T(2n²+4n+1)-T(2n²-1) que es igual a

S=(2n²+4n+1)*(2n²+4n+2)/2-(2n²-1)*(2n²)/2.

Le damos este dato a Wolfram Alfha

Nos devuelve la expresión simplificada:

En efecto, es un cubo, (2n+1)³. Hemos programado estas sumas y se comprueba su carácter de cubo:

Recurrencias

Vincenzo Librandi propone la siguiente, en la que se mezcla a(n-1) con la variable n

a(n) = 4*n + a(n-1) - 2

No es difícil comprobarla con hoja de cálculo. Basta crear una columna con los valores 1, 2, 3, …y comenzar con a(1)=2, para después ir aplicando la relación hacia abajo:

Algebraicamente: 4n+2(n-1)²-2 = 4n+2n2-4n+2-2=2n²

Es preferible una recurrencia lineal homogénea, en la que a(n) depende de los términos anteriores sin implicar al número de orden. Muchos números figurados siguen una relación de recurrencia con los coeficientes 1, -3, 3, y en este caso es válida. Para demostrarlo hemos acudido a nuestra herramienta ecurecurre,xlsm, accesible desde la página

http://www.hojamat.es/sindecimales/otros.htm

En el listado sobre el blog que contiene hay que buscar ecurecurre.xlsm

Con ella se comprueba que los propuestos son los coeficientes válidos:

Para confirmarlo hemos acudido a otra de nuestras herramientas, la que estudia relaciones de recurrencia de segundo orden:

http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#recurre2

Al pedir la sucesión observamos que se reproduce la sucesión D(n):

2n² = 3(2(n-1)²))-3(2(n-2)²))+2(n-3)²

Volvemos a acudir a Wolfram Alfha y nos da la igualdad como verdadera.

 

Caso de base prima

Con nuestro Buscador de naturales

(http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#buscador)

 es sencillo crear la subsucesión de D(n) formadas por aquellos términos de base prima.

Forman la sucesión 8, 18, 50, 98, 242, 338, 578, 722, 1058, 1682, 1922, 2738, 3362, 3698, 4418,…

Está publicada en http://oeis.org/A079704

Los podemos representar como 2p²

En ellos, la falta de pautas en la sucesión de primos hace inviables las recurrencias lineales, pero presentan algunas curiosidades.

Funciones TAU, SIGMA y PHI

TAU (número de divisores) tiene le valor de 6 en todos los términos, porque depende solo de los exponentes, y según su fórmula, TAU(2p²)=(1+1)(1+2)=6

SIGMA (suma de divisores) posee un desarrollo parecido: SIGMA(2p²)=(1+2)(1+p+p²)

Por ejemplo,

SIGMA(242)=SIGMA(2*11²)=(1+2)(1+11+11²)=3*133=399

PHI (cuenta coprimos con N y menores que él), según también su fórmula usual, tendría en este caso la siguiente:

PHI(2p²)= 2p²(1-1/2)(1-1/p)=p(p-1)

En el caso de 98=2*7², se cumplirá PHI(98)=7*6=42

Podríamos seguir: OMEGA(2p²)=2, BIGOMEGA(2p²)=3, …