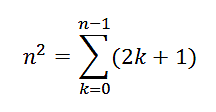Los números cuadrados (2)

Seguimos en esta segunda entrada dedicada a los números cuadrados con propiedades de recurrencia y relativas a sumas y las identidades entre ellas.

Recurrencias

Hay varios métodos recursivos para calcular números cuadrados. Ninguno es especialmente útil, y se presentan aquí como una curiosidad.

Suma de un impar

Es consecuencia de la definición como suma de impares, y es que al cuadrado anterior le sumamos el doble de su lado incrementado en una unidad. Por ejemplo, 7²+2*7+1=64=8²

Se puede plasmar en esta función recursiva de Excel:

Public Function cuadrado_r(n)

If n = 1 Then

cuadrado_r = 1

Else

cuadrado_r = 2 * n - 1 + cuadrado_r(n - 1)

End If

End Function

Funciona bien para números no muy grandes, pero puede fallar, por lo que la dejamos como una curiosidad.

Mediante los dos anteriores

C(n)=2C(n-1)-C(n-2)+2

Es fácil de demostrar: n²=2(n-1)²-(n-2)²+2=2n²-4n+2-n²+4n-4+2=n²

Así, de C(1)=1 y C(2)=4 obtenemos C(3)=2*4-1+2=9, C(4)=2*9-4+2=16,…

Recurrencia general para poligonales

Todos los números poligonales siguen la fórmula P(n,k)=3P(n,k-1)-3P(n,k-2)+P(n,k-3), que en nuestro caso quedaría como

C(n)=3C(n-1)-3C(n-2)+C(n-3)

Su ventaja radicaría en que usa cuadrados nada más, y no números aislados. Esto la convierte en una recurrencia de tercer orden homogénea, y la podemos tratar con nuestra hoja correspondiente:

http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#recurre2

Bastará dar como coeficiente 3, -3, 1 y como elementos iniciales 0, 1, 4:

Pulsando sobre el botón de “Ver sucesión” crearemos una columna de cuadrados,

 

Sumas

La suma de los primeros números cuadrados viene dada por una de las fórmulas de Faulhaber.

(ver https://es.wikipedia.org/wiki/F%C3%B3rmula_de_Faulhaber)

La correspondiente a los números cuadrados es la siguiente:

Es sencillo demostrarla por inducción completa. Aquí lo haremos restando la expresión correspondiente a n y la de n-1, para ver que el resultado es el nuevo cuadrado añadido. Así se ve en la calculadora Wiris:

Como curiosidad, aplicaremos nuestra herramienta de interpolación de Newton a las primeras sumas de cuadrados, 1, 5, 14, 30, 55…Es un tema complementario, que se puede ignorar:

Interpolación

Descargamos la hoja de interpolación desde

http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#newton

Escribimos las sumas en las celdas correspondientes:

Observamos que las diferencias de tercer orden son iguales (y la de cuarto es nula), lo que indica una función polinómica.

Leemos los coeficientes del polinomio:

Escribimos el polinomio con esos coeficientes, tal como se efectúa en la interpolación de Newton:

1+4*(X-1)+5/2*(X-1)*(X-2)+1/3*(X-1)*(X-2)*(X-3)

Como esta forma es poco legible, la simplificamos y factorizamos con Wiris:

Obtenemos la misma fórmula de Faulhaber. Aunque sea una mera curiosidad, es gratificante la coincidencia.

Teorema de los cuatro cuadrados

El teorema de los cuatro cuadrados de Lagrange establece que cualquier número entero positivo se puede escribir como la suma de cuatro o menos cuadrados perfectos. Tres cuadrados son suficientes para todos los enteros positivos salvo para números de la forma 4^k(8m+7). 

Un entero positivo se puede representar como una suma de dos cuadrados precisamente si su factorización prima no contiene potencias impares de primos de la forma 4 k + 3 (Fermat-Gauss). 

También se puede expresar todo cuadrado como suma de tres cuadrados con signo. Por ejemplo, 201221 se puede expresar con estas sumas:

201221 = 11^2+685^2-518^2

201221 = 9^2+679^2-510^2

201221 = 13^2+667^2-494^2

201221 = 5^2+589^2-382^2

La cercanía entre las bases de estos cuatro ejemplos sugiere que son un subconjunto de otro mucho más amplio.

Conseguir los cuatro cuadrados (o menos) en los que se descompone cualquier entero positivo requiere algoritmos que se ralentizan cuando ese entero es grande. Un algoritmo sencillo para Excel o Calc sería el de la siguiente función, que devuelve una solución, que no tiene que ser la óptima, pero que consta de cuatro cuadrados:

Function cuatrocuad$(n)

Dim i, j, k, l

Dim s$

Dim novale As Boolean

 

s$ = ""

novale = True

i = 0

While i <= n And novale ‘Primera base de cuadrado

j = 0

While j <= i And novale ‘Segunda base

k = 0

While k <= j And novale ‘Tercera base

l = n - i ^ 2 - j ^ 2 - k ^ 2  ‘Posible cuarta base

If l >= 0 And l <= k Then

If escuad(l) Then novale = False: s = s + Str$(i) + Str$(j) + Str$(k) + Str$(l) ‘Es una solución

End If

k = k + 1

Wend

j = j + 1

Wend

i = i + 1

Wend

If s = "" Then s = "NO"

cuatrocuad = s

End Function

 

Hay que insistir en que no devuelve la mejor solución, sino la que tiene las bases menores. Así, para 9, que es cuadrado, da la solución 2^2+2^2+1^2+0^2.

Hemos elegido un intervalo de enteros positivos al azar para una sencilla comprobación del teorema:

Observamos que tres números sólo necesitan tres cuadrados.

 

Identidades

Cuadrado de suma o diferencia

Aunque son de carácter elemental, no podemos olvidar aquí los cuadrados de sumas y diferencias:

Cercana a ellas es la identidad babilónica, fácil de deducir:

Identidad de Brahmagupta

En el apartado de sumas de cuadrados no puede faltar esta identidad, muy usada en cuestiones numéricas, y que se demuestra con un simple desarrollo algebraico:

En cualquier texto de Teoría de Números se puede encontrar un uso de esta identidad.

Identidad de Euler

Euler amplió esta idea a ocho cuadrados, según podemos observar en esta imagen tomada de la página de Wikipedia https://es.wikipedia.org/wiki/Identidad_de_los_cuatro_cuadrados_de_Euler

 

 

Los números cuadrados (1)

Primeras definiciones y propiedades

Incluimos aquí el estudio de los números cuadrados, considerándolos prioritariamente como números poligonales, y dejando como complementarias las cuestiones derivadas de su naturaleza como producto n*n.

Cuadrado como n*n

La primera idea que se tiene de los números cuadrados es que son el resultado de multiplicar un número entero por sí mismo: C=n*n (por eso, a la operación n² se le ha dado el nombre de elevar al cuadrado).

Se les llama también cuadrados perfectos. Este producto se puede representar como una matriz cuadrada de puntos.

Es conveniente disponer de un criterio para saber si un número es cuadrado. El más fiable es el de descomponer el número en factores primos y observar si todos los exponentes son pares. Esto es así porque si un número primo p divide a un cuadrado, p² también lo divide.

Así se evitan los decimales que aparecen en otros criterios. El inconveniente radica en la programación de la extracción de factores. En el otro extremo de la definición encontramos los números libres de cuadrados, en los que todos los exponentes son impares.

Un criterio menos fiable es el de sacar la raíz cuadrada, tomar su redondeo a un número natural o su parte entera (llamada raíz cuadrada entera) y ver si al elevarla al cuadrado reconstruye el número inicial. Así se procede en esta función:

Public Function escuad(n) As Boolean

If n < 0 Then

escuad = False

Else

If n = Int(Sqr(n)) ^ 2 Then escuad = True Else escuad = False

End If

End Function

En lenguajes avanzados de programación se dispone ya de una función issquare o similar.

Esta definición permite considerar que un número cuadrado puede terminar solo con las cifras 0, 1, 4, 5, 6 o 9 en el sistema de numeración decimal. Es fácil comprobarlo multiplicando números por sí mismos. Así que un número que termine en 2, 3, 7, 8 no será cuadrado.

Esta definición de cuadrado también nos lleva a que tendrá un número impar de divisores. Si todos los exponentes de factores primos son pares, el número de divisores será un producto de impares, y por tanto impar. Puedes revisar esta idea en nuestro documento http://www.hojamat.es/sindecimales/divisibilidad/teoria/teordivi.pdf

Aquí tienes un volcado del párrafo en el que se desarrolla la fórmula correspondiente:

Este sería un buen criterio para detectar si un número es cuadrado, pero resulta largo y lento.

Cuadrado como número poligonal

La construcción de un cuadrado siguiendo los procedimientos generales de construcción de poligonales nos llevaría a un esquema como el de la imagen:

 

En ella observamos sin dificultad que el número cuadrado n² es la suma de los primeros números impares: 1+3+5+7+9=25=5²

El caso general se demuestra por inducción completa:

Si n² equivale a la suma

(2*0+1)+(2*1+1)+(2*2+1)+(2*3+1)+…+(2*(n-1)+1),

el siguiente cuadrado, (n+1)² es igual a n²+(2*n+1), lo que completa la suma de impares.

Así que se cumple

 Sumas de números impares consecutivos

Una consecuencia de esta propiedad es la de que cualquier suma de números impares consecutivos equivale a la diferencia entre dos cuadrados. Por ejemplo, la suma 55+57+59+…+87+89+91 se puede calcular como la diferencia entre estas dos sumas:

(1+3+5+7+…+91)-(1+3+5+7+53)=46^2-27^2

El 46 y el 27 se obtienen teniendo en cuenta, según la fórmula anterior, que los sumandos tienen la forma 2k+1.

Si se toman dos sumandos impares consecutivos, el resultado será un cuadrado par 2n*2n=4n², pues

Si multiplicamos dos números pares (o impares) consecutivos y añadimos una unidad obtenemos también un cuadrado, pues n(n+2)+1=n²+2n+1=(n+1)²

 

Cuadrado como suma de dos triangulares

Otra generación de cuadrados viene dada, tal como vimos en el tema correspondiente, como suma de dos triangulares consecutivos. En la imagen se observa que el cuadrado 25 es la suma de los triangulares 10 y 15.

Como un triangular es un número combinatorio, esta propiedad se puede expresar como (elegimos el símbolo C(n) para representar el cuadrado de orden n):

Desde el punto de vista de los cuadrados esta relación no tiene más interés.

Cuadrado como suma de OBLONGO(N)+N+1

Otra relación que se queda en simple curiosidad es que si a un oblongo le añadimos su lado mayor, se convierte en un cuadrado.

En efecto, los oblongos vienen dados por la expresión n(n+1), y si le sumamos n+1 se convierte en n(n+1)+(n+1)=(n+1)(n+1)=(n+1)²

Esta propiedad es más sugestiva si se expresa al revés: si a un conjunto cuadrado le eliminas un lado, se convierte en oblongo.

Si al cuadrado 64 le quitamos un lado (8) nos queda 56, que es oblongo, por ser 7*8.

 

Una curiosidad

Copiamos un texto publicado por Amarnath Murthy, Mar 24 2004en la página de OEIS:

Begin with n, add the next number, subtract the previous number and so on ending with subtracting a 1: a(n) = n + (n+1) - (n-1) + (n+2) - (n-2) + (n+3) - (n-3) + ... + (2n-1) - 1 = n^2.

Como invitación a demostrarlo, insertamos ese proceso aplicado al número 12:

En la primera columna se sitúan los números consecutivos a 12 y en la segunda los anteriores. Se suman y se restan unos de otros, resultando al final 144=12².

Números de Zumkeller(2) – Otros métodos de búsqueda

En la entrada anterior se diseñó un esquema de cálculo para encontrar las particiones de igual suma, típicas de los números de Zumkeller. El procedimiento, algo lento, consistía en escribir los divisores de un número en columna, acompañarlos sucesivamente con las expresiones binarias de los números 1 a 2^TAU-1 y mediante multiplicaciones, conseguir todas las particiones entre divisores:

Se afirmó en la entrada anterior que este esquema, para valores de TAU superiores a 10 o 12, era bastante lento, pero existe una forma de simplificarlo un poco. La idea es que el número estudiado entrará, con toda seguridad, en una de las dos particiones, y acompañado, en general, por menos sumandos que en la otra partición.

Lo explicamos con el desarrollo para 204, cuya factorización es 3*2²*17, lo que asegura que es un número de Zumkeller. Sus particiones de igual suma son:

Total divisores: 1+2+3+4+6+12+17+34+51+68+102+204=504

Primera partición: 1+3+4+6+17+51+68+102=252

Segunda partición: 2+12+34+204=252

Los divisores han sido 1, 2, 3, 4, 6, 12, 17, 34, 51, 68, 102, 204

Si observamos la partición más corta, es claro que los sumandos compañeros de 204 no pueden superar la diferencia 252-204=48. Esto excluye a los divisores 51, 68, 102 y el mismo 204. Podríamos entonces cambiar los datos del problema:

• ·       Los divisores podrían ser 1, 2, 3, 4, 6, 12, 17, 34
• ·       La suma no tendría que ser 252, sino 48
• ·       El valor real de TAU, que era de 12 divisores, se puede reducir a 8.

Hemos implementado una segunda hoja en nuestra herramienta http://www.hojamat.es/blog/zumkeller.xlsm duplicando el algoritmo, pero con estas modificaciones. El resultado, en el caso de 204 quedaría así:

Observamos que el valor de TAU ha quedado en 8, por haber eliminado cuatro divisores, 51, 68, 102 y 204 (tres de ellos han quedado como residuales en la parte baja del esquema). También cambia el valor de la suma, que ahora es de 48, y, si observamos las columnas que crean particiones, tan solo llegan hasta el número 34.

Con estos cambios, la velocidad de proceso aumenta, más o menos según la factorización. En el resultado obtenido, la partición que nos interesa es la de menor número de sumandos. En este caso tendríamos:

Total divisores: 1+2+3+4+6+12+17+34=48                         

Primera partición: 1+3+4+6+17=48                            

Segunda partición:  2+12+34=48                      

Si a la segunda partición le añadimos el 204 obtendremos la solución del primer algoritmo:

2+12+34+204=252

Uso de nuestra herramienta “Cartesius”

Esto que sigue es una curiosidad, de la que se puede prescindir. Lo que tiene de importante es que nos puede devolver más de una solución a las particiones de igual suma.

En una entrada nuestra de hace unos cinco años, explicábamos el uso de Cartesius para lograr particiones.

(https://hojaynumeros.blogspot.com/2017/06/cartesius-5-particiones-1.html)

Esta herramienta puedes descargarla desde

http://www.hojamat.es/sindecimales/combinatoria/herramientas/herrcomb.htm#cartesius

En la entrada referida se recomendaba este planteo para lograr una partición concreta, la del 7 en todos sus sumandos posibles:

XRANGO=7

XT=1..7

SUMA=7

CRECIENTE

 

Con algo de lentitud, crea todas las particiones del 7:

Siguiendo las reflexiones de los párrafos anteriores, si elegimos, por ejemplo, el número 60=2*2*3*5, su TAU es igual a 12, y podríamos rebajarla a 10, porque la mitad de sigma es, en este caso, 84. Si le restamos el número 60 nos queda 24, y podemos eliminar los divisores 30 Y 60, con lo que nos quedaría:

• Divisores válidos: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20
• Nueva TAU: 10
• Suma exigida: 24

El planteo adecuado en Cartesius sería

XRANGO=10

XT=1,2,3,4,5,6,10,12,15,20

SUMA=24

CRECIENTE

De esta forma, con bastante lentitud, obtenemos dos soluciones en lugar de una:

Las particiones de igual suma podrían ser

Primera partición: 1+2+3+5+6+10+12+15+30=84              

Segunda partición: 4+20+60=84   

Y también

Primera partición: 3+4+5+10+12+20+30=84             

Segunda partición: 1+2+ 6+15+60=84

Ya se dijo que es una curiosidad, porque la falta de velocidad del proceso no compensa su utilidad, salvo que busquemos números de Zumkeller con varias soluciones.