En muchas ocasiones puede interesar sumar las primeras potencias de los números naturales. Están publicados todos los casos populares, como sumas de cuadrados o de cubos, y existe una fórmula, atribuida a Faulhaber, que nos da el resultado para cualquier exponente. En el siguiente recorte de Wikipedia puedes estudiarla.
https://es.wikipedia.org/wiki/F%C3%B3rmula_de_FaulhaberEl problema que tiene esta fórmula para un uso elemental
es que requiere conocer los números de Bernouilli.
El procedimiento que explicaremos a continuación es una
alternativa para encontrar el valor de la suma de una sucesión de potencias o
expresiones polinómicas con Excel o Calc. Se debe tomar como un simple
entretenimiento, aunque en algunas situaciones puede resultar útil.
Un
ejemplo: Cuadrados de oblongos:
Explicamos el procedimiento con un ejemplo, como sería
encontrar una fórmula para la suma de los cuadrados de los primeros oblongos,
es decir de la expresión n2(n+1)2.
A)
Creamos la sucesión:
Con las hojas de cálculo es muy fácil encontrar las
primeras sumas de cualquier sucesión. En este caso hemos ido creando columnas
para N(N+1), que son los oblongos, sus cuadrados N2(N+1)2
y sus sumas sucesivas.
Con esto ya sabemos que la sucesión 4, 40, 184, 584,
1484, 3248, 6384,…es la que requiere una fórmula similar a las de Faulhaber.
Para continuar debemos basarnos en dos conjeturas:
1) La fórmula buscada creemos que será de tipo polinómico.
2) Intuiremos de alguna forma qué grado puede tener ese
polinomio. Esta segunda no es tan importante, pero nos ayudará en el siguiente
paso.
B)
Aplicamos la interpolación de Newton:
La búsqueda de una fórmula polinómica que resuma un
conjunto de valores es una interpolación. Disponemos de una hoja de cálculo que
encuentra esa fórmula para los valores 1, 2, 3, 4,…mediante la interpolación de
Newton:
http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#newton
(Ver https://es.wikipedia.org/wiki/Interpolaci%C3%B3n_polin%C3%B3mica_de_Newton)
Este método se adapta bien a la estructura de Excel y
Calc. En nuestra hoja basta escribir los primeros términos y observar las
diferencias que se producen. Conviene usar todos los que entren en el esquema
(máximo 7). Si se conoce el grado del polinomio, se pueden usar menos. Esta
sería la situación para el caso de cuadrados de oblongos:
Estos coeficientes actúan sobre los polinomios 1, (x-1),
(x-1)(x-2), (x-1)(x-2)(x-3),…y esa es la mayor dificultad de esta
interpolación, porque el resultado en este caso sería
4+36*(x-1)+54*(x-1)*(x-2)+74/3*(x-1)*(x-2)*(x-3)+4*(x-1)*(x-2)*(x-3)*(x-4)+1/5*(x-1)*(x-2)*(x-3)*(x-4)*(x-5)
(Ya se han simplificado los coeficientes)
C)
Desarrollamos el polinomio interpolador:
Este resultado podría ser descorazonador, pero para su
simplificación contamos con los programas CAS ((Computer Algebra System) En
este blog se suele usar la Calculadora Wiris, gratuita y extendida en la
enseñanza.
Copiamos nuestra monstruosa fórmula en ella y pulsamos
sobre el signo =
Ya hemos conseguido el objetivo: la suma de los cuadrados de los oblongos sigue la fórmula x5/5+x4+5/3x3+x2+2/15x
Sustituimos el polinomio en la tabla para comprobar
Luego la fórmula queda:
La podemos factorizar con Wiris:
Estas son las etapas del proceso. Nos basamos en Excel y Calc, en nuestra hoja de interpolación y en un CAS. En la mayoría de los casos obtendremos el polinomio adecuado. Puede que el grado requerido sea mayor, con lo que habría que ampliar el esquema de cálculo, pero ese trabajo es algo complejo.
Repetimos el trabajo con oblongos, Lo dejamos con
redacción escueta:
Sumas
de oblongos
Debemos buscar una fórmula para 2, 8, 20, 40, 70, 112, …
Interpolamos
Observamos que son nulas las diferencias a partir de la
cuarta, luego obtendremos un polinomio de tercer grado. Sería este
2+6*(x-1)+3*(x-1)*(x-2)+1/3*(x-1)*(x-2)*(x-3)
Con
wiris
Factorizando con la misma calculadora:Luego es el doble del combinatorio C(x+2,3), como puede verse en http://oeis.org/A007290
En este caso nos hemos limitado a comprobar, porque esta
suma ya está resuelta.
Como un ejemplo del uso de esta fórmula puedes distraerte
con mi entrada
http://hojaynumeros.blogspot.com/2018/09/suma-de-numeros-oblongos-consecutivos.html
Suma de potencias cuartas
Por último, reproduciremos una de las fórmulas más
conocidas de Faulhaber, la que suma potencias cuartas.
(Fuente: Wikipedia)
Seguimos los pasos sugeridos.
Construimos la sucesión:
Como sabemos que el grado de la fórmula de Faulhaber es 5, interpolaremos con al menos seis elementos.
Interpolación
A partir de los coeficientes de abajo construimos el
polinomio:
1+16*(x-1)+65/2*(x-1)*(x-2)+55/3*(x-1)*(x-2)*(x-3)+7/2*(x-1)*(x-2)*(x-3)*(x-4)+1/5*(x-1)*(x-2)*(x-3)*(x-4)*(x-5)
Simplificamos con Wiris
Si reducimos todo a denominador 30, coincidirá con la fórmula de Faulhaber correspondiente.





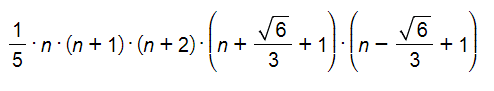








No hay comentarios:
Publicar un comentario