Escaladas de Conway

El año pasado, 2017, se notificó que una conjetura de Conway, conocida como “escalada a un primo” había resultado ser falsa. Tienes la noticia, comentarios y contraejemplos en estos dos blogs:

http://francis.naukas.com/2017/06/14/contraejemplo-a-una-conjetura-de-conway-sobre-los-primos/

https://www.gaussianos.com/la-conjetura-de-la-escalada-hasta-un-primo/

Si los has leído (y si no, te bastará con mi explicación) entenderás que el proceso que propone Conway es el de descomponer el número en sus factores primos agrupados con exponentes y ordenados en orden creciente, como 144=2⁴*3², y después escribir seguidos y mezclados bases y exponentes de las potencias resultantes (2432).

Si un número primo está elevado a la unidad, esta se ignora y no se añade al nuevo número.

Si llamamos f(n) a esa función obtendremos:

f(144)=2432

La idea de Conway es la de ir reiterando esta función hasta llegar a un número primo p, en el que es evidente que f(p)=p, dando fin al proceso.
En el caso del 144:

F(144)=2432, f(2432)=2719, que es primo y con él termina el proceso.

Los dos blogs citados te darán más detalles. Nuestro objetivo en esta entrada es conseguir el algoritmo con el Visual Basic de las hojas de cálculo. Es, por tanto un interés operativo más que matemático.

Función fconway(n)

A continuación se inserta el listado para hoja de cálculo de la función de Conway, pero antes hay que acudir a la función ajusta(n), que elimina del número n los espacios en blanco que Excel o Calc añaden a los números naturales. Su código es el siguiente:

Function ajusta$(a)
Dim d$

d$ = Str$(a) ‘Convierte el número en un string
While Left$(d$, 1) = " " ‘Mientras esté precedido de un espacio, este se elimina
d$ = Right$(d$, Len(d$) - 1) ‘Se corta el string desde su segundo carácter
Wend
ajusta$ = d$
End Function 

Una vez contamos con esta función, se tratará ahora de descomponer el número en factores y concatenar factores primos y exponentes, eliminando aquellos iguales a la unidad. Puede ser así:

Public Function fconway(n)

Dim primo(20), expo(20), numomega ‘Reservamos 20 memorias para primos y exponentes
Dim s$
Dim f, a, e, i


a = n ‘Recibimos n en la variable a
f = 2: i = 0: numomega = 0 ‘numomega es el número de primos
While f * f <= a ‘Vamos extrayendo primos hasta la raíz cuadrada de a
e = 0
While a / f = Int(a / f)
e = e + 1 ‘Se toma nota del exponente, que va creciendo
a = a / f ‘Se elimina el factor primo encontrado
Wend
If e > 0 Then ‘Se incorpora el nuevo primo con su exponente a las memorias
numomega = numomega + 1
primo(numomega) = f
expo(numomega) = e
End If
If f = 2 Then f = 3 Else f = f + 2 ‘Se avanza en posibles primos
Wend
If a > 1 Then ‘Se recoge el último primo
numomega = numomega + 1
primo(numomega) = a
expo(numomega) = 1
End If
s$ = "" ‘Construimos la concatenación de primos y exponentes mayores que 1
For i = 1 To numomega
s$ = s$ + ajusta(primo(i)) ‘Se incorpora el primo
If expo(i) > 1 Then s$ = s$ + ajusta(expo(i)) ‘Se añade el exponente si es mayor que 1
Next i
fconway = Val(s$) ‘Convertimos el string en número
End Function

Si escribimos un número cualquiera (en los blogs citados no se recomienda usar el 20) en una celda de Excel y tenemos implementada la función anterior (debes entrar en Programador – VisualBasic. Puedes consultar http://hojamat.es/guias/descubrir/htm/macros.pdf), podemos calcularla en la celda inferior, y después extenderla hacia abajo hasta que el resultado se repita o alcancemos una magnitud para la que Excel pasa a notación científica. Puedes ver algún ejemplo en la imagen:

En el primero, se alcanza el primo inmediatamente. En el segundo, al segundo intento, como ya vimos más arriba. El siguiente sobrepasa la capacidad de Excel, y el cuarto llega al primo en cinco pasos.

Podemos convertir este proceso en una función, pero si llegamos a los límites de Excel habrá que devolver un valor que lo indique, como podría ser el cero. Hemos diseñado esta:

Public Function finconway(n)
Dim a, b

a = 1: b = n ‘Usamos dos variables para cada iteración
While a <> b And a < 100000000000# And a > 0 ‘Límites de la iteración
a = b ‘Guardamos b en la variable a
b = fconway(b) ‘Avanzamos un paso en la iteración
If a >= 100000000000# Then a = 0 ‘Si el número es muy grande, lo hacemos cero
Wend
finconway = a
End Function

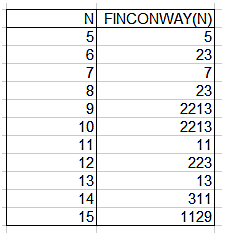
Con esta función se resuelve rápidamente el ascenso a primo. Aquí tienes los resultados desde 5 hasta 15, por ejemplo:

Esta función, aplicada al 542, devolvería un 0, ya que sobrepasa el límite de Excel para la escritura de todas las cifras. Este inconveniente se salva usando otro lenguaje. Hemos adaptado y completado la función en PARI incluida en la sucesión http://oeis.org/A080670 para definir la función finconway en ese lenguaje. Su código es:

fconway(n)=if(n>1, my(f=factor(n), s=""); for(i=1, #f~, s=Str(s, f[i, 1], if(f[i, 2]>1, f[i, 2], ""))); eval(s), 1)
finconway(n)=my(a=1,b=n);while(a<>b&&a>>0,a=b;b=fconway(b));a

Con ella es fácil reproducir los resultados de la tabla anterior:

Con el lenguaje PARI sí podemos encontrar el primo al que llegan las iteraciones con inicio en 542. Sería 131811420855589. En la imagen se puede observar cómo lo presenta PARI:

La conjetura

Si has leído las entradas de blog recomendadas más arriba, sabrás que existe un contraejemplo en el que la iteración no asciende a un primo, sino a un compuesto. Se trata del valor 13532385396179=13*532*3853*96179

Con nuestra función en PARI se detecta su invariancia en la iteración:

fconway(n)=if(n>1, my(f=factor(n), s=""); for(i=1, #f~, s=Str(s, f[i, 1], if(f[i, 2]>1, f[i, 2], ""))); eval(s), 1)
finconway(n)=my(a=1,b=n);while(a<>b&&a>>0,a=b;b=fconway(b));a
print(finconway(13532385396179))

En la imagen observamos que el resultado es el mismo valor:

Con esto terminamos, ya que el único objetivo era usar medios elementales para reproducir los ascensos a primo de Conway y el contraejemplo descubierto recientemente.