Esta es nuestra tercera entrada sobre números piramidales de cuatro dimensiones.
Puedes leer las anteriores en
http://hojaynumeros.blogspot.com.es/2017/11/numeros-piramidales-de-cuatro.html
y
http://hojaynumeros.blogspot.com.es/2018/01/piramides-cuadrangulares-en-cuatro.html
Hoy nos dedicaremos a los pentagonales y hexagonales. Seguiremos los mismos procedimientos para descubrirlos, ya que se desprenden directamente de la definición.
Generación directa
Partimos de los piramidales pentagonales de tres dimensiones:
1, 6, 18, 40, 75, 126, 196, 288, 405, 550, 726, 936, 1183, 1470, 1800, 2176, 2601, 3078, 3610, 4200, 4851, 5566, 6348, 7200, 8125,…
http://hojaynumeros.blogspot.com.es/2017/06/numeros-piramidales-4-pentagonos.html
Como en casos anteriores, construimos las sumas parciales: 1, 1+6=7, 1+6+18=25, 1+6+18+40=65,…y obtenemos:
1, 7, 25, 65, 140, 266, 462, 750, 1155, 1705, 2431, 3367, 4550, 6020, 7820, 9996, 12597, 15675, 19285, 23485, 28336, 33902,…
Estos serán, pues los piramidales pentagonales de cuatro dimensiones. Los puedes estudiar en
http://oeis.org/A001296
Expresión algebraica
Lo que sigue lo hemos aplicado en bastantes números figurados, por lo que simplificaremos las explicaciones. En primer lugar, abrimos nuestro interpolador para números naturales
http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#newton
Escribimos en él los primeros términos de la sucesión que hemos formado.
Leemos los coeficientes de (x-1), (x-1)(x-2), (x-1)(x-2)(x-3),…y formamos el polinomio interpolador, que según la anulación de diferencias quintas, será de cuarto grado:
1+6*(x-1)+6*(x-1)*(x-2)+10/6*(x-1)*(x-2)*(x-3)+3/24*(x-1)*(x-2)*(x-3)*(x-4)
Lo simplificamos en la página de WolframAlpha y obtenemos
Expresión que coincide con una de las contenidas en https://oeis.org/A001296
Son números de Stirling
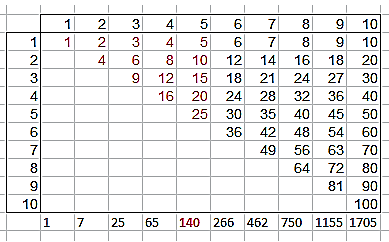
Los pentagonales que estamos estudiando son un caso particular de los números de Stirling de segunda clase para los índices (n+2,n), como puedes ver en los elementos subrayados de nuestra tabla
(La tienes alojada en http://www.hojamat.es/sindecimales/combinatoria/herramientas/herrcomb.htm#nume)
Si deseas conocer mejor estos números puedes acudir a
https://es.wikipedia.org/wiki/N%C3%BAmeros_de_Stirling_de_segunda_especie
Relación con números triangulares
En https://oeis.org/A001296 figura una propiedad interesante, debida a Jon Perry, y es que cada número piramidal pentagonal de cuatro dimensiones es suma de números triangulares multiplicado cada uno por su número de orden, es decir:
Esto se cumple para los primeros términos. Si tomamos los triangulares 1, 3, 6, 10, 15,…y formamos las sumas 1*1=1, 1*1+2*3=7, 1*1+2*3+3*6=25, 1*1+2*3+3*6+4*10=65,…y comprobamos que se cumple para los primeros términos. Acudimos a la inducción completa.
Bastará demostrar que PIR5_4(n+1)-PIR5_4(n) = (n+1)*T(n+1). En efecto, es cuestión de Álgebra:
PIR5_4(n+1)-PIR5_4(n)=((n+1)(n+2)(n+3)(3(n+1)+1)-n(n+1)(n+2)(3n+1))/24
Simplificamos y queda:
PIR5_4(n+1)-PIR5_4(n)=(n+1)(n+2)(12n+12)/24=(n+1)(n+1)(n+2)/2=(n+1)T(n+1)
Luego la propiedad es extensible a todos los términos.
En la misma página de OEIS, J. M. Bergot interpreta esta propiedad como la suma de todos los productos de dos elementos del conjunto {1, 2, …, n} tomados de todas las formas posibles, sin tener en cuenta el orden). Por ejemplo, 1*1 + 1*2 + 1*3 + 2*2 + 2*3 + 3*3 = 25.
Es sencillo de comprender, ya que si desarrollamos la suma de cada triangular por su número de orden, basta recordar que cada triangular es suma de números consecutivos, luego la suma queda:
1*T(1)+2*T(2)+3*T(3)+4*T(4) = 1*1+2(1+2)+3*(1+2+3)+4*(1+2+3+4)+…
Se ve que en la suma están contenidos todos los productos de cada número natural por sus precedentes, tal como afirma J. M. Bergot.
Es un buen ejercicio de hoja de cálculo construir una tabla que refleje este resultado. Hay que manejar bien las referencias absolutas y relativas. Un buen ejercicio de aprendizaje.
En la tabla que hemos construido se destaca el conjunto de sumandos que forman el piramidal pentagonal 140:
Piramidales hexagonales
Según nuestra política de no cansar con los temas, a los piramidales hexagonales les dedicaremos menos espacio y con ellos terminaremos el recorrido por los que tienen cuatro dimensiones.
Las operaciones que hay que realizar son:
(1) Acumulación de piramidales hexagonales de tres dimensiones
Partimos de los piramidales hexagonales de tres dimensiones:
1, 7, 22, 50, 95, 161, 252, 372, 525, 715, 946, 1222, 1547, 1925, 2360, 2856, 3417, 4047, 4750, 5530, 6391, 7337, 8372,…
(Ver http://hojaynumeros.blogspot.com.es/2017/07/numeros-piramidales-5-hexagonos.html)
Los acumulamos en sumas parciales:
1, 1+7=8, 1+7+22=30, 1+7+22+50=80,…
Nos resultarán así los números piramidales hexagonales de cuatro dimensiones:
1, 8, 30, 80, 175, 336, 588, 960, 1485, 2200, 3146, 4368, 5915, 7840, 10200, 13056, 16473, 20520, 25270, 30800,…
Los tienes publicados en http://oeis.org/A002417
(2) Obtención de la fórmula algebraica
También para estos números usamos nuestro interpolador
http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#newton
Como ya lo hemos desarrollado para otros tipos de números, sólo insertaremos el volcado de pantalla:
Como en otras ocasiones, observamos la anulación de las diferencias quintas y copiamos los coeficientes del polinomio en la parte inferior.
1+7*(x-1)+15/2*(x-1)*(x-2)+13/6*(x-1)*(x-2)*(x-3)+4/24*(x-1)*(x-2)*(x-3)*(x-4)
Simplificamos la expresión en la página de WolframAlpha y nos devuelve cuatro variantes:
Aunque la cuarta es la más sintética a efectos de cálculo, nos quedamos con la primera, porque se puede interpretar en términos de número combinatorio:
Una curiosa propiedad
Según un comentario de Floor van Lamoen en la página OEIS donde vienen publicados, se cumple que PIR6_4(n) es la suma de todos los números que no pueden expresarse de la forma t*(n+1) + u*(n+2) con t, u enteros no negativos. Desconocemos la demostración de este hecho, pero nos va a servir para repasar unos conceptos que desarrollamos en una entrada de este blog
http://hojaynumeros.blogspot.com.es/2010/02/frobenius-y-los-mcnuggets.html
Según el vocabulario introducido en esa entrada, lo que afirma Floor van Lamoen es que los números que estamos estudiando son suma de aquellos que no son representables respecto al conjunto {n+1,n+2}. En la entrada citada llamábamos número de Frobenius al máximo número no representable para un conjunto. En el caso de dos números coprimos a y b, ese número equivale a a*b-a-b. Esto nos garantiza que la suma de no representables es finita, y que, por tanto, puede coincidir con un número de nuestra lista.
En este caso particular, el número de Frobenius para {n+1,n+2} será
(n+1)*(n+2)-(n+1)-(n+2)=n^2+n-1
En el caso de n=7, ese número será igual a 7^2+7-1=55. Quiere decir que los números no representables respecto al conjunto {8,9} serán no mayores que 55. En efecto, los hemos buscado con hoja de cálculo y resultan ser
1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 19, 20, 21, 22, 23, 28, 29, 30, 31, 37, 38, 39, 46, 47, 55
Su suma es 588, que coincide con PIR6_4(7), como puedes comprobar en la lista de arriba.
Podemos repetir esta comprobación para cualquier otro valor. Para ello necesitamos una función que nos devuelva VERDADERO si un número n es representable respecto al conjunto {a,b}. Puede ser esta:
Function sumamult(n, a, b) As Boolean ‘Investiga si n=t*a+u*t
Dim i, p, q
Dim es As Boolean
es = False
i = 0 ‘Recorrerá los posibles múltiplos de a
While i <= n And Not es
p = i / a: q = (n - i) / b ‘Encuentra los posibles valores de t y u
If p = Int(p) And q = Int(q) Then ‘Si ambos t y u son enteros, es representable
es = True
End If
i = i + 1
Wend
sumamult = es
End Function
Con esta función no es difícil sumar los no representables para un número dado:
Function suma_no_repr(n)
Dim i, s
s = 0
For i = 1 To n * n + n – 1 ‘Busca hasta el número de Frobenius
If Not sumamult(i, n + 1, n + 2) Then s = s + i ‘Si no es representable, lo suma
Next i
suma_no_repr = s
End Function
Efectivamente, con ella se reproduce la lista de los piramidales hexagonales de cuatro dimensiones:
Esto ocurre a menudo en las pequeñas investigaciones matemáticas, que aparecen conexiones inesperadas, como nos ha ocurrido aquí. Era difícil imaginar una conexión de números piramidales con el número de Frobenius.








No hay comentarios:
Publicar un comentario