Potencias equidistantes de cuadrados

En uno de mis cálculos habituales me encontré hace unas semanas con esta igualdad doble:

16124=307^2-5^7
16124=5^7-249^2

Lo interesante de ella es que significa que 5^7 equidista de dos cuadrados, 249^2 y 307^2. Por eso, la función que usaremos más adelante la hemos llamado ENTREDOS, porque investigaremos qué potencias son promedio de dos cuadrados, o, lo que es equivalente, equidistantes de ellos.

Búsqueda ordenada

Para una potencia dada, deberemos recorrer todos los cuadrados inferiores a ella, sumar a la potencia la diferencia entre los dos números, y averiguar si resulta un cuadrado. Por ejemplo, 3125=5^5. Le extraemos la raíz cuadrada entera, y resulta 55. A partir de ese número k, vamos descendiendo valores, elevándolos al cuadrado. Para cada cuadrado k², encontramos la diferencia D=3125-k². Esa diferencia la sumamos a 3125, y deberá resultar un cuadrado entero.

 El esquema podría ser el siguiente: 

Vamos descendiendo valores hasta que la suma sea cuadrada. En la imagen observamos que unas soluciones son 45 y 65. En efecto:

3125-45²=1100 y 65²-3125=1100, luego 5^5 equidista de 45² y 65².

Este proceso es fácilmente automatizable. Lo hemos efectuado en esta función:

Function entredos$(n)
Dim i, r, a, b
Dim s$

s = "" ‘La solución se expresa como texto
If espotencia(n) > 1 Then ‘Es potencia no trivial
r = Int(Sqr(n)) ‘Primer valor a ensayar
i = r - 1
While i > 0 And s = "" ‘Descendemos valores de cuadrados
b = n - i ^ 2 ‘Diferencia entre potencia y cuadrado
a = n + b ‘A la potencia le sumamos la diferencia
If escuad(a) Then b = Sqr(a): s = s + "  " + Str$(i) + " , " + Str$(b)
‘Hemos encontrado una solución
i = i - 1
Wend
End If
entredos = s ‘Si no hay solución, la respuesta está vacía
End Function

La función ESPOTENCIA la hemos publicado en https://hojaynumeros.blogspot.com/2022/04/numeros-consecutivos-con-una-suma-del.html

Estas son las primeras soluciones con potencias no triviales:

Es fácil comprobar cualquiera de ellos, por ejemplo, 125=5^3, potencia no trivial, y se cumple que 125=(9²+13²)/2.

Para poder manejar con comodidad potencias y exponentes grandes, hemos preparado la versión en PARI.

entredos(n)={my(r=truncate(sqrt(n)),i=r-1,a,b,v=0,w=0);if(ispower(n),while(i>0&&v==0&&w==0,b=n-i^2;a=n+b;if(issquare(a),v=i;w=truncate(sqrt(a)));i=i-1));concat(v,w)}
for(i=1,1400,if(entredos(i)<>[0,0],print(i,", ",ispower(i),", ",entredos(i))))

En ella se busca hasta 1400 para que coincida el resultado con la tabla anterior:

Estudio teórico

Las potencias de la tabla no aparecen por casualidad, sino que han de tener una estructura muy determinada. Es especialmente interesante su estudio porque en un principio hemos ignorado las soluciones múltiples para el par de cuadrados, y veremos que se pueden tener previstas si se conoce la descomposición factorial de esas potencias.

Para entender mejor qué suponen estas búsquedas, basta enfocar al doble de esas potencias, porque así el problema es muy tratable. En efecto, si p^k es el promedio entre dos cuadrados, a² y b², significa que 2p^k ha de poderse descomponer en suma de dos cuadrados, y ese problema está resuelto desde Fermat y Gauss. Nos basaremos para nuestro estudio en la fórmula propuesta por Gauss para contar las descomposiciones posibles de un número en dos cuadrados.

Conviene leer nuestra entrada de blog https://hojaynumeros.blogspot.com/2010/10/en-cuantas-sumas-de-cuadrados-2-de-5.html

En ella se comenta la fórmula de Gauss para averiguar en cuántas sumas de cuadrados se puede descomponer un número. Copiamos un párrafo de esa entrada:

“Estas propiedades se resumen en un criterio que no vamos a desarrollar aquí, y es que sólo se pueden descomponer en cuadrados los números en los que los factores primos del tipo 4n+3 figuren en su descomposición con exponente par. Gauss fue más allá en esa sección 182, pues dio una fórmula para contar el número de formas diferentes en las que se descompone un número en suma de dos cuadrados con base no negativa:

donde ES significa “mínimo entero igual o superior” y los factores que le siguen se corresponden con los exponentes de los factores del tipo 4n+1 aumentados en una unidad. La fórmula, como advierte Gauss, sólo es válida si los factores del tipo 4n+3 forman un cuadrado perfecto.”

En este caso, el factor 2 de 2p^k no influye, por lo que el criterio se puede aplicar a la potencia que equidista de dos cuadrados. En efecto, si descomponemos factorialmente esas potencias, obtenemos:

Todas las soluciones poseen factores primos que son, o bien del tipo 4k+1, o el 2, o el tipo 4k+3 elevado a una potencia par, como ocurre en el 900, que hemos destacado en rojo.

Esto nos da un criterio fiable para saber si una potencia no trivial puede equidistar de dos cuadrados.

Vemos un ejemplo:

1368900=170^2, y sus factores primos son 13^2*5^2*3^4*2^2. De ellos, el 3, que es del tipo 4k+3, está elevado a exponente par, los otros, 13 y 5 son del tipo 4k+1, y, finalmente, el 2 no influye. Por eso se sabía con antelación que sería equidistante de dos cuadrados, en este caso son 715716=846^2 y 2022084=1422^2, con la identidad 1368900=(846^2+1422^2)/2.

Soluciones múltiples

Hay que considerar la posibilidad de que una potencia equidiste de más de un par de cuadrados. De hecho, veremos que se dan soluciones múltiples con total seguridad. Para estudiarlas, hemos modificado algo la función ENTREDOS para que nos devuelva, en primer lugar, el número de soluciones. De esa forma, la búsqueda de potencias equidistantes se puede efectuar fijando el número de pares de cuadrados esperados. Hemos organizado una búsqueda para tres pares de soluciones como ejemplo:

Es fácil observar que se cumple la fórmula de Gauss, de emplear la mitad por exceso de los exponentes de los primos tipo 4k+1. En los cuatro ejemplos figura (ha sido algo casual) el factor 5 elevado a 5 o a 6, y no existen factores tipo 4k+3. Tomando la parte entera por exceso de tanto el exponente 5 como del 6 resulta 3, que es el número de pares de cuadrados que hemos conseguido.

Con este criterio seremos capaces de saber el número de pares de cuadrados resultantes sin tener que comprobarlo. Vemos unos ejemplos:

3084588=2^2*3^3*13^4: No debe presentar soluciones, por contener el 3 elevado a potencia impar. En efecto, la función ENTREDOS devuelve un cero:

78125=5^7, luego debe presentar cuatro soluciones, ya que 4 es la mitad por exceso de 7:

Con hoja de cálculo se pueden producir errores de redondeo para números mayores, por lo que es más fiable el razonamiento que la comprobación.

Potencias sucesivas

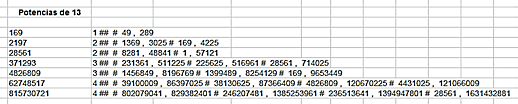
Finalizamos con una curiosidad, y es que, dada una potencia equidistante de dos cuadrados, todas sus potencias presentarán soluciones, que se podrán ir incrementando al aumentar los exponentes de los factores tipo 4k+1. En la imagen podemos estudiar un ejemplo representativo, que recorre las potencias de 13:

El número de soluciones se va repitiendo, por depender de la mitad por exceso, que coincide en dos exponentes consecutivos.