Números consecutivos con una suma del mismo tipo

 

En mis cálculos diarios de Twitter uso a menudo el concepto de suma simétrica, en la que considero tres sumandos con un repetido, y que los tres presenten una misma propiedad. Por ejemplo, 80=2³+4³+2³, es decir, una suma simétrica de cubos. Lo curioso en este caso es que su consecutivo, 81, también presenta esa misma propiedad, ya que 81=3³+3³+3³. ¿Existirán muchos pares de este tipo, que sean consecutivos y con el mismo tipo de suma simétrica?

Como la búsqueda promete ser larga, la dividiremos en tipos. Es ya frecuente en este blog, interrumpir un estudio cuando se perciba que la cuestión se alarga o pierde interés.

Suma simétrica de cubos

Comenzamos por este caso por ser el primero que se consideró. Además del par 80, 81 existen otros, como veremos.

En primer lugar, necesitaremos saber cuándo un número se puede expresar como suma simétrica de cubos. El objetivo inmediato es conocer la forma de identificar un cubo. El problema lo constituyen los decimales y el redondeo, por lo que podemos usar una identificación en dos pasos, extrayendo la raíz cúbica y más tarde comprobar que su cubo coincide con el número deseado. Sería algo así:

Function escubo(n)

Dim a

a = Int(n ^ (1 / 3) + 10 ^ (-6))

If a * a * a = n Then escubo = True Else escubo = False

End Function

 

Un criterio más fiable, pero más lento, es el de extraer los factores primos y exigir que todos los exponentes sean iguales a 3 (o a un múltiplo de 3). Disponemos de una función diseñada para encontrar el exponente común mínimo entre los factores primos de un número natural. Sería esta otra:

Public Function espotencia(n)

Dim i, j, s, p

If n = 1 Then espotencia = 0: Exit Function

p = n

j = sacaprimos(p) ‘Construye la descomposición factorial

s = expo(1)

If j > 1 Then

For i = 2 To j

s = mcd(s, expo(i)) ‘Elige el mínimo MCD de los exponentes

Next i

End If

If s = 1 Then s = 0

espotencia = s

End Function

 

Devuelve el MCD de los exponentes, y si es 3 o múltiplo de 3, ya tenemos un cubo.

En este proceso usaremos la primera versión para encontrar soluciones, y luego verificaremos con la segunda, que es más lenta, sin publicar de nuevo los resultados.

Una vez identificados los cubos, habrá que determinar si un número es suma simétrica de dos cubos. Para eso estaría esta otra función:

Public Function sumasimcubos(n) As Boolean

Dim i, m

Dim novale As Boolean

i = 1

novale = True

While i < (n - 1) ^ (1 / 3) And novale ‘Buscamos el sumando central

If escubo((n - i ^ 3) / 2) Then novale = False ‘Restamos y dividimos entre 2 para ver el otro

i = i + 1

Wend

sumasimcubos = Not novale

End Function

 

Esta función te indica si un número es suma de cubos simétricos o no. Ya solo queda aplicarle esta prueba a dos números consecutivos. En la práctica, la función va a devolver la suma en modo texto, pero no se quería complicar esta explicación. Aplicada de esta forma, nos da los siguientes pares:

Por ejemplo:

176200=44³+18³+44³ y  176201=17³+55³+17³

El lenguaje PARI devuelve resultados con más rapidez, por lo que también es conveniente adaptar a él este proceso. Así llegamos un poco más lejos, pero no se ha pretendido agotar el tema y hemos detenido la búsqueda en 300000

scube(n)={my(i=1,m); while(i<(n-1)^(1/3),m=(n-i^3)/2; if(ispower(m,3),return(1));i+=1)}

ok(n)=scube(n)&&scube(n+1)

for(i=1,300000,if(ok(i),print1(i,", ")))

80, 344, 3429, 7290, 12393, 14749, 61318, 85751, 92609, 95010, 120311, 167399, 170173, 171181, 173743, 173778, 176200, 185442, 250063, 252046, 277694,…

Búsqueda directa con Excel

Podemos organizar una tabla de doble entrada XY en cuyo interior situemos las sumas x³+2y³, y no tendremos más que buscar consecutivos. En la imagen están destacados cuatro pares:

Esto no sería fiable, porque la vista nos puede engañar y perdernos un par. Lo indicado aquí sería escribirlos en columna, ordenarlos después y comprobar que los consecutivos que cumplen la propiedad caen uno debajo del otro.

Este procedimiento sí nos daría más seguridad, pero, o se resolvía con macros, o nos tendría bastante tiempo ocupados. Dejamos esa puerta abierta a nuevos métodos

Suma de  potencias

Después de investigar sobre cubos, lo indicado es pasar a los cuadrados u otras potencias. Con cuadrados aparecen tantos ejemplos que hacen perder el interés por la búsqueda. Si en las funciones usadas para los cubos vamos cambiando los exponentes 3 por 2, obtendremos las sumas simétricas de cuadrados. Los primeros casos de consecutivos son estos:

Llama la atención la aparición de conjuntos de tres consecutivos, como 17, 18, 19, o 66, 67, 68. Como simple curiosidad, se adjuntan a continuación los primeros:

Su misma abundancia le resta interés.

Cuartas potencias

Este caso es mucho menos frecuente. Volvemos a adaptar la función para cubos cambiando 3 por 4 y obtenemos una primera solución:

14802=7⁴+10⁴+7⁴         14803=3⁴+11⁴+3⁴

No existen, al parecer, otras soluciones menores que 10⁶, por lo que dejamos abierta la búsqueda.

Como es nuestra norma, paramos aquí las potencias, para no alargar. Con lo publicado ya hay información suficiente para los lectores que deseen emprender otras búsquedas.

Otros tipos

Al comenzar a redactar esta entrada parecía que existiría gran variedad de soluciones en otros tipos de números, pero la realidad nos ha devuelto casos con demasiados resultados o con demasiado pocos. Esto hace perder interés a lo que sigue, pero hemos preferido mantenerlo.

Triangulares

Este tipo de números lo consideramos muy a menudo en nuestras búsquedas, porque no suele defraudar. Habrá que alterar ligeramente nuestra función, pues usaremos ESTRIANGULAR, que puedes encontrar en muchas entradas de este blog. Quedaría la función así (la seguimos llamando sumasimcubos):

Public Function sumasimcubos$(n)

Dim i, m, p, q

Dim s$

i = 1

s = ""

While i < Sqr(2 * n) And s = "" ‘El mayor triangular sería Sqr(2*n)

q = i * (i + 1) / 2 ‘Se construye el primer triangular

m = (n - q) / 2 ‘Diferencia para encontrar los simétricos

If estriangular(m) And m > 0 Then  s = Str$(m) + ", " + Str$(q) + ", " + Str$(m) ‘Es triangular y paramos

i = i + 1

Wend

sumasimcubos = s

End Function

Con esta función se obtienen muchas soluciones, como nos ocurrió con los cuadrados:

No tiene interés seguir.

Oblongos

Es inútil buscarlos, porque todos son pares y no puede darse la propiedad buscada en dos números consecutivos, uno par y otro impar.

Primos

Para que se cumpla lo que pretendemos, en uno de los consecutivos el primo central deberá ser 2, pero no tendremos esto en cuenta y sustituiremos triangular por primo y estriangular por esprimo. Como no existe fórmula para los primos, usaremos la función para el próximo primo PRIMPROX. Todas ellas ya han sido usadas en otras entradas.

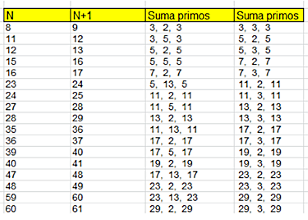
Al ser obligada la presencia del 2 en uno de los números hace que aparezcan muchos consecutivos en los que el término central es 2 en el menor y 3 en el mayor, como puede comprobarse en este resultado:

También aquí obtenemos muchos resultados. Nos estamos quedando con pocos tipos interesantes. Hemos intentado con los números de Fibonacci y también resultan muchas soluciones, demasiadas para sacar consecuencias interesantes. Con los factoriales también se desvirtúa la búsqueda con 1! y 2! que son consecutivos. Así que hasta aquí llegó el estudio.