En esta entrada y la siguiente vamos a trabajar un poco con las sumas de los primeros primos, y ampliaremos a alguna potencia. La idea es encontrar curiosidades o propiedades, así como la naturaleza de esas sumas.
Herramientas
previas con Excel y Calc
Comenzamos con una función que sume potencias de los
primeros primos:
Public Function sumprimoene(a, k) As
Long
Dim prim, n, s As Long
prim = 2 ‘Primer primo
n = 1 ‘Contador
s = 2^k ‘Primera
suma
While n < a
prim = primprox(prim) ‘A
cada primo le encontramos el siguiente
n = n + 1 ’Se
incrementa el contador
s = s + prim ^ k ‘Sumamos
la potencia del primo
Wend
sumprimoene = s
End Function
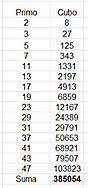
Por ejemplo, con esta función obtenemos la suma de los cubos de los primeros 15 primos:
SUMPRIMOENE(15;3)=385054
Podemos comprobarlo con esta tabla:
Versión PARI
La función básica en PARI es similar. Hemos usado la
siguiente función IS en los valores 15 (número de primos) y 3 (exponente):
is(a,k)={my(s=2^k,n=1,p=2);while(n<a,p=nextprime(p+1);n+=1;s=s+p^k);s}
print(is(15,3))
En la web de PARI/GP hemos introducido este código para
comprobar el resultado
Versión
elemental con el Buscador
Nuestro Buscador de Naturales (http://www.hojamat.es/sindecimales/divisibilidad/herramientas/herrdiv.htm#buscador)
suma primos, y veremos en la siguiente entrada que también puede sumar
potencias. Basta escribir la condición PRIMO y la de EVALUAR TOTALES. En la
imagen figuran los primeros primos y sus sumas parciales:
El resultado es 160.
Suma
de primos igual a un primo
La suma de los primeros primos puede ser también un
número primo. El primer caso elemental, además del mismo 2, es el 2+3=5, y el
siguiente, 2+3+5+7=17
Con la función ya explicada en VBA de Excel se puede
establecer una búsqueda sencilla de primos que son suma de los primeros primos.
El resultado es:
A013918 Primes equal to the sum of the
first k primes for some k.
2,
5, 17, 41, 197, 281, 7699, 8893, 22039, 24133, 25237, 28697, 32353, 37561,
38921, 43201, 44683, 55837, 61027, 66463, 70241, 86453, 102001, 109147, 116533,
119069, 121631, 129419, 132059,
Nos vale en PARI el procedimiento publicado por Michael
B. Porter en esa página:
n=0;
forprime(k=2, 2300, n=n+k; if(isprime(n), print(n)))
Aquí aprovecha que forprime recorre los primos rápidamente.
Procedimiento
con el Buscador
El carácter elemental de esta herramienta no permite
bucles como los usados hasta ahora, pero una instrucción reciente nos permite
visualizar los mismos resultados:
Resalta en la lista los totales que son primos.
Otros
resultados
La suma puedes ser un cuadrado, aunque no abundan los resultados.
Cuadrados
Procedimientos similares a los anteriores nos dan hasta
seis soluciones. Por ejemplo, con PARI usamos
n=0;
forprime(k=2, 2*10^6, n=n+k; if(issquare(n), print1(n,", ")))
Obtenemos cuatro fácilmente:
100, 25633969, 212372329, 292341604, 3672424151449,
219704732167875184222756
Como estamos comparando números de naturaleza distinta,
no es fácil descubrir propiedades.
Triangulares
Para saber si un número T es triangular basta con exigir
que 8*T+1 sea cuadrado. Corregimos el código PARI y queda:
n=0; forprime(k=2, 2*10^6, n=n+k; if(issquare(8*n+1), print1(n,", ")))
Lo ejecutamos en la web de PARI:
A066527 Triangular numbers that for some k
are also the sum of the first k primes.
10,
28, 133386, 4218060, 54047322253, 14756071005948636, 600605016143706003,
41181981873797476176, 240580227206205322973571, 1350027226921161196478736
Otros
ejemplos
De números oblongos
solo hemos encontrado el 2 entre los menores de 2*10^7. De cubos, ninguno. De la sucesión de Fibonacci, tres: 2, 5 y 2584
(entre los menores de 7*10^7)
Es normal que no se encuentren muchos.







No hay comentarios:
Publicar un comentario