Primeras definiciones y propiedades
Incluimos aquí el estudio de los números cuadrados,
considerándolos prioritariamente como números poligonales, y dejando como
complementarias las cuestiones derivadas de su naturaleza como producto n*n.
Cuadrado
como n*n
La primera idea que se tiene de los números cuadrados es
que son el resultado de multiplicar un número entero por sí mismo: C=n*n (por
eso, a la operación n2 se le ha dado el nombre de elevar al cuadrado).
Se les llama también cuadrados perfectos. Este producto
se puede representar como una matriz cuadrada de puntos.
Es conveniente disponer de un criterio para saber si un
número es cuadrado. El más fiable es el de descomponer el número en factores primos
y observar si todos los exponentes son pares. Esto es así porque si un número
primo p divide a un cuadrado, p2 también lo divide.
Así se evitan los decimales que aparecen en otros
criterios. El inconveniente radica en la programación de la extracción de
factores. En el otro extremo de la definición encontramos los números libres de cuadrados, en los que
todos los exponentes son impares.
Un criterio menos fiable es el de sacar la raíz cuadrada,
tomar su redondeo a un número natural o su parte entera (llamada raíz cuadrada
entera) y ver si al elevarla al cuadrado reconstruye el número inicial. Así se
procede en esta función:
Public Function escuad(n) As Boolean
If n < 0 Then
escuad = False
Else
If n = Int(Sqr(n)) ^ 2 Then escuad = True
Else escuad = False
End If
End Function
En lenguajes avanzados de programación se dispone ya de una función issquare o similar.
Esta definición permite considerar que un número cuadrado
puede terminar solo con las cifras 0, 1, 4, 5, 6 o 9 en el sistema de
numeración decimal. Es fácil comprobarlo multiplicando números por sí mismos.
Así que un número que termine en 2, 3, 7, 8 no será cuadrado.
Esta definición de cuadrado también nos lleva a que tendrá un número impar de divisores.
Si todos los exponentes de factores primos son pares, el número de divisores
será un producto de impares, y por tanto impar. Puedes revisar esta idea en
nuestro documento http://www.hojamat.es/sindecimales/divisibilidad/teoria/teordivi.pdf
Aquí tienes un volcado del párrafo en el que se
desarrolla la fórmula correspondiente:
Este sería un buen criterio para detectar si un número es cuadrado, pero resulta largo y lento.
Cuadrado
como número poligonal
La construcción de un cuadrado siguiendo los
procedimientos generales de construcción de poligonales nos llevaría a un
esquema como el de la imagen:
En ella observamos sin dificultad que el número cuadrado
n2 es la suma de los primeros números impares: 1+3+5+7+9=25=52
El caso general se demuestra por inducción completa:
Si n2 equivale a la suma
(2*0+1)+(2*1+1)+(2*2+1)+(2*3+1)+…+(2*(n-1)+1),
el siguiente cuadrado, (n+1)2 es igual a n2+(2*n+1),
lo que completa la suma de impares.
Así que se cumple
Sumas de números impares consecutivos
Una consecuencia de esta propiedad es la de que cualquier
suma de números impares consecutivos equivale a la diferencia entre dos
cuadrados. Por ejemplo, la suma 55+57+59+…+87+89+91 se puede calcular como la
diferencia entre estas dos sumas:
(1+3+5+7+…+91)-(1+3+5+7+53)=46^2-27^2
El 46 y el 27 se obtienen teniendo en cuenta, según la
fórmula anterior, que los sumandos tienen la forma 2k+1.
Si se toman dos sumandos impares consecutivos, el
resultado será un cuadrado par 2n*2n=4n2, pues
Si multiplicamos dos números pares (o impares) consecutivos y añadimos una unidad obtenemos también un cuadrado, pues n(n+2)+1=n2+2n+1=(n+1)2
Cuadrado
como suma de dos triangulares
Otra generación de cuadrados viene dada, tal como vimos
en el tema correspondiente, como suma de dos triangulares consecutivos. En la
imagen se observa que el cuadrado 25 es la suma de los triangulares 10 y 15.
Como un triangular es un número combinatorio, esta propiedad se puede expresar como (elegimos el símbolo C(n) para representar el cuadrado de orden n):
Desde el punto de vista de los cuadrados esta relación no tiene más interés.
Cuadrado
como suma de OBLONGO(N)+N+1
Otra relación que se queda en simple curiosidad es que si
a un oblongo le añadimos su lado mayor, se convierte en un cuadrado.
En efecto, los oblongos vienen dados por la expresión
n(n+1), y si le sumamos n+1 se convierte en n(n+1)+(n+1)=(n+1)(n+1)=(n+1)2
Esta
propiedad es más sugestiva si se expresa al revés: si a un conjunto cuadrado le
eliminas un lado, se convierte en oblongo.
Si al cuadrado 64 le quitamos un lado (8) nos queda 56,
que es oblongo, por ser 7*8.
Una curiosidad
Copiamos un texto publicado por Amarnath Murthy, Mar 24
2004en la página de OEIS:
Begin
with n, add the next number, subtract the previous number and so on ending with
subtracting a 1: a(n) = n + (n+1) - (n-1) + (n+2) - (n-2) + (n+3) - (n-3) + ...
+ (2n-1) - 1 = n^2.
Como invitación a demostrarlo, insertamos ese proceso
aplicado al número 12:
En la primera columna se sitúan los números consecutivos a 12 y en la segunda los anteriores. Se suman y se restan unos de otros, resultando al final 144=122.



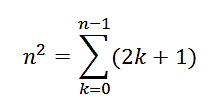




No hay comentarios:
Publicar un comentario