Pedro D. Pajares (@Pedrodanielpg) twitteó el día 31/12/21
En
Matemáticas decimos que un número es ADMIRABLE si al SUMAR sus divisores
propios (todos los divisores salvo él mismo) CAMBIANDO EL SIGNO de uno de
ellos, obtenemos el mismo número.
(https://twitter.com/Pedrodanielpg/status/1476932068827443203?t=uj-WEOnFugC2oAdYEfpnWw&s=03)
Como ya es tradicional en
este blog, Twitter nos proporciona detalles que se pueden extender en varias
direcciones. Es lo que efectuaremos con los números admirables. Hay que
agradecer a Pedro D. Pajares su información.
No sigo con atención los
nombres algo curiosos que se suelen dar a números naturales, por lo que no
conocía este término de “admirable”. Imagino que se lo merecen números que,
como veremos, presentan una cercanía teórica con los números perfectos. En
estos la coincidencia se da con la suma de todos los divisores propios (parte
alícuota) y en los admirables a esa suma hay que restarle el doble de uno de
los divisores, para que así cambie su signo en la suma.
Por ejemplo, es admirable
650, porque sus divisores propios suman de esta forma:
652=325+130+65+50+26+25+13+10+5+2+1
La diferencia entre 650 y la
suma de los divisores propios es 2, luego bastará cambiar de signo al 1:
650=325+130+65+50+26+25+13+10+5+2-1
Este sencillo cálculo nos da
una pista de cómo saber si un número es admirable:
- Ha de ser abundante, es decir, que la suma de
sus divisores propios sea mayor que él
- La diferencia entre ambos ha de ser par, y su
mitad, divisor del número.
Con estas condiciones es
fácil saber si un número es abundante o no. Como es costumbre, comenzaremos con
una búsqueda de “fuerza bruta” y después la mejoraremos.
En cualquier método que
usemos, habrá que usar la función SIGMA, que está implementada en muchas
herramientas. No lo está en hojas de cálculo, pero si buscas “Sigma”, o
“función sigma” en este blog encontrarás nuestra versión. Por ejemplo, en https://hojaynumeros.blogspot.com/2019/10/la-funcion-sigma-y-sus-traslados.html
Con esta función es
fácil construir que nos indique si un número es admirable:
Public Function
esadmirable(a)
Dim s, i, d
'Es suma de sus
divisores propios cambiando a uno de signo
s = sigma(a) - a 'Partes alicuotas
d = 0
i = 1
While i <= a / 2 And d =
0 ‘Recorre divisores
If a / i = a \ i Then
If s - 2 * i = a Then d = i ‘Si
es divisor y construye la suma adecuada, es la solución
End If
i = i + 1
Wend
esadmirable = d ‘Devuelve
un 0 si no encuentra el divisor adecuado.
End Function
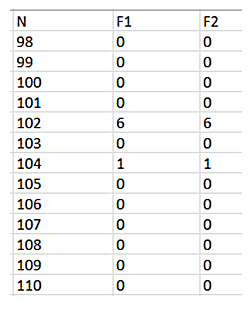
Con esta función distinguimos los admirables de los que no lo son. En estos últimos devolvería un cero. En este intervalo elegido al azar, aparecen dos admirables:
Son el 102, con divisor 6 y
104 con el 1. En efecto:
102=51+34+17-6+3+2+1
104=52+26+13+8+4+2-1
Esta función es ineficiente.
Con las ideas expresadas más arriba, es mejor esta:
Public Function
esadmirable(a)
Dim s, i, d, es
'Es suma de sus divisores propios cambiando a uno de signo
s = fsigma(a, 1) - a 'partes alicuotas
d = s – a ‘Halla
la diferencia entre la suma de divisores propios y el número
If d > 0 And d / 2 = d \
2 Then ‘La diferencia ha de ser positiva y par
i = d / 2 ‘Si
la mitad de la diferencia es un divisor, es un número admirable
If a / i = a \ i Then es = i
Else es = 0
End If
esadmirable = es
End Function
Si volvemos al intervalo elegido en párrafos anteriores se puede comprobar la equivalencia entre ambas funciones:
Según las condiciones de
este planteamiento, existirán infinitos números admirables, porque lo serán
todos los múltiplos de 6 formados como 6p, con p primo mayor que 3. En efecto:
Si N=6p, con primo y mayor
que 3 (para eliminar los casos 2 y 3), sus divisores serán 1, 2, 3, 6, p, 2p,
3p, 6p y la suma de los divisores propios (eliminando 6p) tendrá el valor de
12+6p, con lo que su diferencia con N será 12, que cumple la condición de ser
par y doble de un divisor. Por tanto, en estos números el divisor que hay que
cambiar de signo es el 6, como vemos en esta tabla de múltiplos de 6 de este
tipo:
(29691198404, 29691198405) y
(478012798575, 478012798576).
Sabemos que todos los admirables son abundantes, pero se puede concretar afirmando que su abundancia (cociente entre SIGMA(N) y N) está entre 2 y 3
(https://hojaynumeros.blogspot.com/2011/05/como-crece-la-abundancia.html)
En efecto, por ser
abundante, ha de ser mayor que 2, pero si fuera superior a 3, la diferencia con
las partes alícuotas no podría ser el doble de un divisor. Lo vemos en los
múltiplos de 6 que hemos estudiado:
Números
compatibles
Al igual que los números
perfectos dan lugar a los números amigos, como aquellos en los que cada uno de
ellos coincide con la suma de divisores propios del otro (Números amigos - Wikipedia, la enciclopedia libre),
los admirables dan lugar a los compatibles.
En un par de números
compatibles, cada uno de ellos coincide con la suma de los divisores propios
del otro si en esa suma se ha cambiado de signo un divisor.
Por ejemplo, 24 Y 28 son
compatibles, según estas dos sumas:
28=12+8+6-4+3+2+1 (divisores
propios de 24)
24 =14+7+4-2+1
(ídem de 28)
Los números menores de cada
par están publicados en A109797 - OEIS:
24, 30, 40, 42, 48, 60, 80,
80, 96, 102, 126, 140, 140, 156, 156, 156, 174, 180, 180, 198,…
Los mayores de cada par se
encuentran en http://oeis.org/A109798, y
son:
28, 40, 42, 52, 60, 96, 102,
104, 124, 110, 182, 182, 188, 210, 230, 234, 184, 358, 362,…
Las repeticiones en ambas
listas son una prueba de que esta relación no es biunívoca.
Hemos diseñado una función
de dos variables para Excel, que nos devuelve el factor de cada una para que
los números sean compatibles:
Public Function
soncompatibles$(a, b)
Dim s, i, d
Dim s1$, s2$
s = fsigma(b, 1) - b 'partes alicuotas de b
d = 0
i = 1
ss$ = ""
While i <= b / 2 And d =
0
If b / i = b \ i Then
If s - 2 * i = a Then d = i:
s1$ = "De b: " + Str$(d)
End If
i = i + 1
Wend
If s1 <> ""
Then
s = fsigma(a, 1) - a 'partes
alicuotas de a
d = 0
i = 1
While i <= a / 2 And d =
0
If a / i = a \ i Then
If s - 2 * i = b Then d = i:
s2$ = " De a:" + Str$(d)
End If
i = i + 1
Wend
End If
If s1 <> ""
And s2 <> "" Then ss = s1 + s2 Else ss = "NO"
soncompatibles = ss
End Function
No necesita explicación, porque es como una duplicación de la función para admirables. Si los números no son compatibles devuelve un NO. Con esta función y una búsqueda adecuada se pueden descubrir compatibles mayores que los publicados.
Por ejemplo, con esta función mayorcompatible es posible encontrar los mayores compatibles que figuran entre 1000 y 1100:
Public Function mayorcompatible(b)
Dim i
Dim a$, c$
i = 2
a = ""
While i < b And a =
""
c$ = soncompatibles(i, b)
If c$ <> ""
Then a$ = c$ + " con " + Str$(i)
i = i + 1
Wend
If a$ = "" Then a$
= "NO"
mayorcompatible = a$
End Function
El resultado es:
1012 De b: 1 De a: 1 con 1002
1016 De b: 4
De a: 64 con 896
1022 De b: 2
De a: 50 con 750
1026 De b: 342
De a: 6 con 690
1034 De b: 2
De a: 2 con 690
1050 De b: 525
De a: 73 con 876
Hay que interpretar que, en primer lugar, figuran los divisores que hay que cambiar de signo, y en segundo lugar, el otro número del par de compatibles. Así el 1022 es compatible con 750 si cambiamos de signo el factor 2 de 1022 y el 50 de 750. Así:
750=511+146+73+14+7-2+1
1022 =375+250+150+125+75-50+30+25+15+10+6+5+3+2+1
El encontrar el menor compatible es más complejo, porque de entrada no se puede saber hasta dónde buscar. Se puede adaptar la anterior función a una cota, por ejemplo a tres veces el número, sabiendo que sólo es válido el resultado positivo, si completa el par, pero ante resultados negativos habría que subir esa cota.



No hay comentarios:
Publicar un comentario