Si manejamos muchos tipos de números, observaremos que no es infrecuente que un número de un tipo sea suma de otros dos que comparten ese tipo con él. Los ejemplos más sencillos son los números pares, en los que es fácil descomponer un par en suma de otros dos (incluido el 0), como 22=10+12. También es clásico el ejemplo de las ternas pitagóricas, en las que un cuadrado (de la hipotenusa) es suma de otros dos cuadrados (los de los catetos), como 5^2=3^2+4^2. El caso más conocido es el de los números de Fibonacci, que son suma de los dos anteriores.
Según el Último Teorema de Fermat, no podemos buscar otros
ejemplos con cubos o potencias mayores, así que no trataremos con potencias.
(https://es.wikipedia.org/wiki/%C3%9Altimo_teorema_de_Fermat)
En este blog solemos manejar frecuentemente números
semiprimos, oblongos, triangulares y poligonales. De los primos no hablamos,
porque solo cumplirían esto los términos mayores de un par de primos gemelos,
como 19=17+2
Realizaremos unas búsquedas y razonamientos sobre algunos de ellos.
Suma de
semiprimos
Llamamos semiprimos a los números que son producto de dos
factores primos, iguales o diferentes.
Para identificar semiprimos usamos esta función de Excel
(creada en este blog)
Public Function essemiprimo(n) As Boolean
Dim a, b, r
Dim es As Boolean
es = False ‘Al principio suponemos que no es semiprimo
a = 2 ‘La variable a recorrerá los números primos
r = Sqr(n)
While a <= r And Not es
b = n / a ‘Dividimos n entre el primo y si el
cociente es primo, ya lo tenemos
If esprimo(b) Then es = True
a = primprox(a) ‘Se busca el próximo primo
Wend
essemiprimo = es
End Function
Hemos tenido que crear esta función porque el lenguaje VBasic es algo pobre para estos cálculos. En PARI lo tendríamos más fácil. Basta pedir que bigomega(n)=2. Esta función cuenta factores primos con repetición. Si vale 2, es que n es semiprimo.
Tanto con una como con la otra, tomaremos semiprimos, los
descompondremos en dos sumandos y si ambos también son semiprimos, habremos encontrado un ejemplo.
En Excel usamos la función SUMATIPO que está diseñada para
adaptarla a todos los casos que estudiemos en esta entrada. En el listado
figura la búsqueda de semiprimos:
Function sumatipo$(n)
Dim i, j
Dim s$
s = ""
If essemiprimo(n) Then
i = 4 ‘Primer semiprimo
While i < n And s = ""
If essemiprimo(i) Then
j = n - i
If essemiprimo(j) Then s = Str$(i) + Str$(j) ‘Da la
solución si la encuentra
End If
i = i + 1
Wend
End If
sumatipo = s ‘Devolverá un texto con la
solución
End Function
Esta función devuelve una cadena vacía si no cumple la
condición o los dos sumandos si la cumple.
Si organizamos una búsqueda obtendremos el resultado
inesperado de que todos los semiprimos se descomponen así salvo cinco (4, 6, 9,
22 y 33 http://oeis.org/A137253)
En efecto, los primeros a partir del 10 se
descomponen así:
10=2*5=6+4=2*3+2*2
14=2*7=10+4=2*5+2*2
15=3*5=6+9=2*3+3*3
Puedes reproducir la búsqueda con PARI. Inserta en la
página https://pari.math.u-bordeaux.fr/gp.html el
siguiente código:
sumatipo(n)=my(m=0);if(bigomega(n)==2,i=4;while(m==0&&i<n,if(bigomega(i)==2&&bigomega(n-i)==2,m=1);i+=1));m
for(i=6,200, if(sumatipo(i),print1(i,",
")))
Obtendrás todos los semiprimos salvo 4, 6, 9, 22
y 33:
Si sustituimos sumatipo(i) por bigomega(i)==2&&sumatipo(i)==0 y comenzamos en el 4, obtendremos
Son las cinco excepciones.
En los ejemplos de más arriba, los sumandos semiprimos
comparten algún factor. Casi todos los semiprimos se pueden descomponer en
sumandos con los cuatro factores distintos, como por ejemplo 95, que se
descompone como 21+74=3*7+2*37, y los cuatro factores primos 3, 7, 2 y 37 son
todos distintos.
Hay una forma de encontrarlos con PARI:
sumatipo(n)=my(m=0);if(bigomega(n)==2,i=4;while(m==0&&i<n,if(omega(i)==2&&omega(n-i)==2&&omega(i*(n-i))==4,m=1);i+=1));m
for(i=4,250, if(sumatipo(i),print1(i,", ")))
En esta función sumatipo
usamos omega para exigir que los sumandos sean semiprimos y su producto
tenga cuatro factores primos, lo que garantiza que sean los cuatro distintos.
Al aplicarla nos llevamos la sorpresa de que todos los
semiprimos a partir de 85 pueden descomponerse de esa forma. Los semiprimos que
no lo admiten son
4, 6, 9, 10, 14, 15, 21, 22, 25, 26, 33, 34, 35, 38, 39, 46,
51, 58, 62, 82.
Es solo una conjetura.
Suma de
triangulares
Si en la función sumatipo
sustituimos essemiprimo por estriangular, podremos encontrar los
números triangulares (tipo N(N+1)/2) que se descomponen en suma de otros dos
triangulares. La función estriangular
se basa en que si n es triangular, 8n+1 es cuadrado (ver https://hojaynumeros.blogspot.com/2009/12/suma-de-tres-numeros-triangulares.html)
Basándonos en esa propiedad, la función puede tener este
código:
Public function estriangular(n) as boolean
dim a
a = Int(sqr(8*n+1))
if a*a=8*n+1 then estriangular = true else
estriangular = false
end function
Hecha la sustitución obtenemos los triangulares que son suma
de otros del mismo tipo:
6, 21, 36, 55, 66, 91, 120, 136, 171, 210, 231, 276, 351,
378, 406, 496, 561, 666, 703, 741, 820, 861, 946, 990, 1035, 1081, 1176, 1225,
1326, 1378, 1431, 1485, 1540, 1596, 1653, 1711, 1770, 1891, 1953, 2016, …
Están publicados en http://oeis.org/A089982
Por ejemplo, 1326=465+861, y los tres son triangulares
Cuando un número m
es suma de dos triangulares se cumple que todos
los factores primos de 4m+1 son del tipo 4k+1, porque ese número es suma de
dos cuadrados al menos. En efecto, se puede plantear:
Esto equivale a
Es decir
Para que un número admita esta descomposición ningún factor primo suyo puede ser del tipo 4k+3, luego 8m+2 lo cumplirá, y también su mitad 4m+1, ya que el 2 no influye en esa posibilidad.
Por otra parte, en los números triangulares la expresión 8m+1
es un cuadrado, luego 8m+2 es igual a otra suma de cuadrados distinta de la
anterior, y sus factores primos del tipo 4k+1 serán al menos dos, e igual le
ocurrirá a su mitad 4m+1.
Lo vemos con un ejemplo: 21 es un triangular que se
descompone en suma de dos triangulares, ya que 21=15+6, es decir, que
6*7/2=5*6/2+3*4/2, y el valor de 4m+1 es en este caso 85, que se descompone
como 85=5*17=(4*1+1)(4*4+1), luego ambos factores primos son del tipo 4k+1 y
son dos, con lo que se cumple la consideración indicada en el párrafo anterior.
Además, 85=72+62.
Esta búsqueda es similar a la anterior, con la sustitución de
la expresión 8m+1 (que es un cuadrado en los triangulares) por 4m+1, que tiene
una propiedad similar en los oblongos. Corregimos la función sumatipo en este sentido y obtenemos los
números oblongos que son suma de dos oblongos:
12, 42, 72, 110, 132, 182, 240, 272, 342, 420, 462, 552, 702,
756, 812, 992, 1122, 1332, 1406, 1482, 1640, 1722, 1892, 1980, 2070, 2162,
2352, 2450, 12, 42, 72, 110, 132, 182, 240, 272, 342, 420, 462, 552, 702, 756,
812, 992, …
Por ejemplo, 462 es oblongo, ya que 462=21*22, y se
descompone en 462=42+420, que son ambos oblongos: 42=6*7 y 420=20*21
Este listado lo hemos obtenido con la versión en PARI, que es
más rápida.
sumatipo(n)=my(m=0);if(issquare(4*n+1),i=2;while(m==0&&i<n,if(issquare(4*i+1)&&issquare(4*(n-i)+1),m=1);i+=1));m
for(i=4,5000, if(sumatipo(i),print1(i,", ")))
Estos números poseen una propiedad similar a la de los
triangulares, y es que si m es uno de ellos, 2m+1 solo tiene factores primos
del tipo 4k+1 y al menos dos.
Por ejemplo, 72 es oblongo (8*9) y suma de oblongos, 42 (6*7)
y 30 (5*6), y en este caso 2*72+1=145 tiene como factores primos 5 y 29, ambos
del tipo 4k+1.
Sus índices, aunque con otra orientación, están
publicados en http://oeis.org/A012132
Otros
poligonales
Hemos estudiado los números triangulares y no hemos
considerado los cuadrados porque este caso es propio de las ternas pitagóricas
(https://es.wikipedia.org/wiki/Terna_pitag%C3%B3rica).
Pasamos entonces a los números pentagonales, ya estudiados
este año aquí.
https://hojaynumeros.blogspot.com/2020/11/numeros-pentagonales-1.html
https://hojaynumeros.blogspot.com/2020/11/numeros-pentagonales-2.html
Si lees estas entradas comprobarás que el criterio para ver
si un número P es pentagonal consiste en que ha de ser cuadrado 1+24P. Si en la
función sumatipo uso la función
explicada en ellas ordenpentagonal,
basta pedir que no sea nula para que aparezcan los primeros casos.
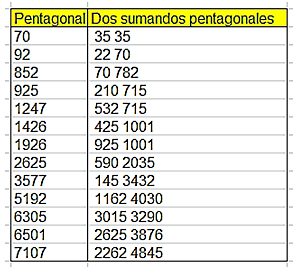
Son estos:
Estos números están publicados en http://oeis.org/A136117
Números
hexagonales
Se tratan igual que los pentagonales, siguiendo las funciones
definidas en las entradas de este blog dedicadas a ellos.
El resultado es
Publicados en http://oeis.org/A133215
Aquí paramos el estudio.






No hay comentarios:
Publicar un comentario