Después de estudiar la formación de los números hexagonales desde varios aspectos en la anterior entrada, es el momento de pasar a sus propiedades. Sólo se incluyen algunas seleccionadas, las más adecuadas para el nivel que desea tener esta entrada.
Otras
propiedades
Los
números hexagonales son el resultado de sumar los números del tipo 4k+1 a
partir del 1.
En efecto:
H1=1, H2=1+5=6, H3=1+5+9=15,…
En general, aplicando la fórmula para sumar progresiones aritméticas:
Los números
hexagonales coinciden con el semiperímetro en las ternas pitagóricas primitivas
en las que la hipotenusa es consecutiva con el cateto mayor.
(Ver http://oeis.org/A000384, comentario
de Lekraj Beedassy)
En efecto, estas ternas se pueden representar como
(m2-n2, 2mn, m2+n2,).
El primer lado y la hipotenusa no pueden ser consecutivos, pues su
diferencia es al menos de dos unidades, luego si los hay son los dos últimos:
Si m2+n2-2mn=1, será (m-n)2=1 y m-n=1,
n=m-1, porque n<m.
El perímetro es 2m(m+n) y el semiperímetro m(m+n)=m(2m-1), que es un
número hexagonal.
Por ejemplo, en la terna (9, 40, 41) son consecutivos 40 y 41, el
perímetro vale 90 y su mitad, 45, es un número hexagonal.
Descomposición
en suma de cuatro hexagonales
Salvo unos pocos números (5, 10, 11, 20, 25, 26, 38, 39, 54, 65, 70, 114
y 130. Ver https://oeis.org/A007527), todos
los demás se pueden expresar como suma de cuatro números hexagonales.
Lo comprobamos con nuestra herramienta Cartesius para el intervalo
(100,110):
Incluimos el planteo. Aunque no hayas manejado esta herramienta lo
entenderás:
xvar=100&110 ‘Recorremos
desde 100 a 110
xtotal=4 ‘Son
cuatro los sumandos
xt=1..9 ‘Cada sumando actúa sobre
el intervalo (1,9)
xt=suc((n-1)*(2*n-3)) ‘Número
hexagonal n-1 (para abarcar el cero)
suma=vx ‘La suma también va del 100
al 110
creciente ‘Para
evitar repeticiones
Según MathWorld, Legendre demostró que todo número mayor que 1791 es una
suma de cuatro números hexagonales, y Duke y Schulze-Pillot mejoraron esto a
tres números hexagonales por cada entero suficientemente grande (https://mathworld.wolfram.com/HexagonalNumber.html)
Un número
hexagonal equivale a la suma de un triangular con el mismo índice sumado con el
triple del triangular anterior.
Es decir: Hxn=Tn+3Tn-1
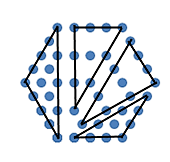
Dejamos como ejercicio la demostración algebraica, porque la imagen
siguiente es bastante clarificadora. El primer triángulo tiene índice 5 y los
otros tres, 4.
Hxn=n+4Tn-1
También es fácil de demostrar algebraicamente.
Los
números hexagonales son permutaciones con repetición de 2n elementos {0,1} en las que el 1 figure repetido dos
veces.
Lo que estamos afirmando es la validez de esta fórmula (permutaciones
con repetición o número binomial):
http://www.hojamat.es/sindecimales/combinatoria/herramientas/herrcomb.htm#combimaq
Hemos usado estas condiciones:
Es fácil su demostración algebraica:
La suma de
los inversos de los números hexagonales equivale al doble del logaritmo
neperiano de 2 (Vaclav Kotesovec, Apr 27 2016)
Finalizamos este recorrido por las propiedades de los números
hexagonales aproximando la suma de sus inversos mediante hoja de cálculo. Se
puede comprobar creando una columna con los números hexagonales, adosando junto
a ella una columna de inversos y usando después la suma. Si deseas avanzar a
miles de términos, es preferible la siguiente función:
Public Function sum_inv_hex(n)
Dim i, s
s = 0
For i = 1 To n
s = s + 1 / (i * (2 * i - 1))
Next i
sum_inv_hex = s
End Function
Su código se entiende fácilmente. Te puedes crear un esquema en el que
escribas el número de términos y le apliques la función para comparar el
resultado con 2LOG(2):
Una forma sencilla para comprobar esto se basa en nuestra hoja de
cálculo “Visor de sucesiones”
(http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#visor)
Le escribimos la fórmula del inverso de un número hexagonal
Activamos el Visor y nos devuelve una aproximación a la suma:
Con esto finalizamos el tema.
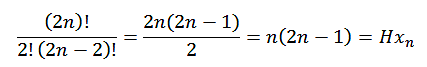
No hay comentarios:
Publicar un comentario