En la entrada anterior de esta serie (http://hojaynumeros.blogspot.com.es/2017/06/cartesius-5-particiones-1.html) procedimos a crear particiones en un número, y en algunas condicionamos los sumandos, para que fueran primos, triangulares o cuadrados. Ahora condicionaremos los resultados, y más adelante repasaremos los condicionamientos clásicos.
Condicionamientos sobre resultados
Las particiones de un número las hemos definido a partir de todas las sumas posibles, pero estas podrían ser condicionadas, en el sentido de suprimir algunas de ellas. Lo vemos con un ejemplo:
¿De cuántas formas podemos descomponer el número 7 en particiones con los dos sumandos menores iguales?
Si no condicionamos los sumandos, existen, según vimos, 15 particiones. Al obligar a que los dos menores sean iguales, restringiremos ese número. Podemos plantearlo así:
XRANGO=7
XT=1..7
CRECIENTE
ES X1=X2
SUMA=7
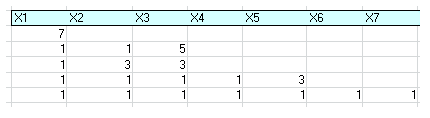
Es el mismo planteamiento de la entrada anterior sobre el tema de particiones, con el añadido ES X1=X2, que obliga a que los dos primeros sumandos sean iguales. Como hemos decidido que los arreglos sean crecientes, estos dos primeros serán también los menores. El resultado es:
Resultan ocho particiones en lugar de 15.
Podemos introducir muchos más condicionamientos: fijar la suma parcial de los tres menores o exigir que el tercer sumando sea mayor que el segundo, y otros parecidos.
Particiones condicionadas
Todos estos condicionamientos se suelen expresar como función así:
P(N/condicionamiento)
De esta forma, el anterior ejemplo se escribiría como P(7/x1=x2)
Otro ejemplo
Imaginemos que deseamos que el tercer sumando sea a su vez suma de los dos anteriores. Procederíamos así:
XRANGO=7
XT=1..7
CRECIENTE
ES X3=X1+X2
SUMA=7
Al desarrollar veríamos que es un ejemplo sin interés, porque sólo existe una suma así (siendo sumandos crecientes)
En efecto, si los valores iniciales son 1, 1, 2, ya no admiten para suma 7 nada más que un 3.
Condicionamientos clásicos
Ya vimos en entradas anteriores sobre particiones que históricamente se han planteado algunos condicionamientos especiales a las particiones. Los recorremos de nuevo:
Función de partición Pk(N)
Es la misma función P(N) condicionada a que sólo intervenga un número K de sumandos:
Pk(N)= P(N / k sumandos): Particiones con un número k de sumandos fijado.
Con la hoja Cartesius es fácil programar esta función, ya que basta con definir XTOTAL=K, dejando el resto de condiciones igual.
Por ejemplo, evaluamos las particiones del número 12 en 4 sumandos, es decir p4(12):
xtotal=4
xt=1..12
creciente
suma=12
Resultan 15 particiones.
Función de partición Q(N)
Como la anterior, cuenta el número de particiones, pero en este caso se exige que los sumandos sean todos distintos. Por ejemplo, el entero 7 admite las siguientes particiones como números distintos: 7 = 6+1 = 5+2 = 4+3 = 4+2+1, luego Q(7)=5
Euler demostró que esta función coincide con el número de particiones de n en partes impares. Lo veremos más adelante.
La programación de esta función se consigue añadiendo la condición NO REPITE, para que todos los sumandos sean iguales. En el caso del 7 podríamos escribir:
xrango=7
xt=1..7
suma=7
creciente
no repite
Tendríamos el resultado siguiente:
Sólo son posibles las cinco particiones.
Particiones en partes impares P(N/Impar)
Introducimos este condicionamiento porque da lugar a un resultado obtenido por Euler:
El número de particiones de un número en sumandos distintos coincide con el de particiones en sumandos impares
Con Cartesius el planteo se limita a exigir que los sumandos sean impares. Basta condicionar los sumandos como una sucesión del tipo 2*n-1:
Obtenemos cinco particiones, el mismo número que nos dio el de sumandos distintos.
Podíamos haber usado un filtro, para que los sumandos sean impares:
Resultaría más rápido que el planteamiento anterior. Por último, otra posibilidad es definir los sumandos como un conjunto:
También es más rápido.
En otra futura entrada seguiremos condicionando las particiones de un número.







No hay comentarios:
Publicar un comentario