http://hojaynumeros.blogspot.com.es/2010/03/jugamos-con-sidon-y-golomb.html
Hoy lo hacemos con una de sus sucesiones. Se trata de esta:
1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12,…
http://oeis.org/A001462
También se la conoce como sucesión de Silverman. Como ves, es no-decreciente.
Tiene una definición muy curiosa, y es que a(n) representa el número de veces que aparece n en la sucesión, si además definimos a(1)=1 e implícitamente aceptamos que cada valor de n ocupa el mínimo número de orden posible.
Lo verás mejor si acompañamos cada valor con su índice:
La imagen de 1 es 1 por definición. La de 2 es 2 porque en la sucesión figura ese valor dos veces. También el 3 aparece repetido, por lo que a(3)=2. A(4)=3 debido a que aparecen tres cuatros, y así con todos.
Este es un ejemplo muy elegante de autorreferencia, pues se define un objeto como si ya estuviera construido, pero sólo lo podemos formar si seguimos la definición.
Si aceptamos la condición de que cada valor ocupe el primer número de orden que esté libre, y que cada nueva imagen es la menor que cumple a(n)>=a(n-1), esta sucesión es única. En efecto, nos ponemos a razonar:
A(1)=1 por definición, luego sólo existirá un 1 en la sucesión, por lo que la imagen de 2 no podrá ser 1. Según las condiciones, ha de ser 2, luego en la sucesión deberá haber un par de 2. Como hemos quedado en que se ocupan los menores números de orden, deberá quedar:
Esto significa que a(3)=2, luego también repetiremos el 3 dos veces:
Obligamos así a que el 4 y el 5 figuren tres veces:
Ya podrás seguir tú el razonamiento y completar la sucesión, que con las condiciones impuestas será única.
¿Lo podría conseguir una hoja de cálculo? La respuesta es afirmativa, y el algoritmo no es muy complejo. Necesitamos dos punteros, indi1, que recorrerá los valores de n, e indi2 que llevará la cuenta de los lugares que van quedando libres en la sucesión. Con indi1 se leen los valores, y con indi2 se escriben. Para evitar celdas vacías en los primeros valores, se rellenan el 1 y el 2. Quedará así con el Basic de las hojas:
Sub golomb()
Dim indi1, indi2, i, j, v
indi1 = 2 ‘El primer valor que se lee es el 2, en la celda (2,2)
indi2 = 2 ‘El primero que se escribe también es el 2
Cells(1, 2).Value = 1 ‘Rellenamos los dos primeros valores en las celdas (1,2) y (2,2)
Cells(2, 2).Value = 2
For i = 1 To 12 ‘Tomamos 12 valores, pero podían ser muchos más
v = Cells(indi1, 2).Value ‘Leemos el valor indicado por indi1 (que también es fila en la hoja)
For j = 1 To v ‘Escribimos tantos valores nuevos como indique v
Cells(indi2, 2).Value = indi1 ‘Todos los valores serán iguales a indi1
indi2 = indi2 + 1 ‘Avanza la escritura
Next j
indi1 = indi1 + 1 ‘Avanza la lectura
Next i
End Sub
Con esta subrutina se generará la sucesión de Golomb en la columna 2 de una hoja de cálculo:
Para mayor claridad hemos copiado los resultados en varias columnas, manualmente. Observarás que se reproducen fielmente los valores deseados.
La forma de generación de esta sucesión garantiza que a(n)<=n, ya que los valores de los números naturales aparecen “con retraso”, y cuando aparece el valor, el índice ha crecido más que él. El retraso se puede medir con la diferencia n-a(n):
Vemos que los retrasos a partir de 3 son todos positivos y crecientes.
Una propiedad elemental, pero que hay que pensar en ella un poco, es que las sumas parciales de esta sucesión coinciden con el índice de la última aparición en la sucesión del número de sumandos. Más claro: si sumo tres términos, 1+2+2=5, obtengo que la última aparición del 3 ocurrirá en el término 5. Esto es por la propia definición: el 1 aparece una vez, el 2 dos y el 3 otras dos, luego el último 3 aparecerá en el lugar 5.
La sucesión de sumas parciales es
1, 3, 5, 8, 11, 15, 19, 23, 28, 33, 38, 44, 50, 56, 62, 69, 76, 83, 90, 98, 106, 114, 122, 131, 140, 149, 158, 167, 177, 187,… (http://oeis.org/A001463) y coincide con el lugar de la última aparición de su número de orden. Así, si el quinto término es 11, ahí ocurrirá la última aparición del 5.
Según esto, si llamamos F(n) a los términos de la sucesión de Golomb y G(n) a sus sumas parciales, se cumplirá (estúdialo bien) que
F(G(n)) = n
Fórmula recurrente
Colin Mallows ha ideado una recurrencia muy atractiva para evaluar F(n):
F(1) = 1; F(n+1) = 1 + F(n+1-F(F(n)))
En hoja de cálculo las recurrencias son posibles, pero si se agota la pila de datos se puede bloquear el cálculo. Lo hemos intentado y funciona bien para los primeros términos, pero no va mucho más allá. En Basic sería
Public Function a(n)
If n = 1 Then
a = 1
Else
a = 1 + a(n - a(a(n - 1)))
End If
End Function
Con ella hemos formado esta tabla
En PARI también funciona la recurrencia, pero no merece la pena porque se va ralentizando para números grandes:
a(n)=if(n==1,1,1+a(n-a(a(n-1))))
{for(i=1,30,print1(a(i),", "))}
Aproximación asintótica
Por lo que hemos leído, no ha sido muy fácil llegar a esta expresión:
La comprobamos gráficamente
Se ve que son prácticamente indistinguibles.








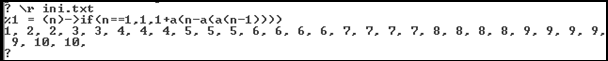


No hay comentarios:
Publicar un comentario