(Ver entradas anteriores sobre números semiprimos)
La búsqueda de los divisores semiprimos de un número N es similar a la de los divisores primos. Aquí deberemos buscar entre todos los números menores o iguales a N, pues existen semiprimos consecutivos y no nos podemos saltar ninguno.
Una forma sencilla de
identificar si un número k es divisor de N es exigir que N/k=N\k, porque
entonces la división normal “/” coincidirá con la entera “\”, lo que supone que
el resto de la división es cero. Si le añadimos la condición essemiprimo(k), ya los tendremos
identificados.
La siguiente función
construye el conjunto de divisores primos y los cuenta:
Function
div_semi$(n, repe As Boolean)
Dim k, m, nn, e
Dim s$
‘La función posee el
parámetro repe para detectar si un
divisor puede estar elevado a una potencia
If essemiprimo(n)
Then m = m + 1: div_semi = "1 : " + Str$(n): Exit Function ‘Casos primo y semiprimo
m = 0 ‘Contendrá el número de divisores
s = ""’Será la lista de divisores
k = 4 ’Comenzamos a ensayar semiprimos
While k <= n
If essemiprimo(k)
And n / k = n \ k Then ‘Es divisor
semiprimo
nn = n: e = 0 ‘Posibles exponentes
If repe Then ‘Caso de repetición
While nn / k = nn
\ k: e = e + 1: nn = nn / k: Wend
End If
If repe Then m =
m + e Else m = m + 1
s = s + Str$(k) ‘Recoge una nueva solución
If e > 1 Then
s = s + "^" + ajusta(e )’Exponente
End If
k = k + 1
Wend
s = ajusta(m) +
" : " + s ‘ajusta es como
Str$ sin espacio en blanco
div_semi = s
End Function
Para el caso de no contar repetidos, estos son los primeros valores. Los resultados se componen del número de divisores seguido de la lista de semiprimos:
El número de divisores está publicado en https://oeis.org/A086971En esa dirección figura un `programa en PARI sumamente
sintético:
a(n) = sumdiv(n, d, bigomega(d)==2)
También en ella se usa otra definición de estos divisores,
como aquellos semiprimos que dividen a N, pero a su cuadrado no.
La última igualdad vale 1 si es verdadera, por lo que la
suma se convierte en un conteo.
Para cualquier número elegido al azar disponemos de la misma
respuesta. Por ejemplo, el número 2160 posee este conjunto de divisores
semiprimos: 5 : 4 6 9 10 15, es decir, 5
divisores, 4, 6, 9, 10, 15.
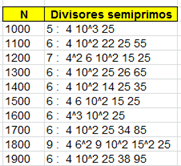
Podemos encontrar también la lista de divisores semiprimos
contando repeticiones, si en la función anterior usamos el parámetro 1. En la
siguiente tabla la hemos aplicado en números de cuatro cifras:
Versión numérica
En la función que usamos
podemos concretar la salida como el número de divisores nada más. De esa forma
podemos catalogar bien el objeto de la búsqueda. Por ejemplo, ¿Cuál es el primer número de cinco cifras
con seis divisores semiprimos sin repetir?
Las primeras soluciones
son
El primer número con seis
divisores es el 210, y sus divisores son 6, 10, 14, 15, 21 y 35. En la
dirección https://oeis.org/A220264 figuran los primeros de cada número de divisores.
Todos estos recuentos se
pueden realizar a partir de la descomposición factorial del número, como un
ejercicio de combinatoria elemental.
Por ejemplo, 210=2*3*5*7,
y basta agruparlos por pares: 2*3=6, 2*5=10, 2*7=14, 3*5=15, 3*7=21, 5*7=35.
Si existen factores
repetidos, hay que combinar con cuidado, para no repetir soluciones, En
540=2^2*3^3*5 iríamos construyendo 2*2=4, 2*3=6, 3*3=9, 2*5=10, 3*5=15.
Con la función div_semi y
parámetro 0: div_semi(540;0)= 5 : 4 6 9 10 15
Nota
En el conjunto de
divisores semiprimos no se puede definir un orden parcial múltiplo-divisor, ya que ningún semiprimo es múltiplo de otro. Por
eso, al contrario de los divisores generales, este conjunto no forma retículo.
Puedes consultar
https://hojaynumeros.blogspot.com/2013/05/reticulos-en-el-conjunto-de-divisores-1.html y siguiente.


No hay comentarios:
Publicar un comentario