Regresos 6 – Oblongos y pitagóricos (1)

 Desde la publicación de nuestra entrada de título “Oblongos y pitagóricos” (https://hojaynumeros.blogspot.com/2010/03/oblongos-y-pitagoricos-3.html) hemos estudiado algunas relaciones entre catetos e hipotenusa dentro de una terna pitagórica. Parece conveniente repasar las mismas, eliminando lo accesorio, y efectuar una síntesis de varias entradas.

Catetos que se diferencian en una unidad

Comenzaremos con un repaso a la primera cuestión que publicamos:

Una cuestión que ha dado juego desde los tiempos de Girard y Fermat y que permite recorrer alternativas de cálculo es la siguiente:

De todos los triángulos rectángulos de lados enteros ¿Cuáles cumplen que la diferencia entre los catetos es la unidad?

Recordábamos que la primera terna en cumplir esta condición es la popular 3, 4 y 5. El resto resultará de la ecuación x²+(x+1)²=y².

Otra forma de expresarlo es que el área del rectángulo formado por los dos catetos es un número oblongo, tipo N(N+1) y, por tanto, el área del triángulo será triangular (N(N+1)/2).

Podemos resolverla mediante búsqueda y con técnicas algebraicas.

Búsqueda

Como últimamente usamos funciones, organizaremos la búsqueda con la siguiente:

Function catetoscons$(n)

Dim a

Dim s$

s = ""

a = n^2 + (n+1)^2

If escuad(a) Then s = Str$(n) + Str$(n + 1) + Str$(Sqr(a))

catetoscons = s

End Function

 

Su funcionamiento se entiende bien: si n^2+(n+1)^2 es cuadrado, devuelve la terna completa. Las primeras conseguidas son:

Los valores de N están publicados en http://oeis.org/A001652. Volveremos a esta sucesión para revisar algunas propiedades.

Versión en PARI

Con este código avanzaremos más lejos en los valores de N:

is(n)={issquare(n^2+(n+1)^2)}

for(i=1,10^9,if(is(i),print1(i,", ")))

Obtenemos este resultado:

3, 20, 119, 696, 4059, 23660, 137903, 803760, 4684659, 27304196, 159140519,

Hemos llegado más lejos, pero con tantas cifras la búsqueda se hace muy lenta. Es preferible algún otro procedimiento más rápido, por lo que pasamos al Álgebra:

Estudio algebraico

La ecuación x²+(x+1)²=y² se puede desarrollar de esta forma: x²+(x+1)²=y²;  2x²+2x+1=y²; (2x+1)²+1=2y²; (2x+1)² - 2y² = -1, por lo que llamando z=2x+1 desembocamos en una ecuación de Pell con segundo miembro igual a -1

Z²-2y² = -1

Utilizamos la hoja de cálculo pell.ods o pell.xlsm contenidas en la dirección

http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm

con el resultado que indica la imagen siguiente

en la que valdrán las soluciones correspondientes a -1

Z=1;   Y=1;       Imposible, pues X sería negativo

Z=7;   Y=5         X=3; X+1=4; Y=5

Z=41; Y=29      X=20; X+1=21; Y=29

Z=239; Y=169   X=119; X+1=120; Y=169

Z=1393; Y=985 X=696; X+1=697; Y=985

Este método tiene el inconveniente de que depende de la precisión que tenga la hoja de cálculo en los números con coma flotante, lo que hará que se rompa en algún momento la periodicidad de los cocientes, en este caso el 2. Por ello se puede completar con una fórmula recursiva que obtenga soluciones exactas conociendo las primeras.

En este ejemplo cada elemento de las distintas celdas cumple la fórmula

a_n+2 = 2a_n+1 + a_n

pero como las soluciones aparecen de forma alternada, deberemos reiterar dos veces, y nos quedará:

a_n+4 = 2a_n+3 + a_n+2 = 2(2a_n+2 + a_n+1)+ 2a_n+1 + a_n = 4a_n+2 + 4a_n+1+ a_n = 6a_n+2 -  a_n

Con esta fórmula recursiva se van obteniendo las soluciones sin errores a partir de las dos primeras:

Z₀ = 1; Z₂ = 7; Z₄ = 6*7-1 = 41; Z₆ = 6*41-7 =239;…

Y₀ = 1; Y₂ = 5; Y₄ = 6*5-1 = 29; Y₆ = 6*29-5 =169;…

Pero no olvidemos que Z es una variable auxiliar Z=2X+1 y que después debemos despejar X

La siguiente lista de ternas, que coincide con la primera que propuso Girard, se ha obtenido mediante esta técnica. Los valores de N coinciden con los de la segunda columna.

1	0	1
5	3	4
29	20	21
169	119	120
985	696	697
5741	4059	4060
33461	23660	23661
195025	137903	137904
1136689	803760	803761
6625109	4684659	4684660
38613965	27304196	27304197
225058681	159140519	159140520
1311738121	927538920	927538921
7645370045	5406093003	5406093004
44560482149	31509019100	31509019101
259717522849	183648021599	183648021600
1513744654945	1070379110496	1070379110497
8822750406821	6238626641379	6238626641380
51422757785981	36361380737780	36361380737781
299713796309065	211929657785303	211929657785304

Los valores de N coinciden con los contenidos en http://oeis.org/A001652, que, por cierto, usa esta recurrencia como definición, que con el cambio de variable entre Z y X queda así:

a(n) = 6*a(n-1) - a(n-2) + 2 with a(0) = 0, a(1) = 3.

0, 3, 20, 119, 696, 4059, 23660, 137903, 803760, 4684659, 27304196, 159140519, 927538920, 5406093003, 31509019100, 183648021599, 1070379110496, 6238626641379, 36361380737780, 211929657785303,

Con hoja de cálculo ya no podemos seguir, por el problema de la coma flotante. Lo podemos intentar con PARI:

a=0;b=3;print1(a,", ");print1(b,", ");while(a<10^20,c=6*b-a+2;print1(c,", ");a=b;b=c)

Como llegamos a 10^20, en pocos segundos se avanza en la lista de valores de N:

Una curiosidad

Cuando no se tienen claras las fórmulas de recurrencia lineal, pero se dispone de suficientes términos iniciales. Se puede acudir a mi hoja de cálculo ecurrecurre, disponible en la dirección

http://www.hojamat.es/blog/ecurrecurre.xlsm

En este caso usamos como datos los términos iniciales 0, 3, 20, 119, 696, y elegimos la variedad “No homogénea”, para que admita el sumando independiente 2. Pulsamos el botón de resolver y nos devuelve los coeficientes 6, -1 y 2.

Recurrencia doble

Fermat propuso una fórmula de recurrencia para generar ternas de este tipo a partir de otras similares. Dada la terna (x,x+1,y), se puede generar otra similar (x’,x’+1,y’) mediante las fórmulas x’=2x+3y+1  y y’=4x+3y+2.

Cuando se buscan las soluciones de la ecuación de Pell las recurrencias vienen dadas por las fórmulas de recurrencia z_n+1=z_n*z₀+D*y_n*y₀  y_n+1=z_n*y₀+y_n*z₀, pero en el caso z²-2y² = -1 las soluciones surgen de forma alternada.

Así, como en este caso z₀=1, y₀=1, tendremos:

z_n+1=z_n+2y_n; y_n+1=z_n+y_n  y reiterando dos veces

Z’’=Z’+2Y’=(Z+2Y)+2(Z+Y) = Z+2Y+2Z+2Y = 3Z+4Y

Y’’=Z’+Y’ = Z+2Y+Z+Y = 2Z+3Y

Teniendo en cuenta que Z=2X+1, y que Y=X+1, nos resulta

Y’’=2Z+3Y=2(2X+1)+3Y = 4X+3Y+2, que es la segunda fórmula de Fermat

De Z’’=3Z+4Y podemos obtener (2X’’+1)=3(2X+1)+4Y;  2X’’ = 6X+4Y+2;

X’’ = 3X+2Y+1, que es la primera

Aplicamos estas dos fórmulas al cateto menor y a la hipotenusa y obtenemos los mismos resultados a partir de 3, 4 y 5

X''=3X+2Y+1        X+1   Y''=4X+3Y+2

3        4        5

20      21      29

119   120   169

696   697   985

4059 4060 5741

23660 23661 33461

137903 137904   195025

803760 803761   1136689

4684659 4684660 6625109

27304196  27304197  38613965

159140519 159140520 225058681

 Uso de la generación de ternas

 La terna 3, 4, 5 está engendrada por las fórmulas clásicas 2uv, u²-v² y u²+v² para u=2 y v=1. Si sustituimos u y v por u, v+2u se mantendrá la misma diferencia entre catetos.

Basta ver que si engendramos los nuevos catetos y los restamos (en orden contrario) resultará: 2u(v+2u) - (v+2u)²+u²= 2uv+4u²-v²-4u²-4uv+u² = u²-v²-2uv, que es la diferencia original.

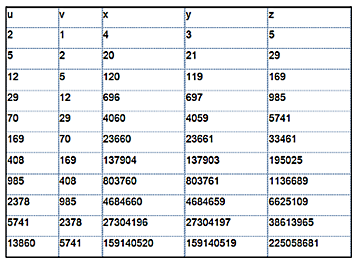
Esto nos permite engendrar de nuevo la lista que estamos considerando, tomando, n primer lugar u=2 v=1, y generando con ella la primera terna 3, 4 y 5. Después se aplica la fórmula de recurrencia  u_n = 2u_n-1+v_n-1 v_n = u_n-1 y se vuelve a generar una terna con ella, que resultará tener la misma diferencia pero con signo cambiado. Así hemos generado la lista con hoja de cálculo:

Con este cálculo abandonamos los algoritmos, y en la siguiente entrada pasaremos a propiedades curiosas de este tipo de ternas.