Diferencias de cubos enteros positivos

Algunos números enteros positivos son diferencia de dos cubos, también enteros y positivos. Por ejemplo, 3367 lo es de tres formas diferentes: 3367=34³-33³=16³-9³=15³-2³. Otros números, como 8624, no coinciden con ninguna diferencia de  cubos. En esta entrada aprenderemos a descubrir ejemplos y estudiar algunos casos especiales.

Cuando se trata con diferencias, el estudio previo que se debe emprender es el de encontrar una cota para los números que se restan. En este caso, además de ello, podremos añadir una condición que deban cumplir minuendo y sustraendo. Es un tema algebraico sencillo en este caso. Llamemos a+k a la base del cubo mayor y a a la del menor, siendo además N el valor de la diferencia entre ambos cubos. Tendremos entonces:

(a+k)³- a³ = 3a²k+3ak²+k³ = k(3a²+3ak+k²) = N

Esta igualdad nos indica que N ha de ser múltiplo de k. Esto nos da una cota para la diferencia entre bases, junto con la condición de que sea un divisor de N. Por otra parte, no es difícil acotar las bases de los cubos:

3a²+3ak+k² = N/k

3a² < 3a(a+k) = N/k-k² < N/k

De aquí deducimos que una cota de a es la raíz cuadrada de N/(3k)

Si recorremos los valores de los divisores de N, obtendremos valores posibles de k, y con esta cota podremos encontrar valores de a para comprobar si (a+k)³- a³ = N

Estas condiciones se usan en la siguiente función de VBasic, que nos devolverá las descomposiciones en diferencia de cubos que presente un número N:

Function difcubos$(n)

Dim k, a, t, m
Dim s$

s = "" ‘Contenedor de soluciones
m = 0 ’Número de soluciones
For k = 1 To n / 2
If n / k = n \ k Then ‘k ha de ser divisor de N
t = Sqr(n / k / 3) ‘Cota para a
For a = 1 To t

If (a + k) ^ 3 - a ^ 3 = n Then m = m + 1: s = s + "a=" + Str$(a) + " k=" + Str$(a + k) ‘Si es una solución, se incorpora
Next a
End If
Next k
If s = "" Then difcubos = "NO" Else difcubos = ajusta(m) + " " + s ‘Si no hay solución devuelve un NO
End Function

Con esta función encontraremos los números enteros que son diferencia de cubos, con el dato del número de soluciones que presenten. Por ejemplo, en la siguiente tabla figuran los resultados desde 720 hasta 730:

Observamos que sólo dos números cumplen la condición, y, en este caso, con dos soluciones cada uno. Las diferencias son divisores de N. En el caso de 721, son 1 y 7, y, en el caso de 728, 2 y 8, divisores en ambos números.

Una idea nos viene al momento, y es que si N es primo, la única diferencia posible es 1:

Si un número primo es diferencia de dos cubos, ambos han de ser consecutivos.

Lo comprobamos con la función anterior añadiendo la condición de ser primo:

Se trata de los “primos cubanos”, que son objeto de estudio en otra entrada en nuestro blog

(ver https://hojaynumeros.blogspot.com/2024/03/primos-cubanos.html

Están publicados también en https://oeis.org/A002407

Los primeros números que son diferencia de cubos de una, dos o tres formas son estos:

7, 19, 26, 37, 56, 61, 63, 91, 98, 117, 124, 127, 152, 169, 189, 208, 215, 217, 218, 271, 279, 296, 316, 331, 335, 342, 386, 387, 397, 448, 469, 485, 488, 504, 511, 513, 547, 602, 604,

Están publicados en https://oeis.org/A038593, y parece ser que serán muy raros los que presenten más de tres soluciones. Como en nuestra función el primer carácter representa el número de soluciones, no es difícil separar esta tabla según este dato.

Una sola solución:

https://oeis.org/A014439

Dos diferencias de cubos:

https://oeis.org/A014440

Tres diferencias:

Observamos que van disminuyendo los casos.

Ver https://oeis.org/A014441

Segunda versión de búsqueda

En la función propuesta hemos usado un bucle de búsqueda para k y otro para a. Este último se puede evitar despejando a en 3a²+3ak+k²-N/k. Así lo hemos efectuado en PARI, y se consigue más velocidad de proceso, pero para números con tres soluciones sigue siendo lento. Lo copiamos aquí por si alguien desea experimentar:

difcubos(n)={my(m=0,k,a,q);for(k=1,n/2,if(n%k==0,q=9*k^2-12*(k^2-n/k);if(issquare(q),a=(-3*k+sqrt(q))/6;if(a==truncate(a)&&a>0,m+=1))));m}

for(i=1,10^6,if(difcubos(i)==3,print(i)))

Se exige en él que a sea entera y positiva. Cambiando el 3 de la última línea se puede intentar buscar números con cuatro soluciones, si se dispone de un equipo potente.

Casos particulares en la diferencia

En nuestras publicaciones en Twitter o X nos aparecen casos en los que un cuadrado y un cubo están relacionados por una identidad. En este apartado comenzaremos por estudiar el caso en el que una diferencia de cubos es cuadrada. Para ello cambiaremos un poco nuestra función básica, en el sentido de exigir al principio que N sea un cuadrado. El resultado, ya conocido, es

La segunda columna está publicada en https://oeis.org/A038597

Hay un caso interesante en la tabla, y es 14^3-7^3=7^4, y esto nos anima a buscar otras diferencias entre cubos que sean potencia de cualquier exponente. Para ello disponemos de la función en Excel ESPOTENCIA, que devuelve el exponente mínimo de una potencia, o cero si no es de ese tipo. Con ella encontramos diferencias que son cuartas potencias:

Con esta búsqueda hemos descubierto una propiedad interesante: si N es diferencia entre dos cubos, su cuarta potencia también lo es:

La razón es sencilla: Si en una diferencia de cubos con resultado N multiplicamos ambos cubos por N³, resultará otra diferencia de cubos con resultado N⁴. Ocurrirá igual con N⁷ o N¹⁰.

Podemos observar que los datos de la cuarta columna coinciden con los de la segunda multiplicados por N.

Otros tipos de diferencias de cubos

Esta última parte del estudio la desarrollaremos con brevedad salvo que surja alguna propiedad interesante.

Diferencias que son números primos

Ya advertimos que, en este caso, las bases de los cubos han de ser consecutivas y los primos son los llamados “cubanos”:

Diferencias de cubos triangulares

Los primeros son estos:

No descubrimos particularidades, luego pasamos a otro caso.

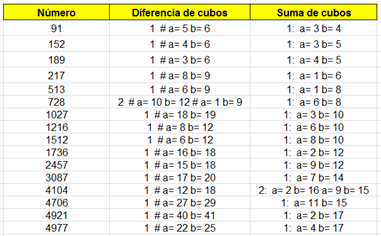
Diferencia de cubos igual a suma de cubos

Aprovechando una pequeña función disponible, SUMCUBOS, se puede exigir que la diferencia de cubos coincida con la suma de otros dos. Los primeros resultados son:

Están publicados en https://oeis.org/A225908

Como se señala en esta página, estos datos dan lugar a identidades en las que un cubo es suma de otros tres, pues basta pasar de miembro el cubo que aparece restando:

6^3-4^3=3^3+5^3 da lugar a 6^3=3^3+4^3+5^3.

Esto explica que en la segunda columna aparezcan repetidos tres veces algunos cubos mayores de cada caso, como el 6, el 9 o el 12, ya que la suma da lugar a tres diferencias.