Medias de tres primos consecutivos

Puede ser interesante estudiar la media aritmética de tres números primos consecutivos. En algunos casos, coincide con el primo central, que en ese caso sería equilibrado. No es esto infrecuente, pues los primos pueden ser del tipo 4k+1 o 4k-1, y también 6k+1 y 6k-1, además de otras pautas. También puede ocurrir que la media sea un tipo especial de número, como cuadrado, triangular u oblongo. Organizaremos búsquedas ordenadas y, entre ellas aparecerán casos que ya estén estudiados o que presenten propiedades interesantes.

Primo equilibrado

Con cualquier lenguaje de programación bastará exigir que

(prevprime(n)+n+postprime(n)/3=n

Se entiende que prevprime y postprime son los primos adyacentes a n. En todos los lenguajes se usan palabras similares. En este blog usamos PRIMANT y PRIMPROX, para hojas de cálculo.

Así que nuestra función para detectar primos equilibrados será:

Function primoequil$(n)

Dim s$

s = ""

If esprimo(n) Then

If (primant(n) + n + primprox(n)) / 3 = n Then s = Str$(primant(n)) + " ; " + Str$(primprox(n))

End If

primoequil = s

End Function

Le hemos dado carácter de string para que recoja los dos primos adyacentes.

Los primeros primos de este tipo son

Junto a cada uno figuran sus dos primos contiguos. Podemos añadir las diferencias con el centro, para más información.

Estos números están publicados en http://oeis.org/A006562

5, 53, 157, 173, 211, 257, 263, 373, 563, 593, 607, 653, 733, 947, 977, 1103, 1123, 1187, 1223, 1367, 1511, 1747, 1753, 1907, 2287, 2417, 2677, 2903, 2963, 3307, 3313, 3637, 3733, 4013, 4409, 4457, 4597, 4657, 4691, 4993, 5107, 5113, 5303, 5387, 5393,…

En la tabla de arriba, salvo el caso especial de 3, 5 y 7, todas las diferencias son múltiplos de 6 ¿Será así siempre?

En este mismo blog ya se ha razonado la respuesta afirmativa:

Las diferencias, salvo en el 5, son múltiplos de 6. La razón es que a partir del 5 todos los primos son del tipo 6n+1 o 6n+5. En las ternas que se forman tienen que ser todos del mismo tipo, ya que si el primero es 6n+1 y el segundo 6m+5, el tercero tendría el tipo 6m+5+(6k+4)=6h+3, no primo. Igualmente, si el primero es tipo 6n+5 y el segundo 6m+1, el tercero sería 6m+1+(6h+2). Lo puedes ver con Z₆: Si el primero tuviera resto 1 y el último resto 5, el promedio presentaría resto 3 y no sería primo. Igual con los otros casos.

https://hojaynumeros.blogspot.com/2015/07/formas-de-ser-un-numero-equilibrado-3.html

Por ejemplo, el primer primo que es media entre su anterior y posterior con diferencia 30 es 69623, que forma la progresión (69593, 69623, 69653)

Se ha conjeturado que existen infinitos primos equilibrados.

Desviaciones respecto al equilibrio

Si el primo central no es equilibrado, la media será mayor o menor que él, se desviará una “distancia” o diferencia. Salvo con el 2, siempre será par.

Podemos introducir esa distancia como parámetro en la función anterior:

Function primoequil(n, d)

Dim s, m

s = 0

If esprimo(n) Then

m = (primant(n) + n + primprox(n)) / 3 - n

If m = d Then s = m

End If

primoequil = s

End Function

Tal como está planteado, se desecharán las medias que no sean enteras, y el resultado será 0. Así que esta función devuelve un cero si no se da la diferencia dada, o esa diferencia si es válida. Por ejemplo, con ella hemos encontrado los primeros números en los que la media sobrepasa al primo central en 2 unidades:

No abundan las diferencias grandes: el número 5749 es el primero que presenta una diferencia de 8, porque la media es 5757. De igual manera, 15823 es el primero que presenta diferencia 10. Estos son los siguientes:

40289         d=16

45439         d=12

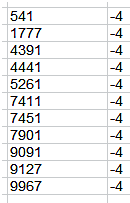
Podíamos buscar diferencias negativas:

Estos son los primeros primos con diferencia -4 (para ello hay que cambiar la declaración de variables a integer)

Media triangular

Podemos ahora investigar cómo son las medias entre tres números primos consecutivos, de qué tipo son. Las más interesantes son las de tipo polinómico, como triangulares, cuadradas y cúbicas. Recorreremos estos tres tipos abordando la búsqueda desde dos puntos de vista. Por un lado nos basaremos en los tres primos consecutivos, y, por otro, en los valores de N en los que se basan las fórmulas polinómicas.

Comenzamos con medias triangulares. Elegimos primos, y le calculamos la media de ellos con los dos siguientes. Si es triangular, la aceptamos. Usaremos PARI porque los números a manejar serán grandes.

El criterio para saber si un número es triangular es el conocido de que 8*n+1 sea cuadrado. De esta forma, la búsqueda queda así en PARI:

18713, 27253, 35227, 45433, 138587, 251677, 283861, 425489, 462221, 463189, 486583, 634493, 694409, 826211, 943231, 1103341, 1163557, 1181927, 1214453, 1282387, 1462891, 1509439, 1925681, 1931569,…

(Publicados en http://oeis.org/A226150)

Hemos usado aquí, en la web de PARI/GP https://pari.math.u-bordeaux.fr/gp.html un código mucho más simple que en la página enlazada:

ok(n)={my(m=nextprime(n+1),p=nextprime(m+1),r=(n+m+p)/3);isprime(n)&&issquare(8*r+1)}

for(i=2,2*10^6,if(ok(i),print1(i,", ")))

El otro procedimiento consiste en ir recorriendo los números triangulares n(n+1)/2 y detectar los primos más cercanos consecutivos. Como vimos en la primera parte de este estudio, la media de tres primos puede caer a la derecha o a la izquierda del central, por lo que esa detección se ha de efectuar dos veces. En este listado para Excel se comprende bien:

Function media_tres_prim(n)

Dim a, p, q, r, s, u, v, m

m = 0

a = n * (n + 1) / 2 ‘Se construye el número triangular

p = primprox(a): q = primprox(p): r = primant(a): s = primant(r)

u = (p + q + r) / 3: v = (s + r + p) / 3’Se estudian dos posibles medias

If u = a Then m = r ‘La media queda a la derecha

If v = a Then m = s ‘O a la izquierda

media_tres_prim = m

End Function

De una forma bastante rápida se reproduce el listado anterior y, además, nos devuelve los órdenes N de los números triangulares

Se comprende que es un método mucho más eficiente. Los números de la primera columna están publicados en http://oeis.org/A226147

 

Media cuadrada

Para encontrar casos con media cuadrada, bastará cambiar n(n+1)/2 por n^2 en Excel y 8*n+1 por n en PARI

En Excel nos resultarían:

 

Las bases de la primera columna están publicadas en http://oeis.org/A226146

En PARI, el primer primo resulta así:

ok(n)={my(m=nextprime(n+1),p=nextprime(m+1),r=(n+m+p)/3);isprime(n)&&issquare(r)}

for(i=2,1600000,if(ok(i),print1(i,", ")))

Simplemente hemos sustituido issquare(8*r+1) por issquare(m)

Media cúbica

Cambiando n^2 o n*(n+1)/2 en la función de arriba por n^3, resultan las bases y los primos iniciales de la terna para este caso:

53      148867

131   2248069

179   5735291

219   10503443

227   11697073

419   73560043

489   116930119

633   253636087

733   393832819

913   761048471

925   791453099

1021 1064332237

1223 1829276531

1247 1939096199

1263 2014698431

Y su código en PARI:

ok(n)={my(m=nextprime(n+1),p=nextprime(m+1),r=(n+m+p)/3);isprime(n)&&ispower(r,3)}

for(i=2,10^7,if(ok(i),print1(i,", ")))

Por terminar las búsquedas, nos quedamos con las potencias cuartas:

Cuarta potencia

7        2393

35      1500613

69      22667111

85      52200611

91      68574943

117   187388689

 

Queda a los lectores el reto de adaptar el código para este caso y probar otros números poligonales.