El día 29/12/19 descubrí este tweet de @d_r_o_n_e:
En él podemos ver un ejemplo que puede reproducirse mediante
el uso de la “fuerza bruta”, herramienta que aparece en este blog muchas veces,
aunque no se confiesen todas. Consiste en recorrer todas las variantes de un
problema sin usar razonamientos ni condiciones complementarias. Es una buena
estrategia comenzar con esta forma de buscar para después ir afinando
resultados, explicarlos y, si es posible, justificarlos.
Uso de la
herramienta Cartesius
Nuestra herramienta Cartesius también ayuda a combinar
variables de todas las formas posibles, pero se hace lenta cuando nos acercamos
al rango de los números de cuatro cifras. La puedes descargar desde
Con ella hemos intentado este planteo:
XTOTAL=3
XT=1..200
ES
X1*X2*X3/1000=X1+X2+X3
CRECIENTE
Es fácil entender su significado: combinaremos tres
variables, todas entre 1 y 200, de forma que se cumpla la condición pedida y después
nos quedamos con las crecientes. Al cabo de más de media hora se obtuvo esta
tabla, completada en sus dos últimas columnas con las dos expresiones que deben
coincidir.
Observamos, y lo confirmaremos un poco más abajo, que
aparecen repetidas algunas soluciones menores que 444, como son 231 o 240. Con
el planteo propuesto se encontraron 32 soluciones, de las que solo hemos
reproducido las primeras. Aparecen en orden inverso al natural porque cuando
unos factores tienen igual suma, su producto crece cuando sus diferencias son
menores. Con este intento descubrimos ya que la técnica de la “fuerza bruta” es
muy lenta en producir resultados.
Analizando la búsqueda descubrimos que Cartesius ha tenido
que analizar 200*200*200 =8*10^6 números, y en cada uno calcular si una
igualdad se verifica o no. Eso es mucho para un portátil normal. Ahí es donde
falla la fuerza bruta, en la multiplicación de casos que produce la
Combinatoria.
Algoritmos
La “fuerza bruta” se caracteriza casi siempre por el uso de
bucles del tipo FOR_NEXT, WHILE o REPEAT, casi siempre anidados en tres o
cuatro niveles.
Lo normal, en ejemplos similares al que nos ocupa, es
disponer de tres bucles anidados, con la propiedad deseada en el interior de
los tres. Comenzaremos exigiendo solo una condición de las propuestas por
@d_r_o_n_e
En este caso podíamos comenzar por este código:
Sub fuerzabuta()
Dim i, j, k, a, b, fila
fila = 10
‘La fila determina la construcción de una tabla en Excel
For i = 1 To 1000 ‘Bucle triple
For j = 1 To i
For k = 1 To j
a = i + j + k ‘Cálculos previos
b = i * j * k / 1000
If a = b Then ‘Condición pedida
fila = fila + 1: ‘Construcción de la
tabla
ActiveWorkbook.ActiveSheet.Cells(fila,
2).Value = b
ActiveWorkbook.ActiveSheet.Cells(fila,
3).Value = i
ActiveWorkbook.ActiveSheet.Cells(fila,
4).Value = j
ActiveWorkbook.ActiveSheet.Cells(fila, 5).Value
= k
End If
Next k
Next j
Next i
End Sub
Hemos ejecutado esta macro de Excel y nos han
resultado muchas soluciones. Lo que nos interesa es que salgan repetidas. Por
la forma de plantear el problema, aparecerán desordenadas. Las primeras han
sido:
Coinciden con las obtenidas en Cartesius. Observamos
su falta de orden y la existencia de un repetido, el 189. Según la tabla:
189=84+75+30=84*75*30/1000
189=100+54+35=100*54*35/1000
Es una solución también más pequeña que la
propuesta de 444.
Para verlas todas ordenaremos la columna y así se
verán mejor los repetidos. Con este método hemos descubierto los siguientes:
189, 207, 231, 240, 255, 273, 297, 420, 444, 480, 504, 741, 759, 768, 810,
891,… De ellos presentan soluciones triples 231, 504 y 891.
Más fuerza
bruta (o menos)
Podíamos intentar descubrir tan solo los números
en los que se da más de una solución. El problema es que para esto se
necesitaría un bucle más, con el consiguiente aumento de tiempo de proceso. Es
el coste de utilización de bucles múltiples sin apenas condicionamientos. Hay
una forma de evitar un nuevo bucle, y es considerar que en el algoritmo
anterior hemos hecho variar el valor de k
cuando en realidad está condicionado por la igualdad que se pide a=i+j+k.
Considerándolo así, lo único que ha de cumplir k es que su valor sea a-i-j
y, por cuestión de unicidad, que no sea mayor que j. Esto es lo que hemos implementado en PARI:
for(n=1,500,m=0;b=0;for(i=1,n,for(j=1,i,c=i+j;if(c<=n&&n-c<=j,b=i*j*(n-c)/1000;if(b==n,m+=1))));if(m>1,print1(n,",
")))
Mantenemos los bucles con las variables i y j.
Eliminamos el bucle de k sustituyéndolo por la expresión b=i*j*(n-c)/1000 y
concretamos las condiciones que ha de cumplir. Con la variable m exigimos que haya repetición de
casos. Hemos añadido un nuevo bucle, pero con los cambios apenas se resiente la
velocidad del proceso. De todas formas, para rangos de números de 1000 más o
menos, puede tardar muchos minutos o incluso más de una hora. Cosas de la
fuerza bruta.
Los primeros resultados son:
189, 207, 231, 240, 255, 273, 297, 420, 444, 480,
504, 741, 759, 768, 810, 891, 1221, 1320, 2418,…
Con esto damos por terminada la búsqueda, porque
la fuerza bruta cansa y no se aprende mucho con ella.
Rebajamos
pretensiones
Podíamos exigir productos similares, pero con solo
dos variables, es decir, N=i+j=i*j/100. Esto simplifica el problema, y solo lo
incluimos como repaso de las técnicas empleadas anteriormente. Las
explicaciones para el caso anterior valen también para este.
Con
Cartesius
Plantearíamos, por ejemplo:
xtotal=2
xt=1..700
es x1+x2=x1*x2/100
creciente
Obtendríamos:
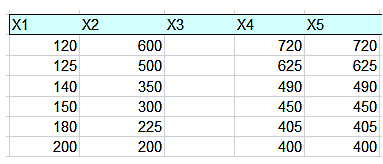
Las primeras columnas corresponden a los valores
de i, j y las siguientes el valor repetido de N.
Así, 120+600=120*600/100=720
125+500=125*500/100=625
En principio, no parece que existan soluciones
dobles.
Con una
función de Excel:
Function esmultiple2(n)
Dim i, j, k, a, b, m
m = 0
For i = 1 To n
For j = 1 To i
a = i + j
b = i * j / 100
If a = b And a = n Then m = m + 1
Next j
Next i
esmultiple2 = m
End Function
Esta función cuenta las veces en las que se da la
igualdad i+j=i*j/100. Organizando una búsqueda nos resulta:
Tampoco se aprecian repetidos
Con PARI
Traducimos la función anterior a PARI y la
integramos en un bucle de búsqueda:
for(n=1,10000,m=0;b=0;for(i=1,n/2,b=i*(n-i)/100;if(b==n,m+=1));if(m>0,print1(n,",
")))
Volvemos a obtener los mismos resultados:
400, 405, 450, 490, 625, 720, 841, 1210,
1458, 2205, 2704, 5202,…
Tampoco aquí se detectan repetidos. Lo dejamos
como complemento.




No hay comentarios:
Publicar un comentario