Simulación
normal
Seguimos hoy la serie de simulaciones que iniciamos en
En esas entradas vimos la distribución uniforme y la de
Bernouilli. Hoy lo haremos con la normal.
Nos basaremos en esta también en las prácticas de nuestro
curso de Estadística, (http://www.hojamat.es/estadistica/iniestad.htm)
adaptándolas al formato de un blog. Usaremos nuestro Simulador implementado
para hojas de cálculo, el cual puede sufrir cambios a lo largo de la serie, por
lo que se aconseja su recarga en caso de duda.
Distribución
normal
Si no recuerdas la distribución normal puedes acudir a la
Teoría correspondiente
Por ahora basta con saber que siguen esa distribución normal
de forma aproximada muchos datos tomados de nuestra vida diaria:
- Magnitudes que dependen de muchas causas independientes, cuyos efectos se suman y cualquiera de ellas aislada tenga efectos despreciables.
- Distribuciones de errores en las medidas.
- Medidas de tipo antropológico (estaturas, pesos, inteligencia...) y biológico (glucemia, nivel de colesterol...)
- Límite de otras distribuciones estadísticas cuando n aumenta.
- Todas ellas producen gráficos con forma de campana de Gauss, más o menos aproximada.
Nuestro simulador puede producir datos aleatorios que sigan
esta distribución normal.
Puedes descargarlo para Excel
Y para LibreOffice Calc
Esta herramienta está en desarrollo, por lo que debes
ignorar las hojas no terminadas.
La forma más práctica de plantear una simulación de este
tipo es la de dar el promedio de los datos y la desviación típica, pero también
funciona conociendo el mínimo y el máximo esperados.
Lo vemos con algún ejemplo:
Los de más altura
En un Centro de Enseñanza se han tallado todos los alumnos y
alumnas de un nivel, 128 en total y ha quedado como estatura mínima la de 140
cm, y como máxima, 198 cm. Si deseamos seleccionar a aquellas personas con
estatura superior a 180 cm. ¿Cuántas esperaremos encontrar?
La teoría estadística puede responder a esta pregunta
mediante las propiedades de la distribución normal. Aquí lo intentaremos con el
Simulador:
Hemos concretado lo siguiente:
- · Distribución normal con decimales (son estaturas) usando máximo y mínimo
- · Mínimo 140 y máximo 198
- · Una columna de 128 filas (número de alumnos y alumnas)
- · Diez intervalos
Procura localizar bien todos esos datos en sus celdas
correspondientes. Pulsa el botón “Simulador”.
Con este planteamiento la simulación se aproximará bastante
a las medidas reales. Si pasas a la segunda hoja advertirás la forma típica de
campana de esta distribución, y que la estatura media es aproximadamente de 169
cm., y la desviación típica cercana a 8. No podemos pretender resultados
idénticos a los previstos por la teoría, pero comparando los estadísticos de la
simulación con los valores teóricos, vemos que existe una buena aproximación.
La gráfica también tiene forma aproximada de campana, aunque
con tan pocos elementos de simulación, nunca seguirá ese tipo teórico:
También, de paso, hemos descubierto que esperaremos unas 12 personas
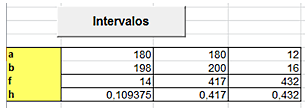
con más de 180 cm. Afinamos esto más. Busca el apartado de Intervalos en la hoja de
resultados
Con esta tabla podemos contar fácilmente resultados sin
tener que recorrerlos.
Tiene un funcionamiento simple, y es el de escribir en
la columna correspondiente (en nuestro caso la primera, porque solo hay una)
los extremos entre los que deseamos contar resultados. En nuestro caso serían
180 y 198, que es el máximo. Ahora basta con pulsar el botón Intervalos y nos
devolverá la frecuencia absoluta, 14, y la relativa, 0,11 aproximadamente, un
11%.
Repitiendo la simulación han resultado, en varios intentos,
15, 11, 8, 11 y 15, por lo que juzgamos
que lo más probable es que nos encontremos con unos 11, lo que nos permitirá
organizar un equipo de baloncesto, si ese era el objetivo.
Si conoces algo de la teoría de esta distribución, sabrás
que existen funciones y tablas que te devuelven este dato de forma teórica,
pero nuestro objetivo estaba en recoger los datos de una simulación, no en
prever el resultado. En nuestro caso, y no seguiremos con el tema, la
aproximación sería:
1-DISTR.NORM.N(180;169;8,2857;1)=0,092157044
Un poco menor que la obtenida del 11%, en este caso un 9,2%.
Así funcionan los resultados en las simulaciones. Nunca esperes aproximaciones
destacables.
Un ejemplo con media
y desviación típica
Una población de 500 personas con riesgo de diabetes en una
ciudad ha presentado un promedio de 106 mg/100ml de nivel de glucosa en sangre
y una desviación típica de 8 mg/100ml. Diseñar una simulación para encontrar a
partir de qué nivel encontraremos las 50 personas con más riesgo.
Organizamos la simulación, pero usando ahora media y
desviación típica:
Obtendremos una columna con 500 niveles de glucosa y una
distribución en forma de campana de Gauss.
En nuestra simulación se obtuvieron media y desviación
bastante cercanas a las teóricas:
Si ahora deseamos obtener los cincuenta niveles más altos,
nos bastará con ordenar la columna G de la primera hoja (de mayor a menor) y
observar n qué nivel se encuentra el número 50:
Vemos que hay que comenzar por el nivel 116,4 para así poder
seleccionar los 50 posibles pacientes con más riesgo. Si repites la simulación
varias veces podrás quedarte con una media más aproximada.
También podemos trabajar con los intervalos cambiando el
mínimo hasta obtener un resultado aproximado de 50 personas. En otra simulación
nos da un tope de un nivel de 114 o 115:
INV.NORM(0,9;106;8)=116,25
Hemos tomado de probabilidad 0,9 porque los 50 en una
simulación de 500 representa un 10% superior y un 90% inferior. Nuestra
simulación se queda un poco corta.
Medidas válidas
En una medición con mucho riesgo de errores se ha decidido
rechazar aquellas medidas que se alejen de la media más de una desviación
típica y media. Supongamos que en mediciones anteriores resultó una media de 65
y una desviación típica de 8. ¿Qué número aproximado de mediciones debemos
efectuar para garantizarnos 200 medidas catalogadas como válidas, si la
distribución en la población se puede considerar normal?
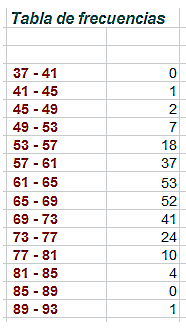
De nuevo acudimos a una simulación. Según los datos que nos
dan, las medidas válidas estarán entre 65-3*8/2 y 65+3*8/2, es decir, entre 53
y 77. Comenzamos una simulación de 250 mediciones y concretamos 14 intervalos.
Observamos, de forma aproximada, que habría que desechar
unas 10 medidas inferiores y unas 15 superiores, lo que nos daría 250-10-15=225
medidas válidas.
Esta observación se confirma también con intervalos:
Probamos con 230 simulaciones, pare ver si nos acercamos a
200 válidas.
Después de la simulación hay que desechar 16+18=34, con lo que nos quedamos cortos, 196. Subimos y bajamos el número de simulaciones y 230 parece quedar en la media, luego es aconsejable usar muestras de 230 medidas.
Después de la simulación hay que desechar 16+18=34, con lo que nos quedamos cortos, 196. Subimos y bajamos el número de simulaciones y 230 parece quedar en la media, luego es aconsejable usar muestras de 230 medidas.
Esto ha sido una especie de juego. Si acudimos a la
distribución normal teórica, descubriremos que el porcentaje esperado de
medidas que se alejen más de 3/2 de desviación típica por un lado es de 0,066807201.
Por los dos lados será 0,133614403, y restando de 1, el porcentaje de medidas
válidas sería 0,866385597. Dividimos 200 entre ese porcentaje y obtenemos 230,844096.
Nuestra simulación no estaba descaminada.
Nuestra simulación no estaba descaminada.
Con este experimento también hemos aprendido que los
porcentajes no dependen de una media concreta sino de la medida tipificada Z,
que en este caso valía Z=1,5.
Obtención
de muestras
En el caso de la distribución normal es muy interesante el
disponer de muestras de un colectivo del que sabemos algunos parámetros
(generalmente media y desviación típica). Vemos algunos ejemplos:
Distribución de
errores
75,6 78,0 77,8 77,5
75,2 79,0 76,8 78,0
76,5 76,8 76,6 77,2
77,3 78,4 76,6 76,6
77,1 77,6 77,3 76,1
Los datos anteriores simulan 20 repeticiones de una medida.
A simple vista parece que la media es 77. En el Simulador se ha obtenido media
77,1 y desviación típica 0,9. Esta tabla puede servir para que el alumnado
obtenga también la media, la desviación
típica y la gráfica, para saber si se aproxima a la distribución normal. Con el
Simulador se pueden preparar rápidamente distintas muestras para un trabajo por
equipos. También puede aprenderse en
clase el funcionamiento de esta herramienta y que los grupos simulen su propia
muestra.
Colesterol en sangre
Esta muestra ha sido generada mediante el Simulador:
221,0 205,9 208,2 224,8 205,3 209,7 220,8 229,7
202,8 215,2 203,6 240,7 215,8 236,4 234,6 213,6
189,0 212,7 197,4 203,2 175,4 218,4 227,6 222,4
246,2 238,8 211,5 229,4 206,4 195,8 179,4 206,3
220,4 234,2 207,5 184,7 204,5 224,4 220,2 199,3
Se puede intentar adivinar en clase qué media se ha usado, e
investigar si estos datos entran en lo que es frecuente en la vida real.
Cociente intelectual
A la vista de esta tabla, se puede discutir qué media y
desviación típica se usa y seguir investigando en Internet:
103 87 106 57 100
62 88 81 98 83
102 90 98 103 100
109 76 93 99 100
107 84 75 104 105
91 96 111 121 108
93 89 89 88 92
71 85 92 104 83
82 97 88 91 82
103 85 110 108 94
84 101 94 86 97
105 92 85 120 121










No hay comentarios:
Publicar un comentario