(Con esta entrada particimamos en el VIII Carnaval de Matemáticas, cuyo anfitrión es el blog "Los matemáticos no son gente seria", de nuestro buen amigo Juan Martínez-Tebar)
Un número entero positivo N se llama de Ore o armónico cuando la media armónica de todos sus divisores es un número entero. Por ejemplo, es armónico 140, porque sus 12 divisores son 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70 y 140 y por tanto su media armónica es
Parece muy pesado este cálculo para números grandes, pero existe una simplificación. Para ello basta observar que cada divisor d posee un complementario d’ tales que d.d’=N. Este hecho permite ir sustituyendo cada cociente del tipo 1/d por d’/N, con lo que todos los denominadores resultará iguales a N y se podrán sumar los cocientes con facilidad:
Este procedimiento es fácilmente generalizable: basta multiplicar N por su número de divisores y dividir después entre la suma de los mismos:
Representamos el número de divisores mediante d(N) y su suma por s(N). Basta observar la fórmula para poder interpretarla de otra manera: La media armónica de los divisores equivale al cociente entre el número y la media aritmética de dichos divisores.
Este cambio nos permite calcular la media armónica mediante un sencillo algoritmo: Se encuentran los divisores y se van contando y sumando hasta completar el valor de d(N) y s(N). Si esta media es entera, el número N será armónico.
Incluimos un listado en Basic que lo logra:
Sub armonico
Input n
a=0 Inicia el contador de divisores
b=0 Inicia el sumador de divisores
for j=2 to n/2+1
if esmultiplo(n,j) then
a=a+1 Se ha encontrado un divisor: se aumenta el contador en 1
b=b+j Se aumenta el sumador con el valor del divisor
end if
next j
a=a+2 Se añade 2 para contar también 1 y N
b=b+n+1 Se añaden al sumador 1 y N
m=i*a/b Media armónica
if m=int(m) then msgbox(“Es armónico”) else msgbox(“No es armónico”)
end sub
La siguiente tabla se ha obtenido con la repetición de este algoritmo:
N D S M
6 4 12 2
28 6 56 3
140 12 336 5
270 16 720 6
496 10 992 5
672 24 2016 8
1638 24 4368 9
Los primeros números de Ore son: 1, 6, 28, 140, 270, 496, 672, 1638, 2970, 6200, 8128, 8190,…¿Qué llama la atención en este listado?
Efectivamente, incluye los números perfectos 6, 28, 496, 8128,…y otros más que no lo son. Todo número perfecto se puede demostrar que también es armónico. Esto es interesante, porque si se lograra demostrar la Conjetura de Ore de que no existen armónicos impares, también se habría logrado demostrar que tampoco hay perfectos impares.
En la tabla anterior vemos que los primeros valores de la media armónica son 2, 3, 5, 6, 5, 8, 9…En ellos hay valores repetidos como el 5 y ausentes como el 4. Según un teorema de Kanold, para cada entero positivo s existe solo un número finito de enteros positivos n tales que su media armónica sea s.
Este blog es un complemento natural de mi página http://www.hojamat.es. Por ello, se dedicará a los temas numéricos tratados con Hoja de Cálculo y a la estructura y prestaciones de esta. Su nivel será elemental o medio, y su orientación lúdica e investigadora.
lunes, 15 de noviembre de 2010
domingo, 7 de noviembre de 2010
¿En cuántas sumas de cuadrados? (5 de 5)
Reflexión final
Después de redactar las últimas entradas he recordado que en mis clases de Matemáticas, al explicar los números reales, utilizábamos el Teorema de Pitágoras para representar en la recta real los irracionales cuadráticos. Así situábamos, por ejemplo, la raíz cuadrada de 10 mediante el uso de una recta graduada y un compás:
De igual forma representábamos las raíces cuadradas de 2, 13, 17, etc.
Cosa curiosa: en tantos años nadie me preguntó por la raíz de 7 ¿Cómo se representa en la recta real? ¿Qué le hubieras respondido tú?
Hay dos respuestas al menos: una es acumular triángulos rectángulos a partir de uno de hipotenusa la raíz de 2 adosándole un cateto de medida la unidad, con lo que la hipotenusa equivaldría a la raíz de 3, y así sucesivamente, mediante catetos 1 se irían generando todas la raíces en ora de espiral
Otra es acudir a una diferencia de cuadrados. En la imagen puedes ver la representación de la raíz de 7 tomada como cateto de un triángulo de hipotenusa 4 y el otro cateto 3:
Pero este método tiene un inconveniente, y es que sólo son representables con diferencias de cuadrados los números impares y los múltiplos de 4. Por tanto, el número 14 no se podría construir ni con sumas de cuadrados ni con diferencias.
Hemos descubierto que la descomposición de un número en sumas o bien en diferencias de cuadrados clasifica a los números enteros positivos en cuatro clases. Terminamos este ciclo de entradas como lo comenzamos, con la sección 182 de las Disquisitiones arithmeticae:
Todo número natural según Gauss se puede representar de la siguiente forma:
Donde pi son los factores del tipo 4h+3 y los qi del tipo 4h+1.
Con esa nomenclatura podemos afirmar:
(1) Si a es par y todas la bi pares (contando el 0), N se puede descomponer en suma de dos cuadrados y en diferencia de otros dos. Igualando, N=a2+b2 = m2- n2 y produce de forma indirecta soluciones a la ecuación x2+y2+z2=u2. Sería el caso del número 17 = 42+12= 92-82, que da lugar a la identidad 42+12+82= 92
(2) Si a es impar y todas la bi pares, N equivaldrá a sumas de cuadrados pero no a diferencias. Ocurre esto con el número 10 = 32+12 que no puede escribirse como diferencia de cuadrados a causa de no poder expresarse como dos factores de la misma paridad.
(3) Si a es par y alguna bi impar, admitirá una descomposición en diferencias de cuadrados pero no en sumas (de dos). Así, 15=42-12 y no se puede descomponer en suma por ser del tipo 4h+3.
(4) Por último, no admitirán ninguna descomposición similar los que presenten a impar y alguna bi impar. Es así el número 70 = 2*5*7, que a causa del 2 y el 7 no admitirá ser expresado como suma o diferencia de cuadrados.
Después de redactar las últimas entradas he recordado que en mis clases de Matemáticas, al explicar los números reales, utilizábamos el Teorema de Pitágoras para representar en la recta real los irracionales cuadráticos. Así situábamos, por ejemplo, la raíz cuadrada de 10 mediante el uso de una recta graduada y un compás:
De igual forma representábamos las raíces cuadradas de 2, 13, 17, etc.
Cosa curiosa: en tantos años nadie me preguntó por la raíz de 7 ¿Cómo se representa en la recta real? ¿Qué le hubieras respondido tú?
Hay dos respuestas al menos: una es acumular triángulos rectángulos a partir de uno de hipotenusa la raíz de 2 adosándole un cateto de medida la unidad, con lo que la hipotenusa equivaldría a la raíz de 3, y así sucesivamente, mediante catetos 1 se irían generando todas la raíces en ora de espiral
Otra es acudir a una diferencia de cuadrados. En la imagen puedes ver la representación de la raíz de 7 tomada como cateto de un triángulo de hipotenusa 4 y el otro cateto 3:
Pero este método tiene un inconveniente, y es que sólo son representables con diferencias de cuadrados los números impares y los múltiplos de 4. Por tanto, el número 14 no se podría construir ni con sumas de cuadrados ni con diferencias.
¿Sabrías indicar qué otras dos construcciones geométricas sobre un triángulo rectángulo nos permitirían representar todos los irracionales cuadráticos?
Resumen de la serie de cinco entradas:
Todo número natural según Gauss se puede representar de la siguiente forma:
Donde pi son los factores del tipo 4h+3 y los qi del tipo 4h+1.
Con esa nomenclatura podemos afirmar:
(1) Si a es par y todas la bi pares (contando el 0), N se puede descomponer en suma de dos cuadrados y en diferencia de otros dos. Igualando, N=a2+b2 = m2- n2 y produce de forma indirecta soluciones a la ecuación x2+y2+z2=u2. Sería el caso del número 17 = 42+12= 92-82, que da lugar a la identidad 42+12+82= 92
(2) Si a es impar y todas la bi pares, N equivaldrá a sumas de cuadrados pero no a diferencias. Ocurre esto con el número 10 = 32+12 que no puede escribirse como diferencia de cuadrados a causa de no poder expresarse como dos factores de la misma paridad.
(3) Si a es par y alguna bi impar, admitirá una descomposición en diferencias de cuadrados pero no en sumas (de dos). Así, 15=42-12 y no se puede descomponer en suma por ser del tipo 4h+3.
(4) Por último, no admitirán ninguna descomposición similar los que presenten a impar y alguna bi impar. Es así el número 70 = 2*5*7, que a causa del 2 y el 7 no admitirá ser expresado como suma o diferencia de cuadrados.
Insistimos en la pregunta: ¿Cómo lo podríamos representar en la recta real? Es una cuestión más bien elemental.
jueves, 4 de noviembre de 2010
¿En cuántas sumas de cuadrados? (4 de 5)
Problema del círculo de Gauss
En la anterior entrada nos aparecía el número PI de forma algo sorprendente. En esta veremos que de sorpresa nada. Todo está relacionado, y se basa en la solución del llamado Problema del círculo de Gauss.
No entraremos demasiado en la parte teórica, que podéis consultar en las páginas
o en el Blog “Juan de Mairena”
Lo que presentaremos aquí es su tratamiento con hoja de cálculo, pero con una pequeña introducción.
En las dos entradas anteriores desarrollamos los números enteros positivos como sumas de dos cuadrados de base entera. Estamos en el terreno del Teorema de Pitágoras, y si representamos todas las soluciones para un número N dado como catetos de un triángulo, los puntos representados por ellos se situarán todos en el círculo de radio la raíz cuadrada de N.
Si con una hoja de cálculo creamos una lista de valores X e Y tales que X2+Y2 sea menor o igual que N, según lo explicado, se rellenarán puntos dentro de un círculo, lo que representará perfectamente el círculo de Gauss.
En la imagen puedes ver el gráfico correspondiente a N=22
Para conseguir esta imagen necesitaremos el algoritmo que encuentre todas las soluciones para que X2+Y2 no sobrepase N. Una vez conseguida la lista de soluciones bastará con crear un gráfico del tipo XY para conseguir la aproximación al círculo.
Se puede usar un código en el Basic de OpenOffice.org similar al siguiente (fácilmente adaptable a Excel):
Sub desarrollo(n)
dim i,j,s,t,fi,a,b,x
fi=5
StarDesktop.CurrentComponent.sheets(0).GetCellByPosition(3,fi).value=0
StarDesktop.CurrentComponent.sheets(0).GetCellByPosition(4,fi).value=0
for x=1 to n
i=0
a=sqr(x)
while <=a
j=x-i*i
if j=int(sqr(j))^2 or j=0 then
b=sqr(j)
for s=-1 to 1 step 2
for t=-1 to 1 step 2
fi=fi+1
StarDesktop.CurrentComponent.sheets(0).GetCellByPosition(3,fi).value=i*s
StarDesktop.CurrentComponent.sheets(0).GetCellByPosition(4,fi).value=b*t
next t
next s
end if
i=i+1
wend
next x
End Sub
Puedes descargarte las versiones en Excel 2007 y OpenOffice.org 3 desde la dirección
martes, 2 de noviembre de 2010
¿En cuántas sumas de cuadrados? (3 de 5)
Aparece el número PI
En la entrada anterior se presentaba una fórmula para encontrar el número de descomposiciones distintas en suma de dos cuadrados que puede presentar un número entero positivo. Vimos dos orientaciones: buscar sólo sumandos positivos o admitir también los negativos teniendo en cuenta además el orden.
Para un resultado inesperado que obtendremos más adelante vamos a elegir la segunda opción: encontrar, dado un número entero positivo N, todos los pares x, y de números enteros tales que x2+y2=N. Al número de esos pares lo podemos considerar como función de N, lo que nos permite definir NSC(N)=Número de pares de enteros x, y tales que x2+y2=N
Para implementar esta función en la hoja de cálculo podemos usar un código similar al siguiente (comentarios en cursiva):
Public function nsc(n)
dim i,a,b,ns
if n=0 then
ns=1 Tenemos en cuenta que n puede valer 0
else
ns=0 Se inicia la suma
for i=0 to sqr(n) Busca el primer sumando
a=n-i*I Calcula el segundo sumando
if a=int(sqr(a))^2 then El segundo sumando es un cuadrado
if i*i<=a then Esta línea es para no tener en cuenta el orden de los sumandos
b=sqr(a) Base del segundo cuadrado
if b>0 and i>0 and b<>i then Si ambas bases son positivas y distintas hay 8 posibilidades
ns=ns+8
else Si una es cero o so iguales, sólo hay 4
ns=ns+4
end if
end if
end if
next i
end if
nsc=ns Se recoge el resultado
end function
Esta función, si se declara Public se puede usar en la hoja de cálculo y formar una tabla que compare N con NSC(N):
N NSC(N)
0 1
1 4
2 4
3 0
4 4
5 8
6 0
7 0
8 4
9 4
10 8
Aunque su distribución parece ser muy irregular, nos espera una sorpresa y es que si acumulamos los resultados y vamos calculando el promedio de NSC conforme crece N, este promedio tiene como límite el número PI
En la siguiente tabla puedes observar que para N=20 ya se percibe esta tendencia al límite:
Para N=500 el promedio oscila ya de una forma clara alrededor de 3,14:
y para N=8000 su valor es 3,14213. ¡No nos libramos del número PI!
Puedes descargarte las hojas de cálculo en las que hemos implementado la fórmula de Gauss y la función NSC que cuenta todas las sumas considerando signos y orden en la dirección
http://hojamat.es/blog/sumacuad.zip
En la entrada anterior se presentaba una fórmula para encontrar el número de descomposiciones distintas en suma de dos cuadrados que puede presentar un número entero positivo. Vimos dos orientaciones: buscar sólo sumandos positivos o admitir también los negativos teniendo en cuenta además el orden.
Para un resultado inesperado que obtendremos más adelante vamos a elegir la segunda opción: encontrar, dado un número entero positivo N, todos los pares x, y de números enteros tales que x2+y2=N. Al número de esos pares lo podemos considerar como función de N, lo que nos permite definir NSC(N)=Número de pares de enteros x, y tales que x2+y2=N
Para implementar esta función en la hoja de cálculo podemos usar un código similar al siguiente (comentarios en cursiva):
Public function nsc(n)
dim i,a,b,ns
if n=0 then
ns=1 Tenemos en cuenta que n puede valer 0
else
ns=0 Se inicia la suma
for i=0 to sqr(n) Busca el primer sumando
a=n-i*I Calcula el segundo sumando
if a=int(sqr(a))^2 then El segundo sumando es un cuadrado
if i*i<=a then Esta línea es para no tener en cuenta el orden de los sumandos
b=sqr(a) Base del segundo cuadrado
if b>0 and i>0 and b<>i then Si ambas bases son positivas y distintas hay 8 posibilidades
ns=ns+8
else Si una es cero o so iguales, sólo hay 4
ns=ns+4
end if
end if
end if
next i
end if
nsc=ns Se recoge el resultado
end function
Esta función, si se declara Public se puede usar en la hoja de cálculo y formar una tabla que compare N con NSC(N):
N NSC(N)
0 1
1 4
2 4
3 0
4 4
5 8
6 0
7 0
8 4
9 4
10 8
Aunque su distribución parece ser muy irregular, nos espera una sorpresa y es que si acumulamos los resultados y vamos calculando el promedio de NSC conforme crece N, este promedio tiene como límite el número PI
En la siguiente tabla puedes observar que para N=20 ya se percibe esta tendencia al límite:
Para N=500 el promedio oscila ya de una forma clara alrededor de 3,14:
y para N=8000 su valor es 3,14213. ¡No nos libramos del número PI!
Puedes descargarte las hojas de cálculo en las que hemos implementado la fórmula de Gauss y la función NSC que cuenta todas las sumas considerando signos y orden en la dirección
http://hojamat.es/blog/sumacuad.zip
sábado, 30 de octubre de 2010
¿En cuántas sumas de cuadrados? (2 de 5)
Fórmula de Gauss
Las propiedades vistas en la anterior entrada se resumen en un criterio que no vamos a desarrollar aquí, y es que sólo se pueden descomponer en cuadrados los números en los que los factores primos del tipo 4n+3 figuren en su descomposición con exponente par. Gauss fue más allá en esa sección 182, pues dio una fórmula para contar el número de formas diferentes en las que se descompone un número en suma de dos cuadrados con base no negativa:
donde ES significa “mínimo entero igual o superior” y los factores que le siguen se corresponden con los exponentes de los factores del tipo 4n+1 aumentados en una unidad. La fórmula, como advierte Gauss, sólo es válida si los factores del tipo 4n+3 forman un cuadrado perfecto.
Así, por ejemplo, el número 325=52*13 se deberá descomponer en
N=ES((2+1)(1+1)/2)=ES(3*2/2)=ES(3)=3
En efecto, 325=12 + 182 = 62 + 172 = 102 + 152 (tres formas distintas)
Y el número 6664 sólo de una forma, pues 6664 = 23*72*17 y aplicando la fórmula nos daría
N=ES(1+1)/2 = ES(1)=1, y su descomposición única es 6664=422+702
Actualmente se prefiere considerar todas las sumas de cuadrados posibles, incluyendo bases negativas y teniendo en cuenta el orden. Esto multiplica por 8 el número de soluciones cuando x es distinto de y y ambos son no nulos, y por 4 en caso contrario. Así, el 13 presentaría ocho soluciones:
13= 22+32 = (-2)2+32 = 22+(-3)2 = (-2)2+(-3)2 = 32 +22 =(-3)2 +22 = 32 +(-2)2 = (-3)2 +(-2)2
Y el 16, cuatro: 16 = 42+02 = (-4)2+02 =02 + 42 = 02 + (-4)2
Igualmente, 8 presentaría también 4: 8 = 42+42 = (-4)2+42 =42 + (-4)2 = (-4)2 + (-4)2
¿Por qué complicar así la cuestión? Lo veremos en la siguiente entrada.
martes, 26 de octubre de 2010
¿En cuántas sumas de cuadrados? (1 de 5)
Todo comenzó con Fermat
Hay números que se pueden descomponer en suma de dos cuadrados, pero ¿de cuántas formas? Esta cuestión ha sido ya abordada en otros blogs de Matemáticas, pero aquí añadiremos técnicas y algoritmos de hoja de cálculo.
Para conseguir una respuesta a la pregunta formulada se necesitaron esfuerzos de varios matemáticos, pero todo comenzó con Fermat y su Teorema de Navidad (lo comunicó a Mersenne el 25 de Diciembre de 1640, pero no lo demostró), y que actualmente expresamos así:
Un número primo se puede descomponer en suma de dos cuadrados x2+y2 de números enteros si y sólo si es el número 2 o bien es congruente con 1 módulo 4 (es decir, si es de la forma 4n+1).
El teorema directo es difícil de demostrar, y lo ha sido a lo largo de siglos mediante diversas técnicas (descenso infinito, enteros gausianos y otros), siendo Euler el primero que lo logró. El inverso está a nuestro alcance. Inténtalo:
Gauss, en la sección 182 de sus Disquisitiones arithmeticae destacó que esa descomposición es única, salvo orden y signo. Los dos números x e y han de ser primos entre sí ¿por qué?
De este hecho podemos obtener un criterio marginal: Si un número de la forma 4n+1 no se puede descomponer en dos cuadrados o bien lo puede de más de una forma, no es primo.
Esta propiedad de poder descomponerse en suma de dos cuadrados se mantiene si multiplicamos dos números primos de este tipo, y además se puede duplicar el número de posibles sumas. Así, si 13 = 22+32 y 5 = 22+12, al multiplicarlos obtenemos:
65 = 13*5 = 82+12 = 72+42
Esta propiedad se desprende de la famosa identidad:
(a2+b2 )(c2+d2 )= (ac+bd)2+(ad-bc)2=(ac-bd)2+(ad+bc)2
que nos viene a decir que este producto también es suma de dos cuadrados y además de dos formas distintas (si los sumandos son distintos):
65 = (2*2+3*1)2 +(2*1-3*2)2 = 72+42 (obsérvese que en el cálculo se ha obtenido -4 y no 4)
65 = (2*2-3*1)2 +(2*1+3*2)2 = 82+12
Ocurre lo mismo si se multiplica el número primo por 2 (elemental ¿no?)
En la siguiente entrada veremos una fórmula de Gauss que resume lo expuesto.
Hay números que se pueden descomponer en suma de dos cuadrados, pero ¿de cuántas formas? Esta cuestión ha sido ya abordada en otros blogs de Matemáticas, pero aquí añadiremos técnicas y algoritmos de hoja de cálculo.
Para conseguir una respuesta a la pregunta formulada se necesitaron esfuerzos de varios matemáticos, pero todo comenzó con Fermat y su Teorema de Navidad (lo comunicó a Mersenne el 25 de Diciembre de 1640, pero no lo demostró), y que actualmente expresamos así:
Un número primo se puede descomponer en suma de dos cuadrados x2+y2 de números enteros si y sólo si es el número 2 o bien es congruente con 1 módulo 4 (es decir, si es de la forma 4n+1).
El teorema directo es difícil de demostrar, y lo ha sido a lo largo de siglos mediante diversas técnicas (descenso infinito, enteros gausianos y otros), siendo Euler el primero que lo logró. El inverso está a nuestro alcance. Inténtalo:
Un número primo congruente con 3 módulo 4 no puede descomponerse en suma de dos cuadrados de números enteros.
Gauss, en la sección 182 de sus Disquisitiones arithmeticae destacó que esa descomposición es única, salvo orden y signo. Los dos números x e y han de ser primos entre sí ¿por qué?
De este hecho podemos obtener un criterio marginal: Si un número de la forma 4n+1 no se puede descomponer en dos cuadrados o bien lo puede de más de una forma, no es primo.
Esta propiedad de poder descomponerse en suma de dos cuadrados se mantiene si multiplicamos dos números primos de este tipo, y además se puede duplicar el número de posibles sumas. Así, si 13 = 22+32 y 5 = 22+12, al multiplicarlos obtenemos:
65 = 13*5 = 82+12 = 72+42
Esta propiedad se desprende de la famosa identidad:
(a2+b2 )(c2+d2 )= (ac+bd)2+(ad-bc)2=(ac-bd)2+(ad+bc)2
que nos viene a decir que este producto también es suma de dos cuadrados y además de dos formas distintas (si los sumandos son distintos):
65 = (2*2+3*1)2 +(2*1-3*2)2 = 72+42 (obsérvese que en el cálculo se ha obtenido -4 y no 4)
65 = (2*2-3*1)2 +(2*1+3*2)2 = 82+12
Ocurre lo mismo si se multiplica el número primo por 2 (elemental ¿no?)
En la siguiente entrada veremos una fórmula de Gauss que resume lo expuesto.
miércoles, 20 de octubre de 2010
1, 7, 17, 23, 31, 41, 47, 49, 71, 73, 79, 89, 97, (Segunda parte)
Esta entrada y la anterior constituyen nuestra aportación al VII Carnaval de Matematicas. En esta ocasión, Javier Oribe desde El Máquina de Turing, va a ejercer de anfitrión.
Doblado pitagórico
Si tomamos un segmento de longitud 31 cm. y lo doblamos por cierto punto en forma de ángulo recto, podemos completar un triángulo rectángulo cuya hipotenusa tiene medida entera. No es difícil averiguar por dónde se puede doblar: basta hacerlo con un segmento de medida 7, con lo que el otro trozo mediría 24 y la hipotenusa 25.
Existen otros números con la misma propiedad: 7, descompuesto en 3 y 4, 23, doblado por 8 y 15, y otros muchos.
Te proponemos una búsqueda elemental, mediante razonamiento, hoja de cálculo o navegación por la Red:
Te dejamos este código por si deseas practicar:
(Dado un valor n)
Sub buscar(n)
for i=7 to n
for j=3 to i/2
k=i-j
if escuadrado(k*k+j*j)=1 then
msgbox(i)
msgbox(j)
msgbox(k)
end if
next j
next i
end sub
Si lo resuelves te llevarás una sorpresa: las soluciones son las mismas de la entrada anterior (salvo el número 1)
7, 17, 23, 31, 41, 47, 49, 71, 73, 79, 89, 97, 103, 113, 119, ... y todos sus múltiplos.
Lo puedes ver en esta tabla:
7 3 4
14 6 8
17 5 12
21 9 12
23 8 15
28 12 16
31 7 24
34 10 24
35 15 20
41 20 21
42 18 24
46 16 30
47 12 35
49 9 40
49 21 28
51 15 36
56 24 32
62 14 48 ...
La razón estriba en que ambos problemas están relacionados con la ecuación 2x2-y2=k.
Ahí tienes otro reto por si deseas investigar (esta vez te estamos ayudando poco).
Doblado pitagórico
Si tomamos un segmento de longitud 31 cm. y lo doblamos por cierto punto en forma de ángulo recto, podemos completar un triángulo rectángulo cuya hipotenusa tiene medida entera. No es difícil averiguar por dónde se puede doblar: basta hacerlo con un segmento de medida 7, con lo que el otro trozo mediría 24 y la hipotenusa 25.
Existen otros números con la misma propiedad: 7, descompuesto en 3 y 4, 23, doblado por 8 y 15, y otros muchos.
Te proponemos una búsqueda elemental, mediante razonamiento, hoja de cálculo o navegación por la Red:
Además de 7, 23 o 31, ¿qué otros números tienen la propiedad de engendrar un triángulo rectángulo de medidas enteras con un simple “doblado”?
Te dejamos este código por si deseas practicar:
(Dado un valor n)
Sub buscar(n)
for i=7 to n
for j=3 to i/2
k=i-j
if escuadrado(k*k+j*j)=1 then
msgbox(i)
msgbox(j)
msgbox(k)
end if
next j
next i
end sub
Si lo resuelves te llevarás una sorpresa: las soluciones son las mismas de la entrada anterior (salvo el número 1)
7, 17, 23, 31, 41, 47, 49, 71, 73, 79, 89, 97, 103, 113, 119, ... y todos sus múltiplos.
Lo puedes ver en esta tabla:
7 3 4
14 6 8
17 5 12
21 9 12
23 8 15
28 12 16
31 7 24
34 10 24
35 15 20
41 20 21
42 18 24
46 16 30
47 12 35
49 9 40
49 21 28
51 15 36
56 24 32
62 14 48 ...
La razón estriba en que ambos problemas están relacionados con la ecuación 2x2-y2=k.
Ahí tienes otro reto por si deseas investigar (esta vez te estamos ayudando poco).
martes, 19 de octubre de 2010
1, 7, 17, 23, 31, 41, 47, 49, 71, 73, 79 ... (Primera parte)
Esta entrada y la siguiente (la publicaremos en un par de días) forman nuestra aportación al VII Carnaval de Matematicas. En esta ocasión, Javier Oribe desde El Máquina de Turing, va a ejercer de anfitrión.
1, 7, 17, 23, 31, 41, 47, 49, 71, 73, 79 ...
En una entrada del curso anterior estudiamos las ternas pitagóricas en las que la diferencia entre catetos era igual a 1. Nos podemos plantear también qué números, aparte del 1, pueden ser diferencia entre catetos en esas ternas.
(1) Afirmamos que todo número puede ser diferencia entre catetos en una terna pitagórica. ¿Cómo lo probarías en pocos segundos?
(2) Más difícil es demostrar que todo número es diferencia de catetos de infinitas formas distintas. Para ayudarte puedes demostrar previamente lo siguiente:
Si lo anterior es cierto, reiterando el procedimiento obtendremos infinitas ternas con la misma diferencia (salvo signo u orden). Si la primera es primitiva, todas las demás lo serán ¿Por qué?
Por ejemplo, de u=4, v=3, x=7, y=24, z=25, con diferencia entre catetos igual a 17, podemos engendrar u=11, v=4, x=88, y=105, z=137, con 105-88 = 17 y después u=26, v=11, x=572, y=555 z=797, y así tantas como queramos.
(3) Si sólo admitimos ternas primitivas, no todos los números pueden ser diferencia de catetos. Los únicos posibles son 1, 7, 17, 23, 31, 41, 47, 49, 71, 73, 79, 89, 97, 103, 113, 119, ...
Te proponemos una búsqueda de información para averiguar la razón. Sólo te indicaremos que esos números son los que sólo tienen divisores del tipo 8N+1 o 8N-1.
1, 7, 17, 23, 31, 41, 47, 49, 71, 73, 79 ...
En una entrada del curso anterior estudiamos las ternas pitagóricas en las que la diferencia entre catetos era igual a 1. Nos podemos plantear también qué números, aparte del 1, pueden ser diferencia entre catetos en esas ternas.
(1) Afirmamos que todo número puede ser diferencia entre catetos en una terna pitagórica. ¿Cómo lo probarías en pocos segundos?
(2) Más difícil es demostrar que todo número es diferencia de catetos de infinitas formas distintas. Para ayudarte puedes demostrar previamente lo siguiente:
Si u y v engendran una terna pitagórica mediante las fórmulas 2uv, u2-v2 y u2+v2, los valores 2u+v y v engendran otra terna con la misma diferencia de catetos.
Si lo anterior es cierto, reiterando el procedimiento obtendremos infinitas ternas con la misma diferencia (salvo signo u orden). Si la primera es primitiva, todas las demás lo serán ¿Por qué?
Por ejemplo, de u=4, v=3, x=7, y=24, z=25, con diferencia entre catetos igual a 17, podemos engendrar u=11, v=4, x=88, y=105, z=137, con 105-88 = 17 y después u=26, v=11, x=572, y=555 z=797, y así tantas como queramos.
(3) Si sólo admitimos ternas primitivas, no todos los números pueden ser diferencia de catetos. Los únicos posibles son 1, 7, 17, 23, 31, 41, 47, 49, 71, 73, 79, 89, 97, 103, 113, 119, ...
Te proponemos una búsqueda de información para averiguar la razón. Sólo te indicaremos que esos números son los que sólo tienen divisores del tipo 8N+1 o 8N-1.
lunes, 20 de septiembre de 2010
Cajas y bolas (1)
(Esta entrada es la aportación de este blog la VI Edición del Carnaval de Matemáticas cuyo anfitrión será el Blog de Sangakoo.)
Con esta cuestión iniciamos una serie de entradas (algo que nos llevará algunos meses) a la que titularemos “Cajas y bolas”, porque usaremos esta metodología para repasar conceptos de Combinatoria.
En una entrada anterior proponíamos averiguar de cuántas formas distintas se pueden colorear de negro cincuenta celdas de un tablero de 10 por 10. La solución que proponíamos era 1008913445455641933334812497256.
El problema propuesto equivale a repartir 50 bolas en 100 cajas, de forma que
En la imagen se han repartido 5 bolas en 16 cajas sin que haya ninguna caja con más de una bola. Es fácil ver que el número total de tales repartos es el número combinatorio C16,5 ya que la operación ha consistido en extraer un subconjunto de 5 elementos en un conjunto de 16, lo que constituye la definición de combinaciones sin repetición.
En el problema que nos ocupa de colorear 50 cuadrados negros en un cuadrado de 100 la solución será C100,50 = 100!/(50!*50!) = 1008913445455641933334812497256
Este modelo concreto de cajas y bolas (bolas indistinguibles y no más de una bola por caja) tiene otras muchas aplicaciones:
Loterías
En la Lotería Primitiva de España se extraen seis bolas de un total de 49, que es lo mismo que acomodar seis bolas indistinguibles en 49 cajas numeradas. Quizás no hayas entendido la frase anterior. Repásala. Es como si en el sorteo tuviéramos un tablero de 49 números y marcáramos con una X los premios que han salido. Por tanto, el número de posibilidades es el número combinatorio C49,6 = 13983816
Este mismo modelo concreto de cajas y bolas (más adelante veremos otros) nos servirá, pues, en todos los sorteos que se efectúen mediante extracciones y en los que no influya el orden de los resultados.
Permutaciones con repetición
El ejemplo de las 5 bolas alojadas en 16 cajas también se puede interpretar como que los símbolos VACÍA, LLENA se han permutado de todas las formas posibles, tomando 11 veces VACÍA y 5 veces LLENA, luego podemos usar números combinatorios también en este caso de permutaciones de dos elementos con repetición y número de apariciones fijado para cada uno.
En el ejemplo del tablero de 10 por 10, serían permutaciones de 50 cuadros negros y 50 blancos. Según lo que sabemos de Combinatoria, su número sería 100!/(50!*50!), que coincide con la solución propuesta del número combinatorio C100,50.
Con esta cuestión iniciamos una serie de entradas (algo que nos llevará algunos meses) a la que titularemos “Cajas y bolas”, porque usaremos esta metodología para repasar conceptos de Combinatoria.
En una entrada anterior proponíamos averiguar de cuántas formas distintas se pueden colorear de negro cincuenta celdas de un tablero de 10 por 10. La solución que proponíamos era 1008913445455641933334812497256.
El problema propuesto equivale a repartir 50 bolas en 100 cajas, de forma que
- No puede haber más de una bola por caja.
- Se considera que las cajas se distinguen unas de otras, pero que las bolas son indistinguibles.
En la imagen se han repartido 5 bolas en 16 cajas sin que haya ninguna caja con más de una bola. Es fácil ver que el número total de tales repartos es el número combinatorio C16,5 ya que la operación ha consistido en extraer un subconjunto de 5 elementos en un conjunto de 16, lo que constituye la definición de combinaciones sin repetición.
En el problema que nos ocupa de colorear 50 cuadrados negros en un cuadrado de 100 la solución será C100,50 = 100!/(50!*50!) = 1008913445455641933334812497256
Este modelo concreto de cajas y bolas (bolas indistinguibles y no más de una bola por caja) tiene otras muchas aplicaciones:
Loterías
En la Lotería Primitiva de España se extraen seis bolas de un total de 49, que es lo mismo que acomodar seis bolas indistinguibles en 49 cajas numeradas. Quizás no hayas entendido la frase anterior. Repásala. Es como si en el sorteo tuviéramos un tablero de 49 números y marcáramos con una X los premios que han salido. Por tanto, el número de posibilidades es el número combinatorio C49,6 = 13983816
Este mismo modelo concreto de cajas y bolas (más adelante veremos otros) nos servirá, pues, en todos los sorteos que se efectúen mediante extracciones y en los que no influya el orden de los resultados.
Permutaciones con repetición
El ejemplo de las 5 bolas alojadas en 16 cajas también se puede interpretar como que los símbolos VACÍA, LLENA se han permutado de todas las formas posibles, tomando 11 veces VACÍA y 5 veces LLENA, luego podemos usar números combinatorios también en este caso de permutaciones de dos elementos con repetición y número de apariciones fijado para cada uno.
En el ejemplo del tablero de 10 por 10, serían permutaciones de 50 cuadros negros y 50 blancos. Según lo que sabemos de Combinatoria, su número sería 100!/(50!*50!), que coincide con la solución propuesta del número combinatorio C100,50.
¿Qué cambiaría si las bolas fueran distinguibles?
lunes, 14 de junio de 2010
¿Eres un poligonal?
(Esta entrada constituye la participación de este blog en el V Carnaval de Matemáticas)
Si reuniéramos en una sola lista los números triangulares, cuadrangulares, pentagonales, etc. ¿llenarían todo el conjunto de los números naturales?
Si reuniéramos en una sola lista los números triangulares, cuadrangulares, pentagonales, etc. ¿llenarían todo el conjunto de los números naturales?
Podemos llamar orden n del número poligonal al número de unidades incluidas en uno de sus lados, y tipo k, al número de lados. Evidentemente, si consideramos los poligonales de orden 1, cualquier número N se puede representar como un polígono de N lados, luego la respuesta es afirmativa.
El problema es más interesante si sólo estudiamos números poligonales de al menos orden 2.
Existen números que son triangulares, como el 10, pentagonales, como el 22, o incluso algunos, como el 28, que son triangulares y hexagonales simultáneamente, como puedes observar en la imagen:
¿Existirán números que sólo puedan considerarse como poligonales de grado uno y no admitan otras representaciones poligonales?
Dado un número cualquiera, como 2011 (el 2010 ya vimos que era poligonal de orden 21), sería interesante averiguar qué representaciones admite como número poligonal. Se puede abordar el problema desde varios puntos de vista. Veamos el más sencillo:
Generación mediante triangulares
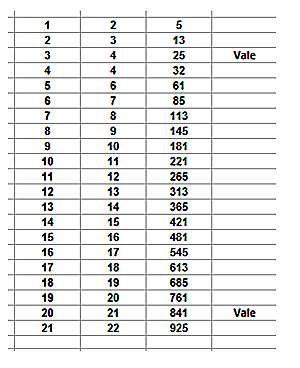
Todo número poligonal de orden n y tipo k se puede generar mediante esta fórmula:
Pn,k = n + (k-2)Tn-1
siendo Tn-1 el número triangular de orden n-1.
No es difícil justificar esta fórmula La simple visión de la siguiente imagen te permite comprenderla. Las unidades azules representan a n, y las de los otros tres colores a los números triangulares que terminan de engendrar el pentagonal:
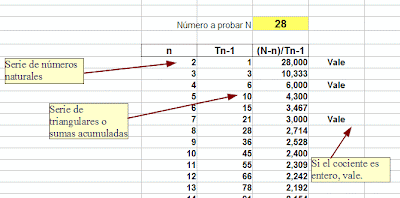
Así que para saber si un número es n-gonal bastará restarle el valor de n y después averiguar si la diferencia contiene a Tn-1 un número entero de veces.
En una hoja de cálculo se pueden organizar tres columnas: La primera con los números naturales n, la segunda con sus sumas acumuladas, que serían los números triangulares T, y en la tercera el cociente (N-n)/T. Si este cociente es entero, hemos descubierto que el número probado es n-gonal.
En la imagen tienes el proceso para descubrir que el número 28 es 28-gonal, hexagonal y triangular. como ya sabíamos.
También podemos comprobar que hay números, como el 2011, que sólo admiten formar un polígono de grado 1 y tipo 2011. Sin embargo, el 2016 admite seis representaciones, con tipos 2016, 673, 136, 24, 6 y 3.
Generación mediante fórmula
De la generación de números poligonales a partir de triangulares se puede deducir la popular fórmula
Pn,k=n(n(k-2)-(k-4))/2
Si la consideramos como ecuación de segundo grado en n, se puede exigir que su discriminante sea cuadrado perfecto, es decir:
D=(k-4)2+8Pn,k(k-2)=M2
Esto nos da otro procedimiento: Recorremos valores de k y observamos cuáles producen cuadrados perfectos y después si el valor de n es entero. En la imagen puedes observar cómo se organiza la búsqueda en hoja de cálculo
lunes, 12 de abril de 2010
Factorización de Fermat a paso de tortuga
(Esta entrada constituye la participación de este blog en el Tercer Carnaval de Matemáticas)
La factorización de Fermat siempre se ha presentado como una técnica para representar un número impar como producto de dos de sus factores sin usar la lista de números primos. No es el único algoritmo de factorización con esa propiedad. Si extraemos progresivamente el factor más pequeño (mayor que 1) de N aseguraremos que hemos encontrado un número primo sin tener que memorizar la lista de primos (busca la herramienta factores en la dirección http:/www.hojamat.es/sindecimales/divisibilidad/herramientas/herrdiv.htm y estudia su funcionamiento).
En efecto, la factorización de Fermat no se basa en los factores primos, sino en representar un número impar N como una diferencia de dos cuadrados y después expresar la misma como el producto de una suma por una diferencia, con lo que se logra la factorización:
N=y2- x2=(x+y)(y-x)
En el caso impar esta operación siempre es posible, porque N=(N+1)2/4-(N-1)2/4, que da lugar a la factorización N=N.1
Desde el punto de vista algorítmico, la búsqueda de los valores de x e y adecuados presenta también otra originalidad, y es que se puede organizar de forma bastante eficiente sólo con sumas y comparaciones. En realidad, todos los algoritmos se pueden organizar así, y en caso último mediante la máquina de Turing, pero tampoco hay que llegar tan lejos. En la búsqueda de la factorización de Fermat se logran resultados bastante aceptables. Es una tortuga, pero algo veloz.
La creación del algoritmo se basa en estos hechos que te pedimos intentes justificar:
(1) El valor de y, y por tanto el de x, están acotados, y su cota no está excesivamente alejada de n ¿Cuál es y cómo se demuestra?
(2) Para demostrar que un número es cuadrado perfecto, no es necesario dividir ni extraer la raíz cuadrada ¿Cómo se hace?
(3) En realidad, la factorización de Fermat consiste en darle al número impar la figura de escuadra simétrica (gnomon) de varias formas posibles. Observando la imagen puedes resolver las dos primeras cuestiones.
(4) Podemos encontrar la raíz cuadrada entera de un número haciendo crecer de forma simultánea dos sucesiones, una linealmente y otra de forma cuadrática. Esto parece obvio, pero ¿cómo se organiza?
Podemos representar el algoritmo como una carrera, liebre y tortuga, entre a=x2 y b=y2, en la que la tortuga sale con ventaja porque se suma al número N, ya que ha de ser y2=x2+N. Todo esto suena a metáfora, pero funciona.
Daremos a continuación un desarrollo en el que se ocultarán algunos detalles para hacer pensar un poco a quien lo siga.
Tomamos tres variables, y, a, i
Las iniciamos a y=1; a=1; i=1
Mientras a no sobrepase a N hacemos crecer estas variables así: y=y+1; i=i+2; a=a+i
con lo que lograremos el primer cuadrado que es mayor o igual que N
Sólo hemos usado sumas y una comparación. Razona por qué se da este resultado.
Una vez obtenido y2 iniciamos el crecimiento de la misma forma para x2
x=1; b=1; j=1
Mientras N+b no sobrepase a y2, hacemos crecer las variables:
x=x+1; j=j+2; b=b+j
para formar el cuadrado x2
Si ocurre que N+b=a hemos conseguido una factorización, pues N=y2-x2
Ya sólo queda hacer crecer a y b de la misma forma y comprobar si se da la igualdad N+b=a en más ocasiones, y así hasta la cota.
No hemos querido usar el lenguaje algorítmico, y se han ocultado algunos detalles, como qué hacer si N es un cuadrado perfecto. Lo importante de lo explicado es que sólo hemos sumado y comparado. No se ha recurrido a multiplicar, dividir o extraer la raíz cuadrada.
Puedes estudiar más a fondo el algoritmo en las hojas de cálculo factorfermat.ods y factorfermat.xls, contenidas en el archivo http:/www.hojamat.es/blog/factorfermat.zip
Si recorres el código de la macro usada, sólo verás operaciones de sumar. El proceso no es un prodigio de velocidad, pero esto es un divertimiento. La idea de hoy no era correr, sino demostrar una posibilidad. Tampoco corrió Fermat y hay que ver lo que logró.
La factorización de Fermat siempre se ha presentado como una técnica para representar un número impar como producto de dos de sus factores sin usar la lista de números primos. No es el único algoritmo de factorización con esa propiedad. Si extraemos progresivamente el factor más pequeño (mayor que 1) de N aseguraremos que hemos encontrado un número primo sin tener que memorizar la lista de primos (busca la herramienta factores en la dirección http:/www.hojamat.es/sindecimales/divisibilidad/herramientas/herrdiv.htm y estudia su funcionamiento).
En efecto, la factorización de Fermat no se basa en los factores primos, sino en representar un número impar N como una diferencia de dos cuadrados y después expresar la misma como el producto de una suma por una diferencia, con lo que se logra la factorización:
N=y2- x2=(x+y)(y-x)
En el caso impar esta operación siempre es posible, porque N=(N+1)2/4-(N-1)2/4, que da lugar a la factorización N=N.1
Desde el punto de vista algorítmico, la búsqueda de los valores de x e y adecuados presenta también otra originalidad, y es que se puede organizar de forma bastante eficiente sólo con sumas y comparaciones. En realidad, todos los algoritmos se pueden organizar así, y en caso último mediante la máquina de Turing, pero tampoco hay que llegar tan lejos. En la búsqueda de la factorización de Fermat se logran resultados bastante aceptables. Es una tortuga, pero algo veloz.
La creación del algoritmo se basa en estos hechos que te pedimos intentes justificar:
(1) El valor de y, y por tanto el de x, están acotados, y su cota no está excesivamente alejada de n ¿Cuál es y cómo se demuestra?
(2) Para demostrar que un número es cuadrado perfecto, no es necesario dividir ni extraer la raíz cuadrada ¿Cómo se hace?
(3) En realidad, la factorización de Fermat consiste en darle al número impar la figura de escuadra simétrica (gnomon) de varias formas posibles. Observando la imagen puedes resolver las dos primeras cuestiones.
(4) Podemos encontrar la raíz cuadrada entera de un número haciendo crecer de forma simultánea dos sucesiones, una linealmente y otra de forma cuadrática. Esto parece obvio, pero ¿cómo se organiza?
Podemos representar el algoritmo como una carrera, liebre y tortuga, entre a=x2 y b=y2, en la que la tortuga sale con ventaja porque se suma al número N, ya que ha de ser y2=x2+N. Todo esto suena a metáfora, pero funciona.
Daremos a continuación un desarrollo en el que se ocultarán algunos detalles para hacer pensar un poco a quien lo siga.
Obtención de un primer valor de a=y2
Las iniciamos a y=1; a=1; i=1
Mientras a no sobrepase a N hacemos crecer estas variables así: y=y+1; i=i+2; a=a+i
con lo que lograremos el primer cuadrado que es mayor o igual que N
Sólo hemos usado sumas y una comparación. Razona por qué se da este resultado.
Obtención de valores adecuados de a=y2 y de b=x2
Una vez obtenido y2 iniciamos el crecimiento de la misma forma para x2
x=1; b=1; j=1
Mientras N+b no sobrepase a y2, hacemos crecer las variables:
x=x+1; j=j+2; b=b+j
para formar el cuadrado x2
Si ocurre que N+b=a hemos conseguido una factorización, pues N=y2-x2
Obtenemos todas las coincidencias
Ya sólo queda hacer crecer a y b de la misma forma y comprobar si se da la igualdad N+b=a en más ocasiones, y así hasta la cota.
No hemos querido usar el lenguaje algorítmico, y se han ocultado algunos detalles, como qué hacer si N es un cuadrado perfecto. Lo importante de lo explicado es que sólo hemos sumado y comparado. No se ha recurrido a multiplicar, dividir o extraer la raíz cuadrada.
Puedes estudiar más a fondo el algoritmo en las hojas de cálculo factorfermat.ods y factorfermat.xls, contenidas en el archivo http:/www.hojamat.es/blog/factorfermat.zip
Si recorres el código de la macro usada, sólo verás operaciones de sumar. El proceso no es un prodigio de velocidad, pero esto es un divertimiento. La idea de hoy no era correr, sino demostrar una posibilidad. Tampoco corrió Fermat y hay que ver lo que logró.
martes, 30 de marzo de 2010
Oblongos y pitagóricos (3)
La ecuación x2+(x+1)2 =y2 se puede desarrollar de esta forma: x2+(x+1)2 =y2; 2x2+2x+1=y2; (2x+1)2 + 1 = 2y2 ; (2x+1)2 - 2y2 = -1, por lo que llamando z=2x+1 desembocamos en una ecuación de Pell con segundo miembro igual a -1
z2-2y2 = -1
Utilizamos las hojas de cálculo que presentamos en una entrada anterior
http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/pell.ods para Calc
http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/pell.xls para Excel
con el resultado que indica la imagen:

en la que valdrán las soluciones correspondientes a -1
Z=1; Y=1; Imposible, pues X sería negativo
Z=7; Y=5 X=3; X+1=4; Y=5
Z=41; Y=29 X=20; X+1=21;Y=29
Z=239;Y=169 X=119; X+1=120; Y=169
Z=1393;Y=985 X=696;X+1=697; Y=985
que coinciden con las propuestas en la anterior entrada dedicada a este tema.
Este método tiene el inconveniente de que depende de la precisión que tenga la hoja de cálculo en los datos con coma flotante, lo que hará que se rompa en algún momento la periodicidad de los cocientes, en este caso el 2. Por ello se puede completar con una fórmula recursiva que obtenga soluciones exactas conociendo las primeras.
En este ejemplo cada elemento de las distintas celdas cumple la fórmula
an+2 = 2an+1 + an
pero como las soluciones aparecen de forma alternada, deberemos reiterar dos veces, y nos quedará:
an+4 = 2an+3 + an+2 = 2(2an+2 + an+1)+ 2an+1 + an = 4an+2 + 4an+1+ an = 6an+2 - an
Con esta fórmula recursiva se van obteniendo las soluciones sin errores a partir de las dos primeras:
Z0 = 1; Z2 = 7; Z2 = 6*7-1 = 41; Z2 = 6*41-7 =239; …
Y0 = 1; Y2 = 5; Y4 = 6*5-1 = 29; Y6 = 6*29-5 =169; …
Pero no olvidemos que Z es una variable auxiliar Z=2X+1 y que después debemos despejar X
La siguiente lista de ternas, que coincide con la primera que propuso Girard, se ha obtenido mediante esta técnica
1 0 1
5 3 4
29 20 21
169 119 120
985 696 697
5741 4059 4060
33461 23660 23661
195025 137903 137904
1136689 803760 803761
6625109 4684659 4684660
38613965 27304196 27304197
225058681 159140519 159140520
1311738121 927538920 927538921
7645370045 5406093003 5406093004
44560482149 31509019100 31509019101
259717522849 183648021599 183648021600
1513744654945 1070379110496 1070379110497
8822750406821 6238626641379 6238626641380
51422757785981 36361380737780 36361380737781
299713796309065 211929657785303 211929657785304
Un reto: Fermat propuso una fórmula de recurrencia para generar ternas de este tipo a partir de otras similares. Dada la terna (x,x+1,y), se puede generar otra similar (x’,x’+1,y’)
mediante las fórmulas x’=2x+3y+1 y’=4x+3y+2.
¿Sabrías demostrarlo? ¿Engendra todas las ternas posibles a partir de 3,4,5?
z2-2y2 = -1
Utilizamos las hojas de cálculo que presentamos en una entrada anterior
http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/pell.ods para Calc
http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/pell.xls para Excel
con el resultado que indica la imagen:

en la que valdrán las soluciones correspondientes a -1
Z=1; Y=1; Imposible, pues X sería negativo
Z=7; Y=5 X=3; X+1=4; Y=5
Z=41; Y=29 X=20; X+1=21;Y=29
Z=239;Y=169 X=119; X+1=120; Y=169
Z=1393;Y=985 X=696;X+1=697; Y=985
que coinciden con las propuestas en la anterior entrada dedicada a este tema.
Este método tiene el inconveniente de que depende de la precisión que tenga la hoja de cálculo en los datos con coma flotante, lo que hará que se rompa en algún momento la periodicidad de los cocientes, en este caso el 2. Por ello se puede completar con una fórmula recursiva que obtenga soluciones exactas conociendo las primeras.
En este ejemplo cada elemento de las distintas celdas cumple la fórmula
an+2 = 2an+1 + an
pero como las soluciones aparecen de forma alternada, deberemos reiterar dos veces, y nos quedará:
an+4 = 2an+3 + an+2 = 2(2an+2 + an+1)+ 2an+1 + an = 4an+2 + 4an+1+ an = 6an+2 - an
Con esta fórmula recursiva se van obteniendo las soluciones sin errores a partir de las dos primeras:
Z0 = 1; Z2 = 7; Z2 = 6*7-1 = 41; Z2 = 6*41-7 =239; …
Y0 = 1; Y2 = 5; Y4 = 6*5-1 = 29; Y6 = 6*29-5 =169; …
Pero no olvidemos que Z es una variable auxiliar Z=2X+1 y que después debemos despejar X
La siguiente lista de ternas, que coincide con la primera que propuso Girard, se ha obtenido mediante esta técnica
1 0 1
5 3 4
29 20 21
169 119 120
985 696 697
5741 4059 4060
33461 23660 23661
195025 137903 137904
1136689 803760 803761
6625109 4684659 4684660
38613965 27304196 27304197
225058681 159140519 159140520
1311738121 927538920 927538921
7645370045 5406093003 5406093004
44560482149 31509019100 31509019101
259717522849 183648021599 183648021600
1513744654945 1070379110496 1070379110497
8822750406821 6238626641379 6238626641380
51422757785981 36361380737780 36361380737781
299713796309065 211929657785303 211929657785304
Un reto: Fermat propuso una fórmula de recurrencia para generar ternas de este tipo a partir de otras similares. Dada la terna (x,x+1,y), se puede generar otra similar (x’,x’+1,y’)
mediante las fórmulas x’=2x+3y+1 y’=4x+3y+2.
¿Sabrías demostrarlo? ¿Engendra todas las ternas posibles a partir de 3,4,5?
viernes, 26 de marzo de 2010
Oblongos y pitagóricos (2)
¿Cómo organizar una búsqueda de soluciones para x2+(x+1)2 =y2 con hoja de cálculo?
Si no lo pensaste al leer la entrada anterior, ahí van dos propuestas:
Elemental
Rellena una columna con los primeros números naturales consecutivos, y en la columna de su derecha auméntalos en una unidad. Supongamos que has comenzado en las celdas B4 y C4 respectivamente. En ese caso puedes rellenar la celda D4 con la fórmula B4^2+C4^2, y en la E4 una condición que nos devuelva la palabra “Vale” si es cuadrado perfecto:
SI(D4=(ENTERO(RAÍZ(D4))^2; “Vale”;””).
Si usas Excel suprime la tilde de la palabra RAIZ. De esta forma descubriremos las soluciones, con algo de paciencia, tiempo y muchas filas de hoja de cálculo:
Con Basic
La misma idea de construir una lista para X, otra para X+1 y una tercera en la que buscamos los cuadrados perfectos se puede construir en Basic. X lo almacenamos en la variable i, X+1 en la j, y la hipotenusa en k. Una sentencia IF nos presenta las soluciones en las que k es un entero.
Con este código se buscan las soluciones para números inferiores a 1000000.
Sub busquedas
Dim i,j,k
for i=1 to 1000000
j=i+1
k=i^2+j^2
if k=Int(sqr(k))^2 then
msgbox(i)
msgbox(j)
msgbox(sqr(k))
end if
next i
End Sub
Otro día nos pondremos más serios e intentaremos un estudio algebraico. Si te quieres adelantar…
Si no lo pensaste al leer la entrada anterior, ahí van dos propuestas:
Elemental
Rellena una columna con los primeros números naturales consecutivos, y en la columna de su derecha auméntalos en una unidad. Supongamos que has comenzado en las celdas B4 y C4 respectivamente. En ese caso puedes rellenar la celda D4 con la fórmula B4^2+C4^2, y en la E4 una condición que nos devuelva la palabra “Vale” si es cuadrado perfecto:
SI(D4=(ENTERO(RAÍZ(D4))^2; “Vale”;””).
Si usas Excel suprime la tilde de la palabra RAIZ. De esta forma descubriremos las soluciones, con algo de paciencia, tiempo y muchas filas de hoja de cálculo:

Con Basic
La misma idea de construir una lista para X, otra para X+1 y una tercera en la que buscamos los cuadrados perfectos se puede construir en Basic. X lo almacenamos en la variable i, X+1 en la j, y la hipotenusa en k. Una sentencia IF nos presenta las soluciones en las que k es un entero.
Con este código se buscan las soluciones para números inferiores a 1000000.
Sub busquedas
Dim i,j,k
for i=1 to 1000000
j=i+1
k=i^2+j^2
if k=Int(sqr(k))^2 then
msgbox(i)
msgbox(j)
msgbox(sqr(k))
end if
next i
End Sub
Otro día nos pondremos más serios e intentaremos un estudio algebraico. Si te quieres adelantar…
lunes, 22 de marzo de 2010
Oblongos y pitagóricos (1)
Una cuestión que ha dado juego desde los tiempos de Girard y Fermat y que permite recorrer alternativas de cálculo es la siguiente:
De todos los triángulos rectángulos de lados enteros ¿Cuáles cumplen que la diferencia entre los catetos es la unidad?
El primero que la cumple es el popular de lados 3, 4 y 5, pues la diferencia entre 3 y 4 es una unidad. ¿Habrá más? ¿Cómo abordamos el cálculo?
Casi todos los caminos nos llevan a una ecuación diofántica de segundo grado, pero hay que ver cuál y cómo resolverla. También podemos intentar una búsqueda con hoja de cálculo.
Quizás fuera prudente comenzar con esta última posibilidad. Si lo intentas descubrirás al menos estas soluciones:
3, 4 y 5
20, 21 y 29
119, 120 y 169
696, 697 y 985
4059, 4060 y 5741
23660,23661 y 33461
137903, 137904 y 195025
En la siguiente entrada propondremos la organización de una posible búsqueda por si no se te ocurre nada.
De todos los triángulos rectángulos de lados enteros ¿Cuáles cumplen que la diferencia entre los catetos es la unidad?
El primero que la cumple es el popular de lados 3, 4 y 5, pues la diferencia entre 3 y 4 es una unidad. ¿Habrá más? ¿Cómo abordamos el cálculo?
Casi todos los caminos nos llevan a una ecuación diofántica de segundo grado, pero hay que ver cuál y cómo resolverla. También podemos intentar una búsqueda con hoja de cálculo.
Quizás fuera prudente comenzar con esta última posibilidad. Si lo intentas descubrirás al menos estas soluciones:
3, 4 y 5
20, 21 y 29
119, 120 y 169
696, 697 y 985
4059, 4060 y 5741
23660,23661 y 33461
137903, 137904 y 195025
En la siguiente entrada propondremos la organización de una posible búsqueda por si no se te ocurre nada.
domingo, 21 de febrero de 2010
Ecuación de Pell
Se llama ecuación de Pell (por error, porque Pell no la estudió) a la ecuación diofántica cuadrática X2 - DY2 = 1, con X e Y variables enteras y D número entero positivo no cuadrado perfecto.
Existe una variante con el segundo miembro -1 que se resuelve de forma similar, con algunas restricciones, y también se consideran los casos en los que se trate de cualquier número entero.
En su resolución hay que distinguir dos problemas:
Una primera solución no es difícil de encontrar en general.
(a) Puedes acudir a un simple tanteo entre cuadrados perfectos. Por ejemplo, una solución de X2 - 6Y2 = 1 es X0=5 Y0=2. Con una hoja de cálculo no es tarea muy complicada.
(b) Las fracciones continuas también son útiles en la resolución de esta ecuación. Basta para ello desarrollar la raíz cuadrada de D mediante ellas y, según vimos en una entrada anterior, aprovechar la periodicidad del desarrollo. En el caso de la ecuación de Pell basta tomar las reducidas anteriores a la finalización del primer periodo.
En la imagen observarás que la solución X0=5,Y0=2 aparece antes del final del primer periodo [2,4] en el desarrollo por fracciones continuas. Después siguen otras: X=49, Y=20, X=485, Y=198, etc.
En nuestro modelo de hoja de cálculo que recomendamos más abajo basta escribir el valor de D y el segundo miembro +1 ó -1 y la hoja se encarga de desarrollar la raíz cuadrada de D mediante fracciones continuas:
(c) En el documento recomendado al final de esta entrada puedes estudiar estos y otros métodos muy útiles.
Según la teoría del anillo Q(R), siendo R la raíz cuadrada de D (no lo desarrollaremos aquí), las primeras soluciones, escritas como
constituyen una unidad del anillo, y también lo serán todas sus potencias, por lo que las siguientes soluciones provendrán de los desarrollos de las expresiones
agrupando después los términos que no contienen el radical como valor de Y y los que sí lo contienen como valor de X. Este método puede ser fatigoso, por lo que es mejor ir obteniendo las distintas soluciones por recurrencia. En efecto, de la anterior consideración se deduce que
O bien, separando términos:
Estas son las fórmulas que hemos usado en la hoja de cálculo.
Puedes consultar la búsqueda de la primera solución por fracciones continuas y la recurrencia para las siguientes en las hojas de cálculo
http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/pell.ods para Calc
http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/pell.xls para Excel
Por ejemplo, intenta resolver esta cuestión: ¿Qué cuadrado perfecto de diez cifras, al quitarle una unidad se puede descomponer en cinco cuadrados perfectos idénticos?
Existe una variante con el segundo miembro -1 que se resuelve de forma similar, con algunas restricciones, y también se consideran los casos en los que se trate de cualquier número entero.
En su resolución hay que distinguir dos problemas:
Primera solución
Una primera solución no es difícil de encontrar en general.
(a) Puedes acudir a un simple tanteo entre cuadrados perfectos. Por ejemplo, una solución de X2 - 6Y2 = 1 es X0=5 Y0=2. Con una hoja de cálculo no es tarea muy complicada.
(b) Las fracciones continuas también son útiles en la resolución de esta ecuación. Basta para ello desarrollar la raíz cuadrada de D mediante ellas y, según vimos en una entrada anterior, aprovechar la periodicidad del desarrollo. En el caso de la ecuación de Pell basta tomar las reducidas anteriores a la finalización del primer periodo.
En la imagen observarás que la solución X0=5,Y0=2 aparece antes del final del primer periodo [2,4] en el desarrollo por fracciones continuas. Después siguen otras: X=49, Y=20, X=485, Y=198, etc.
En nuestro modelo de hoja de cálculo que recomendamos más abajo basta escribir el valor de D y el segundo miembro +1 ó -1 y la hoja se encarga de desarrollar la raíz cuadrada de D mediante fracciones continuas:
(c) En el documento recomendado al final de esta entrada puedes estudiar estos y otros métodos muy útiles.
Siguientes soluciones
Según la teoría del anillo Q(R), siendo R la raíz cuadrada de D (no lo desarrollaremos aquí), las primeras soluciones, escritas como
constituyen una unidad del anillo, y también lo serán todas sus potencias, por lo que las siguientes soluciones provendrán de los desarrollos de las expresiones
agrupando después los términos que no contienen el radical como valor de Y y los que sí lo contienen como valor de X. Este método puede ser fatigoso, por lo que es mejor ir obteniendo las distintas soluciones por recurrencia. En efecto, de la anterior consideración se deduce que
O bien, separando términos:
Estas son las fórmulas que hemos usado en la hoja de cálculo.
Puedes consultar la búsqueda de la primera solución por fracciones continuas y la recurrencia para las siguientes en las hojas de cálculo
http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/pell.ods para Calc
http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/pell.xls para Excel
Por ejemplo, intenta resolver esta cuestión: ¿Qué cuadrado perfecto de diez cifras, al quitarle una unidad se puede descomponer en cinco cuadrados perfectos idénticos?
Nuestro colaborador Rafael Parra Machío nos ha facilitado un documento muy interesante sobre la ecuación de Pell, en el que podrás consultar otros métodos de resolución, como el que usa aritmética modular, y también algunos detalles históricos y teóricos que no hemos incluido aquí.
Lo puedes descargar desde la dirección http://www.hojamat.es/parra/pell.pdf
martes, 16 de febrero de 2010
Aproximación diofántica (2)
Cualquier número expresado en forma decimal puede representarse mediante una fracción continua. Si el número es racional, ésta será finita, pero si es irracional no podrá serlo, y tendríamos que prolongar el desarrollo de la fracción continua hasta el infinito. En los siguientes párrafos veremos cómo.
Un caso muy interesante es el de los irracionales cuadráticos, que, como demostró Lagrange, presentan desarrollos periódicos.
¿Cómo desarrollar un decimal cualquiera en fracción continua exacta (caso racional) o aproximada (si es irracional)?
La idea es: separamos la parte entera y la parte decimal del número N=e+d, y la decimal la expresamos así: N=e+1/(1/d). Volvemos a separar parte entera y decimal de 1/d y reiteramos, con lo que irán apareciendo los cocientes enteros de una fracción continua. Además de esta idea, existen otros procedimientos con más contenido teórico que no desarrollaremos aquí.
Probamos con la raíz cuadrada de 3. Los cálculos serían:
1,73205080757 = 1+ (1/(1/1,73205080757) =
1+ 1/1,36602540378 = 1+ 1/(1+1/2,73205080760) =
1+1/(1+1/(2+1/1,36602540378) = ….
Al salir este último número se descubre la periodicidad, luego 1,73205080757 equivale a la fracción continua
[1,1,2,1,2,1,2,….] que es periódica por tratarse de un irracional cuadrático.
A continuación destacamos algunos desarrollos importantes:

Números metálicos
Número de oro

Número de plata

Número de bronce

Las hojas de cálculo
http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/fraccont.xls
http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/fraccont.ods
automatizan el proceso. Si las descargas recuerda que están compuestas de dos hojas, una para números fraccionarios y otra para racionales. Si en la primera escribes =RAIZ(3) (En Calc con tilde: RAÍZ) obtendrás las aproximaciones (leyendo las reducidas) a la raíz cuadrada de 3.
El carácter aproximado de los cálculos produce que se rompan las posibles periodicidades después de muchos pasos.
Un caso muy interesante es el de los irracionales cuadráticos, que, como demostró Lagrange, presentan desarrollos periódicos.
¿Cómo desarrollar un decimal cualquiera en fracción continua exacta (caso racional) o aproximada (si es irracional)?
La idea es: separamos la parte entera y la parte decimal del número N=e+d, y la decimal la expresamos así: N=e+1/(1/d). Volvemos a separar parte entera y decimal de 1/d y reiteramos, con lo que irán apareciendo los cocientes enteros de una fracción continua. Además de esta idea, existen otros procedimientos con más contenido teórico que no desarrollaremos aquí.
Probamos con la raíz cuadrada de 3. Los cálculos serían:
1,73205080757 = 1+ (1/(1/1,73205080757) =
1+ 1/1,36602540378 = 1+ 1/(1+1/2,73205080760) =
1+1/(1+1/(2+1/1,36602540378) = ….
Al salir este último número se descubre la periodicidad, luego 1,73205080757 equivale a la fracción continua
[1,1,2,1,2,1,2,….] que es periódica por tratarse de un irracional cuadrático.
A continuación destacamos algunos desarrollos importantes:

Números metálicos
Número de oro

Número de plata

Número de bronce

Las hojas de cálculo
http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/fraccont.xls
http://www.hojamat.es/sindecimales/aritmetica/herramientas/hoja/fraccont.ods
automatizan el proceso. Si las descargas recuerda que están compuestas de dos hojas, una para números fraccionarios y otra para racionales. Si en la primera escribes =RAIZ(3) (En Calc con tilde: RAÍZ) obtendrás las aproximaciones (leyendo las reducidas) a la raíz cuadrada de 3.
El carácter aproximado de los cálculos produce que se rompan las posibles periodicidades después de muchos pasos.
domingo, 14 de febrero de 2010
Aproximación diofántica
¿Sabías que la fracción 3650401/2107560 es una muy buena aproximación de la raíz cuadrada de 3 (coinciden en los trece primeros decimales)?
¿Cómo se ha obtenido?
¿Cómo se ha obtenido?
lunes, 8 de febrero de 2010
Frobenius y los Mcnuggets
(Con esta entrada participamos en el Primer Carnaval de Matemáticas)
Un número entero positivo “McNugget”, es aquel que es expresable como combinación lineal, con coeficientes enteros no negativos, de los números 6, 9 y 20. Se llama así porque 6, 9 y 20 eran los contenidos de las cajas de McDonald's® Chicken McNuggetsTM.
Hay números que son “McNugget”, como el 30 = 2*9+2*6, que abarcan un número entero de cajas (un pedido normal), y otros que no pueden serlo, como el 11, que no se puede descomponer en sumandos 6, 9 y 20.
Este es un simpático ejemplo de descomposición de un entero N en sumandos extraídos de un conjunto (lista) L. Por ejemplo, el número 10, según la lista (5,3,1) se puede descomponer en 10= 5+5 = 5+3+1+1 = 5+1+1+1+1+1 = 3+3+3+1 = 3+3+1+1+1+1 = 3+1+1+1+1+1+1+1 = 1+1+1…
Las sumas las podemos expresar como combinaciones lineales:
10 = 2*5+0*3+0*1 = 1*5+1*3+2*1 = 1*5+5*1 = …
En el caso de los “McNugget”, los coeficientes serían, evidentemente, el número de cajas que deberíamos pedir.
Generalizando, dado un conjunto de números enteros positivos a1, a2, a3,…an, diremos que otro entero positivo N es representable según ese conjunto si existen coeficientes enteros no negativos x1, x2, x3,…xn tales que N= a1*x1+a2*x2+…an*xn
Según sea el conjunto a1, a2, a3,…an será distinta la discusión de si todos los enteros positivos N son representables en ese conjunto. Nos referiremos a partir de ahora a aquellos en los que que MCD(a1, a2, a3,…an)=1, es decir, que sean coprimos, aunque no necesariamente dos a dos.
Este problema es llamado también de las monedas, porque equivale a discutir si una cantidad de dinero se puede expresar sólo con dos o tres tipos de monedas (o de billetes, o de sellos).
Se puede demostrar que para números N grandes es posible siempre esta expresión de un número como combinación lineal de este tipo (uno de los teoremas de Schur). Existirá, por tanto, un número que sea el mayor para el que no se cumpla, que no sea representable en ese conjunto. Este es el llamado número de Frobenius. Por ejemplo, en los McNugget, el número de Frobenius es 43, porque es el mayor de los números no representables con 6, 9 y 20. Todos los mayores que él lo son.
Encontrar el número de Frobenius para un conjunto de varios números primos entre sí es un problema muy complejo (tipo NP-hard) que sobrepasa los objetivos de este blog, dedicado a las cuestiones de nivel medio.
No obstante, podemos hacer alguna propuesta sobre él.
(a) El que un número N suficientemente grande sea representable siempre lo podemos razonar para el caso de dos coeficientes. Sean A y B enteros positivos primos entre sí. Sabemos que entonces la ecuación Ax+By=N siempre tiene solución: X0=pN-Bt Y0=qN+At, siendo p y q una solución de Ax+By = 1 y t un parámetro. Lo que tienes que investigar es si para N suficientemente grande, X0 e Y0 pueden ser ambos no negativos. Pues a por ello.
Con la ayuda de la hoja de cálculo también se puede investigar algún aspecto de este problema:
(b) Nuestro Buscador de Números Naturales permite encontrar aquellos que sean suma de múltiplos de otros. Así, los números McNugett serán suma de múltiplos de 6, 9 y 20. De esta forma puedes comprobar que el número de Frobenius para ellos es 43.
Sigue estos pasos:
Abre el Buscador de Naturales para Calc en
http://www.hojamat.es/sindecimales/divisibilidad/herramientas/hojas/buscador.ods
o para Excel en
http://www.hojamat.es/sindecimales/divisibilidad/herramientas/hojas/buscador.xls
Borra las condiciones con el botón correspondiente y diseña una búsqueda como suma de múltiplos en “Suma Especial” guiándote por la siguiente imagen (escribe SI, M6, M9…)

Concreta en la parte superior que buscaremos desde 1 hasta 200. Pulsa sobre el botón “Buscar números” y obtendrás una lista en la que a partir del número 44 todos aparecen consecutivos, por lo que se comprueba que 43 es el máximo que no es representable.

Silvester demostró que para dos números a y b coprimos, su número de Frobenius equivale a
g(a,b)=ab-a-b.
Puedes comprobarlo con el Buscador de Naturales. Borra condiciones y diseña una búsqueda sólo con dos múltiplos, y podrás observar que su número de Frobenius cumple la fórmula de Silvester. En la imagen puedes ver el caso de que a=11 y b=8, con lo que g(11,8)=11*8-11-8=69, y a partir del 70 todos son consecutivos.

(c) Hemos preparado un modelo de hoja de cálculo que encuentra todas las posibilidades de representación de un número respecto a otros varios. Por tratarse de un algoritmo voraz, puede tener algún fallo, pero parece funcionar bien.

Puedes descargártelo (dos versiones: Excel y Calc) desde
http://www.hojamat.es/blog/mcnugget.zip
En la segunda hoja dispones de unas breves instrucciones
Un número entero positivo “McNugget”, es aquel que es expresable como combinación lineal, con coeficientes enteros no negativos, de los números 6, 9 y 20. Se llama así porque 6, 9 y 20 eran los contenidos de las cajas de McDonald's® Chicken McNuggetsTM.
Hay números que son “McNugget”, como el 30 = 2*9+2*6, que abarcan un número entero de cajas (un pedido normal), y otros que no pueden serlo, como el 11, que no se puede descomponer en sumandos 6, 9 y 20.
Este es un simpático ejemplo de descomposición de un entero N en sumandos extraídos de un conjunto (lista) L. Por ejemplo, el número 10, según la lista (5,3,1) se puede descomponer en 10= 5+5 = 5+3+1+1 = 5+1+1+1+1+1 = 3+3+3+1 = 3+3+1+1+1+1 = 3+1+1+1+1+1+1+1 = 1+1+1…
Las sumas las podemos expresar como combinaciones lineales:
10 = 2*5+0*3+0*1 = 1*5+1*3+2*1 = 1*5+5*1 = …
En el caso de los “McNugget”, los coeficientes serían, evidentemente, el número de cajas que deberíamos pedir.
Generalizando, dado un conjunto de números enteros positivos a1, a2, a3,…an, diremos que otro entero positivo N es representable según ese conjunto si existen coeficientes enteros no negativos x1, x2, x3,…xn tales que N= a1*x1+a2*x2+…an*xn
Según sea el conjunto a1, a2, a3,…an será distinta la discusión de si todos los enteros positivos N son representables en ese conjunto. Nos referiremos a partir de ahora a aquellos en los que que MCD(a1, a2, a3,…an)=1, es decir, que sean coprimos, aunque no necesariamente dos a dos.
Este problema es llamado también de las monedas, porque equivale a discutir si una cantidad de dinero se puede expresar sólo con dos o tres tipos de monedas (o de billetes, o de sellos).
Se puede demostrar que para números N grandes es posible siempre esta expresión de un número como combinación lineal de este tipo (uno de los teoremas de Schur). Existirá, por tanto, un número que sea el mayor para el que no se cumpla, que no sea representable en ese conjunto. Este es el llamado número de Frobenius. Por ejemplo, en los McNugget, el número de Frobenius es 43, porque es el mayor de los números no representables con 6, 9 y 20. Todos los mayores que él lo son.
Encontrar el número de Frobenius para un conjunto de varios números primos entre sí es un problema muy complejo (tipo NP-hard) que sobrepasa los objetivos de este blog, dedicado a las cuestiones de nivel medio.
No obstante, podemos hacer alguna propuesta sobre él.
(a) El que un número N suficientemente grande sea representable siempre lo podemos razonar para el caso de dos coeficientes. Sean A y B enteros positivos primos entre sí. Sabemos que entonces la ecuación Ax+By=N siempre tiene solución: X0=pN-Bt Y0=qN+At, siendo p y q una solución de Ax+By = 1 y t un parámetro. Lo que tienes que investigar es si para N suficientemente grande, X0 e Y0 pueden ser ambos no negativos. Pues a por ello.
Con la ayuda de la hoja de cálculo también se puede investigar algún aspecto de este problema:
(b) Nuestro Buscador de Números Naturales permite encontrar aquellos que sean suma de múltiplos de otros. Así, los números McNugett serán suma de múltiplos de 6, 9 y 20. De esta forma puedes comprobar que el número de Frobenius para ellos es 43.
Sigue estos pasos:
Abre el Buscador de Naturales para Calc en
http://www.hojamat.es/sindecimales/divisibilidad/herramientas/hojas/buscador.ods
o para Excel en
http://www.hojamat.es/sindecimales/divisibilidad/herramientas/hojas/buscador.xls
Borra las condiciones con el botón correspondiente y diseña una búsqueda como suma de múltiplos en “Suma Especial” guiándote por la siguiente imagen (escribe SI, M6, M9…)

Concreta en la parte superior que buscaremos desde 1 hasta 200. Pulsa sobre el botón “Buscar números” y obtendrás una lista en la que a partir del número 44 todos aparecen consecutivos, por lo que se comprueba que 43 es el máximo que no es representable.

Silvester demostró que para dos números a y b coprimos, su número de Frobenius equivale a
g(a,b)=ab-a-b.
Puedes comprobarlo con el Buscador de Naturales. Borra condiciones y diseña una búsqueda sólo con dos múltiplos, y podrás observar que su número de Frobenius cumple la fórmula de Silvester. En la imagen puedes ver el caso de que a=11 y b=8, con lo que g(11,8)=11*8-11-8=69, y a partir del 70 todos son consecutivos.

(c) Hemos preparado un modelo de hoja de cálculo que encuentra todas las posibilidades de representación de un número respecto a otros varios. Por tratarse de un algoritmo voraz, puede tener algún fallo, pero parece funcionar bien.

Puedes descargártelo (dos versiones: Excel y Calc) desde
http://www.hojamat.es/blog/mcnugget.zip
En la segunda hoja dispones de unas breves instrucciones
viernes, 5 de febrero de 2010
Sumas con simetría
En un libro sobre calculadoras de Elie Vannier se presentaban estas operaciones
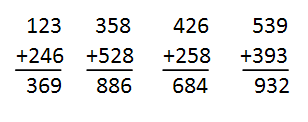 como ejemplo de sumas que forman con su resultado una matriz simétrica
como ejemplo de sumas que forman con su resultado una matriz simétrica
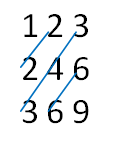 ¿Cuántas de esas sumas de tres cifras existen?
¿Cuántas de esas sumas de tres cifras existen?
Si eliminamos la cifra 0, que produce demasiados casos triviales, resultan 252 sumas, salvo algún error que se haya cometido. La de cifras más pequeñas es 112+112=224 y la última en aparecer 819+179=998
¿Podrías implementar un algoritmo exhaustivo que las hiciera aparecer en una hoja de cálculo?
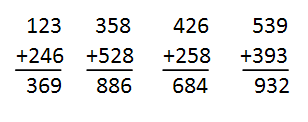 como ejemplo de sumas que forman con su resultado una matriz simétrica
como ejemplo de sumas que forman con su resultado una matriz simétrica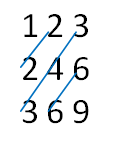 ¿Cuántas de esas sumas de tres cifras existen?
¿Cuántas de esas sumas de tres cifras existen?Si eliminamos la cifra 0, que produce demasiados casos triviales, resultan 252 sumas, salvo algún error que se haya cometido. La de cifras más pequeñas es 112+112=224 y la última en aparecer 819+179=998
¿Podrías implementar un algoritmo exhaustivo que las hiciera aparecer en una hoja de cálculo?
jueves, 21 de enero de 2010
Sumas de los primeros cuadrados o triangulares
Estudiando un tema determinado me he encontrado con esta relación que no conocía:
12+22+32+42+52+…+232+242 = 702
No sé si estará publicada ya en lgún blog, pero la presento aquí por su elegancia y por mi sospecha de que no existen casos similares, salvo el trivial 1. He buscado mediante dos métodos y no he encontrado otro cuadrado que sea suma de los K primeros cuadrados.
Si alguien conoce algo más del tema le rogaría nos lo comunicara.
¿Ocurrirá algo parecido con los números triangulares?:
1+3+6+10+15…+N(N+1)/2 = K(K+1)/2
La respuesta es afirmativa
He descubierto cuatro casos entre 1 y 100000, sin contar el trivial 1=1, en los que la suma de los primeros triangulares produce otro triangular.
El primero es 1+3+6 = 10
¿Cuáles son los otros tres?
Ya puestos a calcular, me he planteado si sumando los primeros números triangulares podremos obtener un cuadrado, o, a la inversa, si sumando los primeros cuadrados la suma será un número triangular. En ambos casos existen soluciones. ¿Sabrías buscarlas?
12+22+32+42+52+…+232+242 = 702
No sé si estará publicada ya en lgún blog, pero la presento aquí por su elegancia y por mi sospecha de que no existen casos similares, salvo el trivial 1. He buscado mediante dos métodos y no he encontrado otro cuadrado que sea suma de los K primeros cuadrados.
Si alguien conoce algo más del tema le rogaría nos lo comunicara.
¿Ocurrirá algo parecido con los números triangulares?:
1+3+6+10+15…+N(N+1)/2 = K(K+1)/2
La respuesta es afirmativa
He descubierto cuatro casos entre 1 y 100000, sin contar el trivial 1=1, en los que la suma de los primeros triangulares produce otro triangular.
El primero es 1+3+6 = 10
¿Cuáles son los otros tres?
Ya puestos a calcular, me he planteado si sumando los primeros números triangulares podremos obtener un cuadrado, o, a la inversa, si sumando los primeros cuadrados la suma será un número triangular. En ambos casos existen soluciones. ¿Sabrías buscarlas?
Suscribirse a:
Comentarios (Atom)