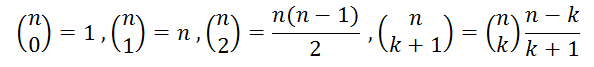Hace un tiempo, publiqué en Twitter (@connumeros) esta identidad:
22622*2*2*6*2*2=2171712
En ella, un número capicúa (o palindrómico), multiplicado
por sus cifras, produce otro capicúa.
Ese mismo día comprobé esta otra igualdad:
22226+2*2*2*2*6=22322.
Por cumplirse la primera igualdad, 22622 pertenece a http://oeis.org/A229550, aunque en la misma no se exige que sea capicúa.
Estas dos propiedades en un mismo número me han animado a
buscar casos parecidos en los que intervengan las cifras y se construya un
número capicúa. Para ello regresaré a una entrada antigua.
Generación con un
producto
En el año 2018 abordé en este blog el caso de números que
permutaban sus cifras si se les sumaba el producto de las mismas. Esto ocurre,
por ejemplo, en 9518=9158+9*1*5*8
(Ver https://hojaynumeros.blogspot.com/2018/09/permutacion-de-cifras-al-sumar-su.html)
En esa entrada informaba de que Derek Orr ya había publicado
casos similares en OEIS en 2014 (Ver http://oeis.org/A247888
y
http://oeis.org/A243102)
En el desarrollo de los cálculos se usaban las funciones
CIFRAS_IDENTICAS y PRODUCIFRAS. Esta última nos será útil en las cuestiones que
abordemos ahora, por lo que se recomienda su repaso en la entrada enlazada.
También usaremos la función ESCAPICUA
(Ver https://hojaynumeros.blogspot.com/2017/10/suma-de-cuadrado-y-capicua.html)
Todos estos antecedentes justifican que el título de
Regresos 11 para esta entrada.
Capicúa igual a otro capicúa
por sus cifras
En el primer ejemplo, un capicúa multiplicado por el
producto de sus cifras produce otro capicúa. No es difícil construir una
búsqueda con esta condición con la función PRODUCIFRAS
Abordamos el primer ejemplo y sus similares: 22622*2*2*6*2*2=2171712
Al tener a nuestra disposición las funciones adecuadas,
bastará buscar aquellos capicúas (con la función ESCAPICUA) que multiplicados
por PRODUCIFRAS produzcan otro capicúa. Exigiremos que el producto de las
cifras sea mayor que uno para evitar trivialidades.
Al realizar la búsqueda se comprueba que existen más casos
de los esperados al principio, y entre ellos, el publicado 22622:
Aunque se programó la búsqueda hasta 100000, los resultados se detienen en el ejemplo ya conocido. Al proseguir más adelante aparecieron los casos 112211, 121121, 211112, lo que hace sospechar que casi todos los que aparezcan tendrán un producto igual a 2 o 3. Para profundizar, tradujimos la búsqueda al lenguaje PARI:
2, 3, 22, 77, 121, 131, 212, 464, 1221, 2112, 11211, 11311,
12121, 21112, 22622, 112211, 121121, 211112, 1112111, 1113111, 1121211,
1211121, 2111112, 2223222, 4213124,…
Se puede afirmar que esta sucesión es infinita, pues
pertenecerán a ella todos los números capicúas del tipo 111…11211…111,
111…11311…111, 111…212…111 y otros similares. Entre ellos aparecerán otros como
4213124, de desarrollo más inesperado.
Capicúa más suma de
sus cifras
Otros ejemplos se pueden construir sumando las cifras en
lugar de usar su producto. También contamos con la función SUMACIFRAS, que se
puede estudiar, por ejemplo, en la entrada https://hojaynumeros.blogspot.com/2015/03/autonumeros-1.html
Bastará exigir que N (capicúa) más SUMACIFRAS(N) sea también
capicúa. Los primeros ejemplos son:
Estos son los únicos números con esta propiedad entre los menores de 10^7, según se comprueba con PARI. Sin embargo, si se amplía el rango de búsqueda aparecen otros, como el 73999999999937, según se ve en https://oeis.org/A229622.
En esa página se afirma que la sucesión es infinita, porque
se pueden añadir, con más cifras, números similares a 1099999999999901. No es
difícil razonarlo.
Número no capicúa
genera un capicúa al multiplicar por sus cifras
Podemos eliminar la condición de que el número que engendra
un capicúa no sea él mismo de ese tipo al multiplicar por sus cifras. En este caso, además de soluciones predecibles,
aparecen otras que parecen ser debidas a casualidades:
Es predecible que 35*3*5=525, pero los dos últimos de la tabla sorprenden por su similitud.
Número no capicúa
genera un capicúa al sumar sus cifras
Si en lugar de multiplicar por sus cifras, las sumamos, se
amplían los ejemplos:
Los números de la primera columna están publicados en https://oeis.org/A229545, y allí se explica algunos ciclos de las últimas cifras de sus elementos.
La última columna parece contener todos los capicúas a
partir del 11, pero no es así, porque, por ejemplo, falta el 121. En efecto, es
imposible que cumpla la condición:
Si partimos de un número de dos cifras 10a+b tendríamos
10a+b+a+b=11a+2b=121
Como 2b<20, ningún múltiplo de 11 inferior a 121 y con a<10
presenta una diferencia menor de 20 con él. No nos valdría 99 ni 110.
Si el número tuviera tres cifras tampoco sería posible
100+10a+b+1+a+b=101+11a+2b, y tendríamos la misma situación.
El número 121 es colombiano o autonúmero
(Ver nuestra explicación en https://hojaynumeros.blogspot.com/2015/03/autonumeros-1.html)
Según esto, si disponemos, como es en este caso, de las
funciones ESCAPICUA y ESAUTO (ver entrada enlazada), bastará exigir las dos
condiciones para obtener la lista de capicúas que no admiten la propiedad que
estamos estudiando:
Están publicados en https://oeis.org/A332970
Números
con cifras crecientes
Nos queda comprobar casos similares
al recordado al principio de este estudio:
22226+2*2*2*2*6=22322
Con multiplicación
Ya hemos usado en otra ocasión la función CIFRAS_CRECIENTES,
que determina si un número posee sus cifras crecientes en sentido amplio.
Puedes consultar la siguiente entrada:
https://hojaynumeros.blogspot.com/2022/06/numeros-con-cifras-crecientes-o.html
Con esta función es fácil encontrar números con cifras
crecientes tales que, al multiplicar por todas sus cifras, resulte un capicúa.
Esos son los primeros resultados:
Con la suma
Volvemos a intentarlo, pero sumando el producto de las
cifras, e ignorando los productos nulos:
Entre otros muchos resultados menores, aparece el que encabezaba este texto: 22226+2*2*2*2*6=22322.
Con esto finalizamos la exploración de estas curiosidades
similares entre sí. Se han dejado algunas sin estudiar, como es nuestra costumbre,
para dejar otras posibilidades de exploración y no extender demasiado este
texto.
Algunos resultados están inéditos, pero el autor no los va a
publicar en OEIS.
Al igual que en temporadas anteriores, con esta entrada de junio
termina la 2023-24. En verano esperan otras actividades, y ya volverán más
curiosidades en septiembre. Gracias por leerme.