Al igual que con los divisores habituales y los unitarios, los divisores semiprimos pueden dar lugar a funciones SIGMA y TAU.
En la entrada anterior
usamos la función div_semi para
encontrar y contar los divisores semiprimos de un número. Esta sería la función
TAU en este caso. Bastará cambiar ligeramente estas líneas de su código para
sumar en lugar de contar o usar potencias:
If essemiprimo(k) And n / k = n \ k Then ‘Es
divisor semiprimo
nn = n: e = 0 ‘Posibles exponentes
If repe Then ‘Caso de repetición
While nn / k = nn \ k: e = e + 1: nn = nn / k:
Wend
End If
If repe Then m = m + e Else m = m + 1
La última línea cuenta
divisores, pero si la sustituyéramos por m=m+e*k^t o m=m+k^t nos serviría para
el cálculo de la familia de las SIGMAS, que suman divisores, o sus cuadrados, o
también cualquier potencia. Incluso si el exponente es 0, la función seguiría
contando en lugar de sumar, es decir, que sería TAU. Estos pequeños cambios en
la función div_semi los daremos por
supuestos en cada caso.
Funciones SIGMA
Tradicionalmente, estas
funciones han sumado los divisores de un número o bien alguna potencia de
ellos. En el caso de los semiprimos les añadiremos _S para distinguirlas. Así
SIGMA3_S sumará los cubos de los divisores semiprimos. Por ahora no
consideraremos las repeticiones.
La más sencilla será
SIGMA_S, que sumará los divisores semiprimos sin contar repeticiones. En la
función div_semi sustituiremos m=m+1
por m=m+k. De esta forma podemos calcular la suma sin repetición si usamos el
parámetro repe=0. Por ejemplo, para
330 pediríamos DIV-SEMI(330;0). En la imagen podemos comparar la lista de divisores
semiprimos con su suma:
Así que, en este caso, SIGMA_S(330)=141
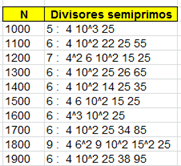
El resultado, para los
primeros números es:
Podemos comparar las dos últimas columnas para verificar las sumas.
Las sumas de la segunda
columna están publicadas en https://oeis.org/A076290
Tambien, si cambiamos ligeramente la versión en PARI,
obtendremos los mismos resultados. Esta sería la nueva versión:
sigma_s(n)= sumdiv(n, d, (bigomega(d)==2)*d)
print(sigma_s(330))
Su resultado:
Hemos intentado buscar números s_perfectos, que coincidan con la suma de sus divisores semiprimos, pero no hemos encontrado ninguno para números inferiores a 2*10^6. Entre los 20 primeros son todos s_deficientes, y, según nuestras búsquedas, 30 es el único s_abundante, pues sus divisores primos suman 31: 6+10+15=31
Algunos tipos de
sigma_s
Los resultados de la suma de divisores pueden presentar
alguna curiosidad. Recorremos posibilidades:
Sigma_s semiprima
Si un número N es semiprimo, el valor de SIGMA_S(N) coincide
con N, luego será otro semiprimo. Si no lo es, sí puede serlo SIGMA_S. Estos
son los primeros ejemplos:
Sigma_s cuadrada
Dejamos aparte las sigmas de las potencias de primos, que
son todas cuadradas, e investigamos si existen en otros casos. El resultado es
Sigma_s prima
Por
último, destacamos que aparecen bastantes sigmas primas en los primeros
números, y que vuelven a aparecer números poderosos.
Las otras sigmas
Sumas de cuadrados
Podemos
sumar los divisores semiprimos previamente elevados al cuadrado, con lo que
lograríamos SIGMA2_S. Basta un pequeño ajuste en nuestras funciones, usando la
operación m=m+k^2
Los
primeros resultados serían
Por
ejemplo, SIGMA2_S(2160)=458, porque esa es la suma de los cuadrados de sus
divisores semiprimos:
4^2+6^2+9^2+10^2+15^2=458
El valor de SIGMA2_S(N) es mayor o igual al de SIGMA_S(N), lo que nos abre la posibilidad de que aquí sí existan números s2_perfectos. Y es así, porque en la tabla vemos que SIGMA2_S(16)=16. ¿Existirán más? Los buscamos, y los primeros son: 16, 81, 625 y 2401, es decir, potencias cuartas de primos, en los que su divisor semiprimo es un cuadrado de primo, y al elevarlo al cuadrado, resulta N, que así se convierte en un s2_perfecto.
Hemos acudido a la velocidad de PARI, y al menos, para números inferiores a 10^6, todos los s2_perfectos son potencias cuartas de primos:
Otras sigmas de potencias
Las sumas con cubos son: