Este blog es un complemento natural de mi página http://www.hojamat.es. Por ello, se dedicará a los temas numéricos tratados con Hoja de Cálculo y a la estructura y prestaciones de esta. Su nivel será elemental o medio, y su orientación lúdica e investigadora.
miércoles, 28 de octubre de 2015
Damos vueltas a los triangulares cuadrados (1) Generación.
Generación de la sucesión
Dos entradas del blog de John D. Cook (http://www.johndcook.com/blog/2015/08/20/when-is-a-triangle-a-square/ y siguiente) me han animado a volver a tomar el tipo de entrada al que llamé “dar vueltas” a un tema o concepto. Lo haré sobre estos números:
0, 1, 36, 1225, 41616, 1413721, 48024900, 1631432881,… (http://oeis.org/A001110)
Evidentemente, tienen en común el ser triangulares y cuadrados a la vez. Puedes leer un desarrollo sencillo y claro en este documento:
http://www2.caminos.upm.es/Departamentos/matematicas/revistapm/revista_impresa/vol_IV_num_1/jue_mat_num_triang.pdf
Me he dado cuenta de que es un concepto sencillo pero que da lugar a bastantes reflexiones, algoritmos y repasos de teoría.
Nosotros seguiremos en parte este documento para iniciar el tema.
Búsqueda de números triangulares cuadrados
Un número triangular tiene por fórmula n(n+1)/2 y un cuadrado m2. Aquellos números que participen de las dos características tendrán que cumplir la igualdad
De esta igualdad deducimos esta otra mucho más práctica:
O bien
Con cambio de variable se convierte en una ecuación de Pell:
Esta ecuación la tenemos muy estudiada
http://hojamat.es/parra/pell.pdf (documento de Rafael Parra)
http://hojaynumeros.blogspot.com.es/2010/02/ecuacion-de-pell.html
Disponemos además de una hoja de cálculo para ayudar a resolverla:
http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#pell
Usamos esta herramienta para el coeficiente 8 y el segundo miembro 1 y nos dan las primeras soluciones:
(1,0) (3,1) (17,6) (99,35) (577,204) (3363,1189) (19601,6930) (114243, 40391),…
Por recurrencia:
Según la teoría de la ecuación de Pell, las soluciones aparecen con las recurrencias (en este caso) xn=3*xn-1+8*yn-1 yn=3*yn-1+1*xn-1. Por ejemplo, 99=3*17+8*6, 35=3*6+1*17.
Ahora sólo nos queda elevar al cuadrado las soluciones de y (que equivalen a la variable m de la primera igualdad que planteamos) y nos resultarán los triangulares cuadrados:
020, 12=1, 62=36, 352=1225, 2042=41616, 11892=1413721,…
Primer algoritmo
El estudio que acabamos de desarrollar nos da una pista para la generación de términos triangulares cuadrados: Iniciamos dos variables X=1, Y=0, y en cada paso del algoritmo convertimos X en 3X+8Y y la Y en 3Y+X. Terminado el cálculo presentamos el valor de Y2 como siguiente triangular cuadrado. En el Basic de las hojas de cálculo quedaría así:
Sub triangcuad()
Dim x, y, x1, y1, i, t, fila
x = 1: y = 0 ‘Valores de inicio
fila = 3 ‘Fila inicial
Cells(fila, 4).Value = 0 ‘El primer valor es un cero
For i = 1 To 8 ‘Calculamos sólo ocho
x1 = 3 * x + 8 * y ‘Iteración para x
y1 = 3 * y + x ‘Iteración para y
x = x1
y = y1
t = y * y ‘Número triangular cuadrado
fila = fila + 1
Cells(fila, 4).Value = t ‘Se presenta el resultado
Next i
End Sub
Obtendríamos:
El que el último se nos ofrezca en coma flotante nos da idea de las limitaciones de la hoja para cálculos con enteros de muchas cifras. Si acudimos a PARI no nos encontraremos con esas limitaciones. Prueba este código:
{x=1;y=0;print(0);while(x<10^10,x1=3*x+8*y;y1=3*y+x;x=x1;y=y1;t=y^2;print(t))}
En pocos segundos te presenta los triangulares cuadrados menores que 10^10.
Relación de recurrencia con una sola variable
Por la naturaleza de su definición podemos esperar que estos números sigan una relación de recurrencia de segundo orden. Para encontrar su expresión, que será del tipo
An=aAn-1+bAn-2+c usaremos los valores iniciales 0, 1, 36, 1225, 41616 para plantear:
36=a*1+b*0+c
1225=a*36+b*1+c
41616=a*1225+b*36+c
Resolvemos
1189=35a+b
40391=1189a+35b
1224=36a y a=34, b=-1 y c=2
Según los cálculos anteriores, la relación de recurrencia será
An=34An-1-An-2+2
Es la misma que propone John D. Cook en su blog.
En este blog no olvidamos la hoja de cálculo. Intenta una resolución como la de la imagen usando cálculo matricial:
A partir de esta escritura matricial del sistema de ecuaciones, creamos debajo la matriz inversa de los coeficientes con MINVERSA, y a su derecha su producto por los términos independientes con MMULT:
Conseguimos así la misma solución 34, -1, 2
Segundo algoritmo
La relación de recurrencia nos permite un segundo algoritmo para encontrar los triangulares cuadrados. El que describimos a continuación presenta los nueve primeros (después existen problemas de coma flotante)
Sub triancuad1()
Dim m, n, p, k, fila
m = 0: n = 1 ‘Valores iniciales
fila = 3
Cells(1, 3).Value = m ‘presenta los dos primeros términos
Cells(2, 3).Value = n
For k = 1 To 7
p = 34 * n - m + 2 ‘relación de recurrencia
Cells(fila, 3).Value = p: fila = fila + 1 ‘presenta los siguientes términos
m = n: n = p ‘cada término se convierte en el anterior
Next k
End Sub
Los términos rellenarán una columna de hoja de cálculo:
Siguiendo nuestra costumbre, lo traducimos a PARI para conseguir más términos:
{x=0;y=1;print(0);print(1);for (k=1, 20, z=34*y-x+2;print(z);x=y;y=z)}
No resistimos la tentación, al igual que propone J.C. Cook, de intentar una versión recursiva en forma de función. Funciona muy bien en hoja de cálculo:
Public Function ftriangcuad(n)
If n < 2 Then
ftriangcuad = n
Else
ftriangcuad = 34 * ftriangcuad(n - 1) - ftriangcuad(n - 2) + 2
End If
End Function
No necesita explicación. La tabla siguiente se forma con gran rapidez de cálculo:
Fórmula directa
Si lees el capítulo sobre sucesiones recurrentes en nuestra publicación Sucesiones (http://www.hojamat.es/publicaciones/sucesiones.pdf) entenderás que a partir de la fórmula de recurrencia es posible encontrar la expresión directa de cada término (fórmula del término general). Sólo insertamos la captura de pantalla de nuestra hoja de cálculo Recurrencias
(http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#recurre2) en la parte homogénea de la recurrencia:
Con un ligero retoque y la interpretación de los decimales llegamos a la propuesta por John D. Cook:
El uso de la raíz cuadrada de 2 le quita utilidad en nuestro trabajo, por lo que intentaremos prescindir de ella. Para ver la influencia del formato de coma flotante, la implementamos en hoja de cálculo, y el resultado es similar al de los algoritmos anteriores:
Función generatriz
Para quien no lo sepa, diremos que la función generatriz de una sucesión, si se desarrolla como una serie de potencias, poseerá como coeficientes de esas potencias de x los términos de la sucesión.
En el caso de los números triangulares cuadrados la función generatriz es
(ver http://oeis.org/A001110)
Con esta sencilla orden de PARI podemos comprobar su desarrollo.
print(taylor(x*(1+x)/((1-x)*(1-34*x+x^2)),x,20))
Tercer algoritmo
Finalizamos la entrada con la presentación de un algoritmo de los que llamamos “ingenuos”, que no usan la teoría para simplificar los cálculos, pero sí la fuerza bruta de la velocidad de proceso. En este caso obligaremos a los números naturales a ir creciendo hasta alcanzar un cuadrado, y después a la inversa, que los cuadrados avancen hasta alcanzar un triangular. Cuando se llegue a una igualdad se imprime el resultado. A pesar de su simplicidad, no resulta lento. Es éste:
Sub triancuad2()
Dim i, j, m, n, k, fila
m = 3: n = 4: i = 2: j = 3 ‘Se inician las variables
k = 10 ^ 7
fila = 3
Cells(fila, 3).Value = 1: fila = fila + 1
While m < k ‘Busca soluciones menores que k
While m <= n ‘Los triangulares crecen
If m = n Then Cells(fila, 3).Value = m: fila = fila + 1 ‘Hay igualdad
i = i + 1: m = m + i
Wend
While n <= m ‘Los cuadrados crecen
If m = n Then Cells(fila, 3).Value = m: fila = fila + 1 ‘Hay igualdad
j = j + 2: n = n + j
Wend
Wend
End Sub
Dejamos a los lectores el estudio de por qué funciona este algoritmo para descubrir los triangulares cuadrados. Como los anteriores, llega a los mismos resultados, en este caso hasta 10^7.
domingo, 18 de octubre de 2015
Sucesión de Recamán
Estudiamos hoy una original sucesión que Bernardo Recamán Santos envió a N. J. A. Sloane en 1991 para su colección, y que desde entonces ha originado múltiples desarrollos, incluso musicales (ver https://www.youtube.com/watch?v=h3qEigSSuF0).
Su definición es la siguiente (versión con a1=1):
a1=1
an = an-1 – n, si este valor es positivo y no figura ya en la sucesión
an = an-1 + n, en caso contrario.
Sus primeros términos son: 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8, 25, 43, 62, 42, 63, 41, 18, 42, 17, 43, 16, 44, 15, 45, 14, 46, 79, 113, 78, 114, 77, 39, 78, 38, 79, 37, 80, 36, 81, 35, 82, 34, 83, 33, 84, 32, 85, 31, 86, 30, 87, 29, 88, 28, 89, 27, 90, 26, 91, 157,… (existe otra versión que comienza en 0, idéntica a esta en todo lo demás http://oeis.org/A005132)
El punto clave, y que nos permitirá estudiar su programación con hoja de cálculo es el de no figura ya en la sucesión, pues esto obliga a mantener en memoria un registro de los valores anteriores ¿Cómo solucionarlo en una hoja de cálculo? Intentaremos varias posibilidades.
Desarrollo de la sucesión mediante celdas
Las celdas de una hoja sirven de memoria en cualquier proceso, por lo que comenzaremos el estudio por ahí. En la imagen verás la formación de la sucesión de Recaman en la columna E, junto a otra auxiliar D que hemos añadido por simple comodidad:
La columna D contiene, simplemente, la diferencia an-1 – n, que se obtiene con las expresiones =E2-FILA(),=E3-FILA(),=E4-FILA(),…aprovechando la función FILA, que aquí representará el valor de n en la definición. Por eso hemos creado la sucesión a partir de la primera fila. Si ese valor en la columna D es positivo y no ha salido ya, será el valor del siguiente término de la sucesión. Por eso no extrañará que algunos de estos valores figuren en la columna E que estudiaremos a continuación.
En dicha columna E hemos construido una fórmula un poco compleja. Esta es la correspondiente a la celda E3:
=SI(Y(D3>0;CONTAR.SI(E$1:E2;D3)=0);D3;FILA()+E2)
Recuerda que D3 contiene an-1 – n, que en este caso sería a2 – 2.
La fórmula comienza con un SI, puesto que la definición se basa en una alternativa. Después una Y, ya que existen dos condiciones: una que D3 sea positiva, y otra que no figure ya en la columna E. La primera se resuelve con D3>0 y la segunda con CONTAR.SI(E$1:E2;D3)=0. Usamos CONTAR.SI para ver si D3 ha salido ya. Si el CONTAR da cero, es que no ha salido, y se admite. Observa que se busca desde la primera celda E$1 (referencia absoluta) hasta la anterior E2.
Si ambas condiciones se cumplen, la función SI devuelve D3, como era de esperar, y, en caso contrario, FILA()+E2, es decir, an-1 + n.
Rellenando esta fórmula hacia abajo obtendremos la sucesión hasta el término que deseemos. Lo hemos efectuado hasta 2000 términos, para crear un gráfico similar al que figura en las publicaciones que tratan esta sucesión, en este caso de tipo lineal:
Llaman la atención en el mismo las fuertes oscilaciones que se producen en algunos intervalos, en los que los términos sufren incrementos alternativamente positivos y negativos, como en este:
En este tramo, las diferencias positivas decrecen de uno en uno y las negativas de tres en tres.
Si hubiésemos usado un gráfico de dispersión entre n y an obtendríamos
Pertenencia de todos los enteros positivos
N. J. A. Sloane conjeturó que cualquier entero positivo terminará apareciendo en la sucesión, y de hecho, estas son las posiciones en las que figuran los primeros términos: 1, 4, 2, 131, 129, 3, 5, 16, 14, 12, 10, 8, 6, 31, 29, 27, 25, 23, 99734, 7, 9, 11, 13, 15, 17, 64, 62, 60, 58, 56,… https://oeis.org/A057167
Nosotros podemos construir esta sucesión con la función COINCIDIR. Observa la imagen:
Se han reproducido los valores de las posiciones de 1, 2, 3,… salvo la del 19, que al ser 99734 excedía nuestro ámbito de estudio. Como uno de los objetivos de este documento es el aprendizaje de las técnicas de la hoja de cálculo, reproducimos la fórmula usada. La columna F contiene los primeros números naturales, y recuerda que E contiene la sucesión. Bastará, pues, usar la función COINCIDIR, para ver si el número dado figura o no en la sucesión, y en qué posición, que es lo que nos devuelve esa función COINCIDIR. Por ejemplo, para el 5 usamos esta fórmula: =COINCIDIR(F5;E$1:E$2000;0). En ella F5 es el valor 5 y E$1:E$2000 el rango de búsqueda (hemos llegado a 2000 elementos). El 0 final indica que buscamos valores exactos, y la función nos devuelve 129, que es la posición en la que aparece el 5, como puedes ver en este recorte de la tabla:
En ella también aparece el 131, número de orden del 4.
Si hubiéramos creado una tabla de muchos más términos terminaríamos por encontrar en ella todos los números naturales. Eso es lo que conjetura Sloane.
Función RECAMAN(n)
El desarrollo anterior puede ser más o menos interesante, pero, como hemos procedido en casos parecidos, sería muy útil obtener un valor de la sucesión por cálculo directo (en realidad, en su interior sería recursivo), de forma que dado un número de orden, existiera una función que nos devolviera el término correspondiente de la sucesión de Recaman. Esto choca con el mismo inconveniente que en el caso del cálculo progresivo, y es el almacenamiento de los valores anteriores. Esa función debería contener un vector o tabla que memorizara dichos valores. En el Basic de las hojas de cálculo no existe un dimensionamiento dinámico de un vector en función de n, por lo que no sería práctico. Por ello hemos pensado almacenar los valores previos en un string o cadena de caracteres, que crece dinámicamente sin problemas.
La función cuya codificación presentamos ahora almacena los valores previos de la sucesión en el string prev$, pero para que no se den ambigüedades, rodea cada número de dos almohadillas #, es decir, almacenamos un 12 como #12#, para evitar que se confunda con 112, que sería #112# en nuestro sistema. Es un truco que nos evitará muchos problemas. También deberemos suprimir el espacio en blanco que las hojas añaden a los números, pues, si no, el 12 se podría codificar como # 12# y no ser detectado. Este cambio lo efectuará la función AJUSTA, que es la siguiente (quien no tenga interés en esto puede pasar a la función principal):
Public Function ajusta(a$) As String
If Mid(a$, 1, 1) = " " Then a$ = Right$(a$, Len(a$) - 1)
ajusta = "#" + a$ + "#"
End Function
Disponiendo de esta función auxiliar ya podemos describir la función RECAMAN(n). Es esta:
Public Function recaman(n)
Dim prev$, sd$
Dim d, ant, reca, i
prev$ = " #1# "
ant = 1 ‘Inicia los valores de la sucesión de Recaman
If n = 1 Then
reca = 1 ‘Caso en el que n=1
Else
For i = 2 To n
d = ant – i ‘Calculamos la diferencia an-1 – n
If d > 0 Then
sd$ = ajusta(Str$(d)) ‘Si la diferencia es positiva, vemos si ya figura en la sucesión
If InStr(prev$, sd$) = 0 Then ‘Usamos InStr para ver si la diferencia figura en el string
reca = d ‘Si no está, la admitimos como nuevo valor
Else
reca = ant + i ‘Si ya figura en la sucesión, usamos la definición alternativa
End If
Else
reca = ant + i ‘Si es negativa, también usamos la definición alternativa
End If
sd$ = Str$(reca) ‘Incorporamos el nuevo término al string que los recuerda
prev = prev + ajusta(sd$)
ant = reca
Next i
End If
recaman = reca
End Function
Copia, si así lo deseas, estas dos funciones en tu hoja de cálculo, y así podrás jugar un poco con esta sucesión. Por ejemplo, puedes descubrir estas curiosidades o ampliarlas:
Elementos repetidos
El primer caso de términos repetidos en la sucesión de Recaman es el 42, que aparece en el índice 20 y en el 24: recaman(20)=recaman(24)=42. Dado un término, no es difícil encontrar el siguiente con el mismo valor. Hemos señalado que el primer repetido es el 42, en los lugares 20 y 24 Dado otro valor, ¿existirá otro con el mismo valor?¿cuál será la siguiente aparición?
Esta cuestión y otras parecidas podemos resolverla con esta función:
Public Function sig_recaman(indi)
Dim v, j, v1
v = recaman(indi)
j = indi
v1 = 0
While v <> v1
j = j + 1
v1 = recaman(j)
Wend
sig_recaman = j
End Function
En ella, dado un número de orden, se busca la siguiente aparición del término correspondiente a ese número de orden. Se le incluye un tope de 10^4 para evitar el bloqueo de la función. Como esta última situación es la más frecuente, sólo destacaremos los casos contenidos en http://oeis.org/A064284
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1,…
En ellos se descubre que repeticiones hay pocas, y casi siempre de sólo dos elementos. Con nuestra función sig_recaman se pueden comprobar algunas:
Recaman(20)=recaman(24)=42
Otros casos tardan mucho en aparecer y no merece la pena seguir por este camino.
Términos iguales a su número de orden
También existen muy pocos. Se puede plantear que recaman(n)=n y ver qué pasa. Sólo encontraremos recaman(1)=1, recaman(1520)=1520, recaman(9317)=9317 y alguno más. Los demás, si existen, sobrepasan nuestra capacidad de cálculo, ya que pertenecerían a esta sucesión
http://oeis.org/A064568
3, 11, 21, 39, 76, 248, 844, 1520, 2752, 9317, 17223, 31221, 57071, 99741, 589932, 58056875, en los que el término es múltiplo del número de orden.
El mismo caso, pero con una unidad de diferencia
¿Pueden ser n y recaman(n) número consecutivos en cualquiera de los dos sentidos?
Podemos plantear la condición ABS(RECAMAN(N)-N)=1 y hemos encontrado recaman(2)=3 y recaman(10)=11. Entre los números menores que 3000 no hay más.
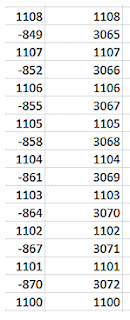
A continuación incluimos la tabla de los números N menores que 1000 cuya diferencia con RECAMAN(N) es menor que 10
Una vez que tienes a tu disposición la función RECAMAN puedes emprender tus propias búsquedas.
jueves, 8 de octubre de 2015
Grupos de potencias en Zn (4) - Índices modulares
Índices modulares
En la entrada anterior estudiamos las raíces primitivas, elementos del grupo multiplicativo Z*n de las unidades en Zn (números coprimos con n), tales que su gaussiano es máximo y coincidente con j(n). Estas raíces, mediante sus potencias, engendran todo Z*n, luego un elemento inversible cualquiera coincidirá con una potencia de la raíz primitiva. El exponente comprendido entre 0 y j(n)-1 que logra esta coincidencia recibe el nombre de índice del elemento respecto a la raíz primitiva. También es llamado logaritmo discreto.
Es decir; si a es una raíz primitiva y b un elemento inversible, existe un exponente k en el intervalo (0, j(n)-1) tal que akºb, y a ese exponente le llamaremos índice de b respecto a la raiz a.
Por ejemplo, el módulo 7 posee dos raíces primitivas. La raíz 3 engendra mediante potencias todos los elementos desde 1 a 6 (por ser 7 primo son todos inversibles), 30º1, 31º3, 32º2, 33º6, 34º4 y 35º5. Cada uno de los exponentes es el índice de ese elemento.
La función índice que asigna a cada elemento inversible el exponente de la menor potencia de la raíz primitiva que lo engendra la podemos representar por inda(b) o simplemente ind(b) si se conoce la raíz. También podemos representarlo como un logaritmo, que en este caso recibe el nombre de logaritmo discreto. En el ejemplo anterior ind3(6)=3, ind3(4), ind3(4)=4,…Si existe una raíz primitiva, todos los elementos inversibles de Zm tendrán definido el índice.
Al ser un exponente, las propiedades del índice o logaritmo discreto son previsibles (supongamos módulo m):
El cálculo de los índices en grupos complejos no es fácil, aunque se han creado muchos algoritmos eficientes, y por eso los índices son usados en algunos sistemas criptográficos.
Aquí nos limitaremos, como siempre, a casos sencillos con los que aprender los conceptos. Hemos creado en nuestra hoja GAUSSIANO
http://www.hojamat.es/sindecimales/congruencias/herramientas/herrcong.htm#gaussiano
un confeccionador automático de tablas de índices para un módulo dado. Sólo tienes que escribir dicho módulo, y pulsar un botón para que aparezca la tabla, si es que existen raíces primitivas. Aquí tienes la del módulo 54:
En columna aparecen los elementos inversibles de Z54, que hay 18, porque j(54)=18. En la fila superior tenemos las raíces primitivas, que por ser 54 de la forma 2pk (2*33), existen con seguridad, y son 6, ya que j(j(54))=6. Con ella podemos encontrar el índice de cualquier inversible. Por ejemplo, el índice de 37 respecto a 23 es 12, lo que indica que 2312=37.
Ecuaciones potenciales
Las tablas de índices nos pueden servir para resolver la ecuación
El comportamiento de los índices como logaritmos nos permite transformar esta ecuación en otra lineal, eligiendo cualquier raíz primitiva b y aplicando índices en ambos miembros respecto a ella.
Según la teoría de las ecuaciones lineales en Zm, si llamamos d al MCD(n, j(m)), el índice de a ha de ser múltiplo de d para que exista solución. En ese caso basta despejar el índice de x y buscar después el valor de x en las tablas. Podíamos haber automatizado todo el proceso, pero parece que se aprende más de esta forma.
Ejemplo: Resolver x6º37 (mod 54
En primer lugar encontramos que j(54)=18 (ver tabla y párrafos anteriores), luego d=MCD(6,18)=6. En la tabla citada buscamos el índice de 37 respecto a la raíz primitiva 5 y encontramos que es 12. Por tanto, como 12 es múltiplo de 6, deberá existir una solución (en realidad, según las propiedades de las ecuaciones lineales, deberían aparecer 6). Tomamos índices respecto al 5:
6*ind5(x)ºind5(37) (mod 54 º12
ind5(x)º12/6=2.
Buscamos en la tabla qué inversible tiene índice 2 respecto a la raíz primitiva 5, y nos resulta 25. Comprobamos:
251º25; 252º25*25º31; 253º25*31º19; 254º25*19º43; 255º25*43º49; 256º25*49º37
Así comprobamos que 25 es una solución de la ecuación propuesta. Pero hemos asegurado que existen otras cinco soluciones, que se pueden leer en la tabla si hubiéramos usado otra raíz primitiva. Son estas: 13, 43, 31, 7 y 49. Esto completa el conjunto de seis soluciones de la ecuación propuesta.
Otras ecuaciones de ese tipo no tienen solución. Por ejemplo:
x7º12 (mod 49
Formamos la tabla de índices módulo 49 y vemos que ind3(12)=11, que j(49)=42 y MCD(7,42)=7, pero 11 no es múltiplo de 7, luego no existe solución. Hemos creado una tabla con las séptimas potencias de los inversibles de Z*49 y sólo nos resultan seis resultados posibles: {1, 30, 31, 18, 19, 48}, y el 12 no está entre ellos.
El ejemplo anterior nos da una pista para descubrir si un resto dado es cúbico, bicuadrado o de otro orden en un módulo dado. Por ejemplo, ¿es resto bicuadrado 15 en módulo 22? Planteamos a4º15 (mod 22 y analizamos:
Formamos la tabla de índices módulo 22
j(22)=10 y MCD(4,10)=2, luego ind(15) ha de ser múltiplo de 2. Según la tabla, se cumple para cualquier raíz primitiva, luego sí es un resto bicuadrado. Podemos encontrar su raíz cuarta:
4ind(a)=2, luego ind(a)=2/4 (mod 22 = 6
El 3 posee índice 6, y cumple 34º15 (mod 22, luego existe la raíz bicuadrada de 15, y este valor 15 es resto bicuadrado (sólo hemos investigado una posibilidad, pero con una basta).
Suscribirse a:
Entradas (Atom)