Números aritméticos (1) - Concepto y ejemplos

Concepto y ejemplos

Con esta entrada comenzamos una serie dedicada a los números aritméticos.  Su publicación podrá organizarse de forma consecutiva, o bien, por necesidades de actualidad, ser intercalada con entradas dedicadas a otros temas.

Los números aritméticos son aquellos en los que el promedio de sus divisores positivos es un número entero. Expresado de otra forma, aquellos en los que su función TAU (número de divisores) divide a su función SIGMA (suma de divisores). Su similitud con nuestros números AROLMAR nos ha motivado a estudiarlos.

(ver http://www.hojamat.es/publicaciones/arolmar.pdf)

El interés de estos números no está en descubrirlos, ya que son abundantes, están publicados (https://oeis.org/A003601) y son fáciles de encontrar. Basta exigir que TAU(N) divida a SIGMA(N). Ambas funciones las puedes encontrar implementadas para hoja de cálculo en este blog y en nuestras publicaciones. Aquí nos interesaran más sus distintos tipos y propiedades.

En la siguiente tabla hemos organizado una búsqueda:

 

Observamos que son aritméticos 1, 3, 5, 6, 7, 11, 13, 14 y 15.

Los primeros, ya publicados, son:

1, 3, 5, 6, 7, 11, 13, 14, 15, 17, 19, 20, 21, 22, 23, 27, 29, 30, 31, 33, 35, 37, 38, 39, 41, 42, 43, 44, 45, 46, 47, 49, 51, 53, 54, 55, 56, 57, 59, 60, 61, 62, 65, 66, 67, 68, 69, 70, 71, 73, 77, 78, 79, 83, 85, 86, 87, 89, 91, 92, 93, 94, 95, 96, 97, 99, 101, 102, 103, 105,...

Para quienes no tengan interés en las dos funciones SIGMA y TAU, adjuntamos una sencilla función en Vbasic para Excel y Calc:

function esaritmetico(n) as boolean

dim t,s,i,c

t=0 'variable para TAU
s=0 'variable para SIGMA
for i=1 to n
if n/i=n\i then 'se trata de un divisor
t=t+1 'incrementa TAU
s=s+i 'incrementa SIGMA
end if
next i
c=s/t' cociente entre SIGMA y TAU
if c=int(c) then esaritmetico=true else
esaritmetico=false
End function

Aplicando esta función a cualquier buscador obtenemos la lista de números aritméticos.

Por ejemplo, esta es la lista de ellos entre 1000 y 1020:

 

Observamos que casi todos los números de ese rango son aritméticos. Más adelante combinaremos esta función esaritmetico con otras, para buscar propiedades interesantes.

Para búsquedas con PARI, la mejor función es la publicada en OEIS:

is(n)=sigma(n)%numdiv(n)==0 \\ Charles R Greathouse IV, Jul 10 2012

En la siguiente imagen se ha usado esta función en la página oficial de PARI, para comprobar el listado  anterior:

 

A nivel elemental es adecuado el uso de nuestro Buscador de Naturales

(http://www.hojamat.es/sindecimales/aritmetica/herramientas/herrarit.htm#buscador)

 

Se entiende fácilmente la condición impuesta.

Carácter multiplicativo

Para entender algunas cuestiones que seguirán, hay que recordar que las funciones SIGMA y TAU son multiplicativas, es decir, que en ellas se cumple la igualdad fundamental de este tipo de funciones, que es

F(a*b)=F(a)*F(b) si a y b son primos entre sí.

Puedes consultar la teoría de estas funciones en nuestra publicación “Funciones multiplicativas” (http://www.hojamat.es/publicaciones/multifun.pdf)

Se puede construir un pequeño esquema con Excel o Calc para comprobar esta propiedad:

 

Escribimos dos aritméticos primos entre sí y comprobamos que su producto también es aritmético.

Números primos y sus productos

Todos los números primos p mayores que 2 son aritméticos, ya que son impares, su función Sigma(p) equivale a 1+p, par, y su función Tau(p) es 2, luego su cociente es entero. Como consecuencia, según demostró Ore (O. Ore, On the averages of the divisors of a number, Amer. Math. Monthly 55

(1948), 615-619), todo número libre de cuadrados impar ha de ser aritmético, porque se puede aplicar la propiedad multiplicativa a todos sus factores primos. Como ejemplo, hemos repetido el esquema de más arriba usando productos de distintos primos:

 

Según lo anterior, los números semiprimos impares no cuadrados deberán ser aritméticos. Por ejemplo, 851=23*37

SIGMA(851)=SIGMA(23)*SIGMA(37)=24*38=912

y como TAU(851)=4, se cumple la definición al ser 912 divisible entre 4.

Aritméticos no libres de cuadrados

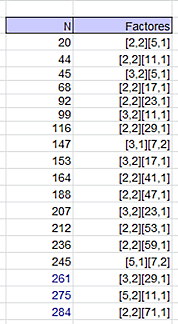
Existen muchos números aritméticos que no son libres de cuadrados. Uniendo las dos propiedades de ser aritmético y de poseer una parte cuadrada mayor que 1, resultan estos otros números:

20, 27, 44, 45, 49, 54, 56, 60, 68, 92, 96, 99, 116, 125, 126, 132, 135, 140, 147, 150, 153, 164, 168, 169, 184, 188, 189, 198, 204, 207, 212, 220, 224, 236, 245, 248, 260, 261, 264, 270, 275, 276, 280, 284, 294,…

Entre ellos hay cuadrados, cubos o productos de cuadrados por otros factores. Según se explica en la página https://oeis.org/A023883, algunos tipos de ellos se pueden identificar:

Cuadrados de primos del tipo 6k+1

Lo podemos comprobar fácilmente, pues el valor de TAU será 3, y SIGMA será:

(6k+1)²+6k+1+1=36k²+18k+3

Esta expresión es claramente un múltiplo de 3, luego el número es aritmético.

Los primeros ejemplos son:

49, 169, 361, 961, 1369, 1849, 3721, 4489, 5329, 6241, 9409, 10609, 11881, 16129,…

Cubos de primos impares

Los cubos de primos tienen cuatro divisores, y en el caso de impares resulta:

TAU(N)=(2k+1)³+(2k+1)²+2k+1+1=8k³+12k²+6k+1+4k²+4k+1+2k+1+1=8k³+16k²+12k+4, que es múltiplo de 4 y convierte en aritmético al cubo.

Primos del tipo 6k-1 multiplicados por  cuadrado de otro primo

La función TAU de p²q, siendo ambos primos será:

TAU(N)=TAU(p²)*TAU(q)=3*2=6

La función SIGMA vendrá dada por

(1+p+p²)(1+q)

y bastará con que sea q del tipo 6k-1 para que sea múltiplo de TAU.

En la tabla de los primeros casos de N=p²q observamos la abundancia de este tipo, de un primo al cuadrado multiplicado por otro q=6k-1.

 

 Números aritméticos primitivos

Vimos anteriormente que el carácter de aritmético tiene la propiedad multiplicativa, es decir, que el producto de dos números aritméticos coprimos es otro número aritmético.

Llamaremos números aritméticos primitivos a aquellos que no hayan tenido ese origen, que no sean producto de dos aritméticos coprimos mayores que 1.

Podemos identificarlos con una función para VBasic:

Function esprimaritmetico(n)

Dim i, a, r
Dim sigue As Boolean

If Not esaritmetico(n) Then esprimaritmetico = False: Exit Function
 ‘Si no es aritmético, no seguimos
sigue = True ‘Control de detención de la búsqueda
i = 2 ‘Posible divisor
r = Sqr(n) ‘Buscamos hasta la raíz cuadrada
While i < r And sigue ‘Bucle de búsqueda
If n Mod i = 0 Then ‘Es divisor
a = n / i ‘Posible factor aritmético
If esaritmetico(i) And esaritmetico(n / i) And mcd(i, n / i) = 1 Then sigue = False
 ‘Ambos aritméticos y coprimos
End If
i = i + 1
Wend
esprimaritmetico = sigue
End Function

Con esta función y un buscador cualquiera, identificamos los aritméticos primitivos. Los primeros son estos:

1, 3, 5, 6, 7, 11, 13, 14, 17, 19, 20, 22, 23, 27, 29, 31, 37, 38, 41, 43, 44, 45, 46, 47, 49, 53, 54, 56, 59, 61, 62, 67, 68, 71, 73, 79, 83, 86, 89, 92, 94, 96, 97, 99, 101, 103, 107, 109, 113, 116, 118, 125, 126, 127, 131, 134, 137, 139, 142, 149, 150, 151, 153, 157

Están publicados en https://oeis.org/A342438. Los hay primos y compuestos, pares e impares.

Los números primos han de ser necesariamente aritméticos primitivos, porque no son producto de dos factores mayores que 1.

Entre los números compuestos, según A342438, estarán los cuadrados de primos del tipo 6m+1. La razón es que son aritméticos, pues la suma de sus divisores es

36m²+12m+1+6m+1+1=36m²+18m+3, que es múltiplo del valor de TAU, que es 3.

Como, además, no son producto de dos factores coprimos, deberán ser aritméticos primitivos.

También serán de este tipo los cubos de primos impares.

Persistencia multiplicativa

Neil Sloane introdujo este término en su artículo [The persistence of a number, J. Recreational Math., 6 (1973), 97-98] En él define esta persistencia multiplicativa (existe otra muy popular, aditiva) de la forma siguiente:

Se multiplican las cifras del número (aquí sólo veremos las de base 10) y se reitera esta operación con los números obtenidos. Estos productos, como veremos, formarán una sucesión decreciente, y se cuentan las iteraciones necesarias hasta llegar a un producto de una sola cifra. Al número de esos pasos se le denomina índice de persistencia multiplicativa, y al número final resultante, raíz digital multiplicativa del número (existe otra raíz digital aditiva).

Lo vemos con un ejemplo: Iniciamos con el número 762. El producto de sus cifras es 84. Multiplicamos cifras de nuevo, resultando 32, y reiteramos:

762 – 84 – 32 – 6

El que los productos sean decrecientes es fácil de entender. Si el número es de una cifra, no hay producto y el índice lo definimos como 0. Si tiene dos cifras, sean a y b se tiene:

N=10*a+b>10*a>a*b, luego decrece.

Es fácil usar el mismo razonamiento cada vez que se añada una cifra:

100a+10b+c>10*10*a>a*b*c

Y así ocurrirá al ir añadiendo cifras.

Si uno de los productos posee una cifra 0, se terminará el proceso y su raíz digital valdrá 0. Paul Erdős sugirió ignorar los ceros en el producto, lo que daría lugar a procesos totalmente distintos.

Si dos números coinciden en sus cifras salvo en la cifra 1, tendrán la misma persistencia, como ocurre con 65, 165, 56111,... porque el producto de sus cifras es 30 en todos los casos.

Si dos números son anagramáticos (mismas cifras con la misma frecuencia) coincidirán también en sus resultados. Por tanto:

El proceso de persistencia es invariante al orden de las cifras y a la presencia de la cifra 1, con cualquier frecuencia.

Es fácil entender que el coincidir en la persistencia creará clases de equivalencia en los números naturales, e igual ocurrirá con los que coincidan en la misma raíz digital. Serán clases distintas, e incluso podemos considerar las clases en las que se coincida en los dos números, índice y raíz.

A continuación traduciremos todo esto a los procedimientos de las hojas de cálculo.

 Uso de una hoja de cálculo

Para estudiar este tema necesitamos varios procesos:

•    Extraer las cifras de un número dado

•    Proceder al producto de las cifras

•    Construir el algoritmo de iteraciones hasta llegar a la raíz digital

•    Expresión de los resultados, que pueden ser el índice de persistencia, la raíz digital o una cadena de texto que unifique ambos.

Procederemos por pasos.

Extracción de cifras

Este `proceso es habitual en nuestros trabajos. Existen varias técnicas, y hemos elegido esta:

Public Function cifra(m, n)

'Extrae la cifra n del número m si es natural. En caso contrario devuelve -1. También devuelve -1 si excede del número de cifras

Dim a, bIf esnatural(m) Then ‘Actúa sobre naturales
If n > numcifras(m) Then ‘La función numcifras se añadirá a continuación
cifra = -1
Else
a = 10 ^ (n - 1)
b = Int(m / a) - 10 * Int(m / a / 10) ‘Procedimiento de troceado de la cifra
cifra = b
End If
Else
cifra = -1
End If
End Function

Conteo de las cifras

Public Function numcifras(n)

Dim nn, a
'Calcula el número de cifras enteras de un número natural. Si no lo es, devuelve un cero
If esnatural(n) Then
a = 1: nn = 0
While a <= n
a = a * 10: nn = nn + 1 ‘Va multiplicando por 10 hasta llegar a n
Wend
numcifras = nn
Else
numcifras = 0
End If
End Function

Producto de cifras

Si poseemos una forma de extraer las cifras y otra de contarlas, construir su producto es fácil:

Public Function producifras(n)

Dim a, b, p, i
p = 1 ’Recogerá el producto
a = numcifras(n) ’Se cuentan las cifras
For i = 1 To a
p = p * cifra(n, i) ’Construcción del producto
Next i
producifras = p
End Function

Todas las funciones presentadas, aunque están escritas para VBasic, tienen traducción inmediata a otros lenguajes de programación.

Una vez que contamos con la función producto, es fácil organizar el proceso de persistencia. En un primer paso fijaremos que el resultado del proceso se nos devuelva en modo texto con todos los pasos y resultados. Para estadísticas cambiaremos el resultado o bien sólo al índice o a la raíz digital. La función correspondiente puede ser esta:

Cálculo de la persistencia

Function persistencia$(n) ‘Resultado en modo texto

Dim s$
Dim a, q
s = Str$(n) + ", " ‘Inicio del resultado
a = n ‘Variable que recoge el valor de n
q = 0 ‘Inicio del índice para números de una cifra
While numcifras(a) > 1
a = producifras(a) ‘Proceso de persistencia
s = s + Str$(a) + ", " ‘Incorporación al resultado
q = q + 1
Wend
s = s + "Índice: " + Str$(q) + " Raíz digital: " + Str$(a) ‘Creación del resultado
persistencia = s
End Function

Con esta función obtenemos el historial completo del proceso. En la siguiente tabla hemos elegido un intervalo de números al azar:

Se percibe un desequilibrio en los resultados. Es evidente la gran mayoría de resultados con raíz digital cero, pues la presencia de esa cifra detiene el proceso. Respecto a los índices, ninguno es mayor que 3. Escasean los índices mayores. Por ejemplo, el índice 11 no aparece hasta el número 10233.

Hemos construido una tabla de frecuencias para las raíces digitales del 0 al 9999, para hacer patente el desequilibrio entre ellas:

Aparte del caso del 0, es lógico que las frecuencias de 3 y el 7 sean tan pequeñas, pues muy pocos productos desembocarán en ellas. En el caso del

7, basta observar qué números desembocan en él:

17, 71, 117, 171, 711, 1117, 1171, 1711, 7111

También esta lista justifica el resultado del 9, porque todas las posibilidades de combinar la cifra 1 con la 7 son 2+3+4=9. Es fácil generalizar este resultado a más cifras.

Persistencia con potencias de cifras

El producto de cifras se puede construir con potencias de las mismas. Hablaríamos entonces de k-persistencia multiplicativa. Todos los números, salvo los “repunits”,1, 11, 111, …que tienen k-raíz digital 1, todos los demás poseen raíz 0. Lo hemos comprobado modificando nuestra función. Este hecho resta interés a este concepto.

 

Regresos 8 – Diferencia entre Catetos

En el año 2010 se publicó en este blog una entrada dedicada a los números

1, 7, 17, 23, 31, 41, 47, 49, 71, 73, 79 (https://hojaynumeros.blogspot.com/2010/10/1-7-17-23-31-41-47-49-71-73-79-primera.html), relacionados con las diferencias entre catetos en una terna pitagórica.

También se estudió el caso de los catetos consecutivos en tres entradas sobre “Oblongos y pitagóricos”

 (https://hojaynumeros.blogspot.com/2010/03/oblongos-y-pitagoricos-1.html y siguientes)

En estas entradas se llegó a que las diferencias entre catetos en ternas primitivas sólo pueden ser 1, 7, 17, 23, 31, 41, 47, 49, 71, 73, 79, 89, 97, 103, 113, 119, ...(http://oeis.org/A058529), que se caracterizan porque sus factores primos son del tipo p=8k+1 o p=8k-1.

Como en otras ocasiones, la disponibilidad de nuevas técnicas y herramientas nos lleva a regresar a ellos, ampliando el tema de las diferencias entre catetos. Damos algunas vueltas más a estas cuestiones.

Función para encontrar catetos con una diferencia dada

El primer paso para comprender el problema es tener en cuenta que lo que pretendemos es resolver esta ecuación para valores enteros positivos:

x²+(x+k)²=y²

Creamos una función de texto que devuelve las primeras soluciones respecto a k

function catetos_ligados$(k)
dim x,y
dim s$

x=3
s$=""
while x<500
y=x^2+(x+k)^2
if escuad(y) then ‘Es una solución
y=sqr(y)
s=s+"## "+str$(x)+", "+str$(x+k)+", "+str$(y)+" " ‘Se publica
end if
x=x+1
wend
if s="" then s="NO"
catetos_ligados=s
end function

Con esta función obtenemos los resultados para k=7

5,  12,  13
8,  15,  17
21,  28,  35
48,  55,  73
65,  72,  97
140,  147,  203
297,  304,  425
396,  403,  565

Si le pedimos tan solo el valor de x, resultará la sucesión

 5,  8,  21,  48,  65,  140,  297,  396,  833,  1748,  2325,  4872,  10205,  13568,  28413,  59496,  79097…

Esta sucesión coincide con la publicada en https://oeis.org/A076296

A076296              Consider all Pythagorean triples (X,X+7,Z); sequence gives X values.   

-3, 0, 5, 8, 21, 48, 65, 140, 297, 396, 833, 1748, 2325, 4872, 10205, 13568, 28413, 59496, 79097, 165620, 346785, 461028, 965321, 2021228, 2687085, 5626320, 11780597, 15661496, 32792613, 68662368, 91281905, 191129372, 400193625, 532029948, 1113983633

Esta sucesión posee infinitos términos, pues, según vimos en las entradas a las que regresamos, se cumple lo siguiente:

Si u y v engendran una terna pitagórica mediante las fórmulas 2uv, u²-v² y u²+v², los valores 2u+v y u engendran otra terna con la misma diferencia de catetos.

Así, el  primer ejemplo conseguido con diferencia 7, (5, 12,13) se ha generado con 3²+2²=13, 2*3*2=12 y 3²-2²=5, con lo que producirá también diferencia 7 el par de valores u=2*3+2=8 y v=3

Quedaría 8²+3²=73, 8²-3²=55 y  2*8*3=48, es decir, la terna (48, 55, 73), con diferencia entre catetos de 7, que figura en el listado.

Reiterando el procedimiento resultarían tantas ternas como deseáramos.

Estudio algebraico

Desarrollamos la ecuación correspondiente a la diferencia 7:

x²+(x+7)²=y²

2x²+14x+49=y²

4x²+28x+98=2y²

(2x+7)²+49=2y²

Si cambiamos de variable: u=2x+7, nos queda 2y²-u²=49

De esta forma se justifica la relación con los contenidos de las entradas referidas más arriba, porque tratamos con las soluciones de una ecuación del mismo tipo 2x²-y²=k, con lo que podemos aplicar lo que conocemos de ella.

Primera recurrencia

La ecuación 2x²-y²=k² la escribiremos mejor como x²-2y²=-k², para destacar que es del llamado tipo-Pell, pues puede basarse en esa famosa ecuación x²-Dy²=1, que tiene solución si D no es cuadrado perfecto (ver en este blog https://hojaynumeros.blogspot.com/2010/02/ecuacion-de-pell.html) y que es parecida a ella.

La ecuación que nos ocupa no es de ese tipo, por lo que su resolución es más complicada, pero existe una estrategia, si se dispone de una solución particular, para generar más soluciones (quizás no todas). Consiste en aplicar la recurrencia propia de la ecuación de Pell (aunque la que tratamos sea solo tipo-Pell), que copiamos de la entrada referida:

X_n+Y_n√D = (X_n-1+Y_n-1√D) (X₀+Y₀√D)

En este caso disponemos de la primera terna (5,  12,  13), y sabemos ya que si hacemos u=2x+7, se cumple que 2y²-u²=49, con lo que, cambiando la variable, X_n=2*5+7=17 e Y_n es la hipotenusa 13 de esa terna, y ambas cumplen 17²-2*13²=-49, luego (17, 13) es una solución particular (X_n,Y_n).

Ahora hay que tomar como (X₀,Y₀) una solución de la ecuación de Pell x²-2y²=1, que claramente puede ser (3, 2). Todo esto parece complicado, pero repasando se entiende. Resumimos:

(X_n,Y_n) es una solución de x²-2y²=-49, y podemos elegir el par (17,13)

(X₀,Y₀) es una solución de x²-2y²=1, y elegimos (3,2)

Según nuestra entrada referida, separando términos queda:

X_n = X_n-1X₀+Y_n-1Y₀D

Y_n = X_n-1Y₀+Y_n-1X₀

En nuestro caso

X_n = 3X_n-1+2*2Y_n-1

Y_n = 2X_n-12+3Y_n-1

Así podemos buscar otras soluciones a partir de 17 13.

Lo hemos intentado y resulta que nos devuelve todas las soluciones que deseemos, pero partiendo de X_n nos lleva a X_n+3. En la siguiente tabla lo destacamos:

La zona amarilla destaca las soluciones que no se obtienen por recurrencia. Las dos columnas centrales se han obtenido con la recurrencia explicada, a partir de (17, 13). El valor de X se obtiene de u=2x+7 o x=(u-7)/2, y el del otro cateto, restando 7 unidades a X.

Hemos comprobado que esta recurrencia nos devuelve más ternas, y se puede aplicar a cualquier otro valor de K.

Otros aspectos del problema

También se cumple que u²+7²=2y² por lo que u pertenece a https://oeis.org/A076293, ya que  la media cuadrática de los dos cuadrados, u² y 7² es entera. Esto ocurrirá en general, para un valor k adecuado de la diferencia: u²+k²=2y², con lo que u=2x+k siempre pertenecerá a esa sucesión.

Si nos limitamos a ternas pitagóricas primitivas, un cateto podría representarse com u²-v² y el otro como 2uv, según un procedimiento muy conocido. En este caso, salvo quizás el signo, se cumplirá que u²-v²-2uv=k, o bien:

(u-v)²-2v²=k

Según las propiedades de estas ternas, las bases de los dos cuadrados han de ser de distinta paridad y números primos entre sí. Por eso k ha de ser impar. Esto justifica el que los valores de k posibles han de pertenecer a la sucesión 1, 7, 17, 23, 31, 41, 47, 49, 71, 73, 79,…pues estos son las soluciones de la ecuación x²-2y²=k, similar a la obtenida con cambios de variables adecuados. En https://oeis.org/A058529 se explica su propiedad de tener sólo factores primos del tipo 8k+1 o del 8k-1.

Una propiedad interesante derivada de todo lo anterior es que si un valor de k es válido para ser diferencia de catetos, también los es k², porque ambos son soluciones de una ecuación del tipo x²-2y²=k. Lo hemos comprobado con la función catetos_ligados. En la imagen se refleja esta propiedad en el caso de k=71:

 

Segunda recurrencia

En OEIS A076296 se propone una ecuación de recurrencia para los valores X del cateto menor en el caso ya estudiado de k=7. Es esta:

 a(n)=6*a(n-3)-a(n-6)+14.

La hemos comprobado con nuestra herramienta ecurrecurre (ver  listado de herramientas para el blog en http://www.hojamat.es/sindecimales/otros.htm) en el apartado de recurrencias no homogéneas.

En esta captura de pantalla se pueden comprobar los coeficientes 6, -1, 14

 

Hemos copiado los términos de tres en tres.

Este resultado nos anima a probar cono otros valores posibles de k. El siguiente es 17. En primer lugar, hemos creado la sucesión de lados de las ternas usando nuestra función para VBasic:

##  7,  31,  25 ##  28,  73,  53 ##  51,  119,  85 ##  88,  193,  137 ##  207,  431,  305 ##  340,  697,  493 ##  555,  1127,  797 ##  1248,  2513,  1777 ##  2023,  4063,  2873 ##  3276,  6569,  4645 ##  7315,  14647,  10357 ##  11832,  23681,  16745 ##  19135,  38287,  27073 ##  42676,  85369,  60365

A continuación hemos seleccionado los catetos menores de tres en tres (los que aparecen en negrita). Los hemos volcado como datos en ecurrecurre, eligiendo el caso de “No homogénea”. El resultado confirma nuestra intuición. Se mantienen los coeficientes y el término independiente resulta ser 2k, como en el caso de k=7:

 

No es de extrañar el valor de 34, ya que, en realidad, todas estas sucesiones están ligadas con https://oeis.org/A076293, que contiene los valores de 2x+k, según vimos más arriba. En esta sucesión la recurrencia es homogénea: a(n)=6a(n-3)-a(n-6), según hemos comprobado también. Por eso se produce un desfase entre ambas sucesiones, que se traduce en el término independiente 2k.

Sea x(n)=(a(n)-k)/2. Podemos manipular la ecuación de recurrencia:

a(n)-k=6(a(n-3)-k)-(a(n-6)-k)+4k

(a(n)-k)/2=6((a(n-3)-k)/2)-(a(n-6)-k)/2+2k

Y queda x(n)=6x(n-3)-x(n-6)+2k

Hemos demostrado que los valores de X para cualquier valor de k se pueden encontrar mediante la recurrencia a(n)=6a(n-3)-a(n-6)-2k, basándonos en que los términos de https://oeis.org/A076293 se generan con esta otra: a(n)=6a(n-3)-a(n-6).