Si no lo pensaste al leer la entrada anterior, ahí van dos propuestas:
Elemental
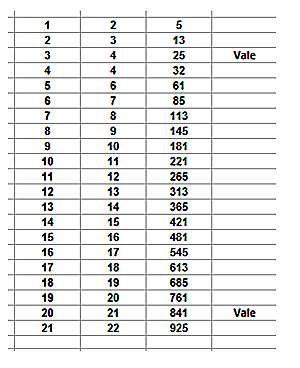
Rellena una columna con los primeros números naturales consecutivos, y en la columna de su derecha auméntalos en una unidad. Supongamos que has comenzado en las celdas B4 y C4 respectivamente. En ese caso puedes rellenar la celda D4 con la fórmula B4^2+C4^2, y en la E4 una condición que nos devuelva la palabra “Vale” si es cuadrado perfecto:
SI(D4=(ENTERO(RAÍZ(D4))^2; “Vale”;””).
Si usas Excel suprime la tilde de la palabra RAIZ. De esta forma descubriremos las soluciones, con algo de paciencia, tiempo y muchas filas de hoja de cálculo:
Con Basic
La misma idea de construir una lista para X, otra para X+1 y una tercera en la que buscamos los cuadrados perfectos se puede construir en Basic. X lo almacenamos en la variable i, X+1 en la j, y la hipotenusa en k. Una sentencia IF nos presenta las soluciones en las que k es un entero.
Con este código se buscan las soluciones para números inferiores a 1000000.
Sub busquedas
Dim i,j,k
for i=1 to 1000000
j=i+1
k=i^2+j^2
if k=Int(sqr(k))^2 then
msgbox(i)
msgbox(j)
msgbox(sqr(k))
end if
next i
End Sub
Otro día nos pondremos más serios e intentaremos un estudio algebraico. Si te quieres adelantar…
2 comentarios:
Muy práctica la aplicación, me acordé de mis tiempos de universitario, cuando aprendí a programar en BASIC.
En el ramo de métodos estadísticos necesitábamos resolver ecuaciones y ya estaban apareciendo unas calculadoras que resolvían todo, pero, para suerte mía, no me alcanzaba la plata.
Finalmente me compré una mucho más simple y que soportaba BASIC, y en un libro de "matemáticas especiales para computación" (de García Valle) aparecían tres métodos de aproximación, que consisten en ideas similares a la que muestras aquí.
Me acuerdo de dos ellos, el de "Biyección sucesiva" (o del punto medio) y el de "Newton Raphson", que tenía que ver con la recta tangente.
Aunque en tan básica calculadora la resolución típica demoraba unos minutos (ese "for" hasta 10^6, demoraría horas) , gracias a esta limitante aprendí a programar y para mí eso es lo más interesante que enseño en estos días.
En fin, me gustó cómo presentan esta idea, porque la hoja de cálculo debe ser una excelente herramienta para "rutear" un programa.
Saludos :)
Gracias por tu comentario
Yo también he tenido una larga historia con las calculadoras programables y el Basic. Ahora me limito a las hojas de cálculo y a los números, pero recuerdo también el "Newton Raphson" :) que era un método muy rápido de aproximación.
Saludos
Publicar un comentario