Define tus propias funciones en OpenOffice.org Calc

En ocasiones desearás definir otras funciones además de las que OpenOffice.org Calc te ofrece. Por ejemplo, sería útil una función tal que si se aplica a un número entero positivo devuelva su mayor divisor. Para ello disponemos del lenguaje Basic (de macros) que lleva incorporado Calc. 

A partir de esta entrada iremos explicando en otras sucesivas la forma de implementar algunas funciones. Antes de nada hay que aprender a definirlas en el Editor de Basic.

Editor de Basic

Crea una hoja o abre alguna existente. Para abrir el editor sigue la secuencia: Menú Herramientas > Macros > Organizar macros > OpenOffice.org Basic.

Si es la primera función que defines, busca la carpeta correspondiente al nombre de tu hoja de cálculo (si lo acabas de crear, se llamará Sin Nombre o Sin Título). No señales la otra carpeta Standard, que es más general. Si ya has definido algunas funciones, habrás definido un módulo contenedor. Abre ese módulo.

Si no habías creado ningún módulo, una vez elegida la carpeta, pulsa el botón Nuevo para abrir un nuevo módulo contenedor. Se te ofrecerá el nombre de module1, module2 u otro similar. Acepta el nombre o cámbialo según tu criterio. Al aceptar el nombre se abrirá el editor de macros. Por defecto aparecerá la macro Main, que puedes borrar o ignorar.

Escritura del código

Terminada la secuencia anterior, borra lo que esté escrito de la macro Main y escribe el código de una función:

Debes comenzar con

Function nombre de la función ( argumento )

y terminar con

End function

y entre ambas, el código de la función. En ese código debemos usar el nombre de la función seguida del signo igual y de su definición

Es mejor verlo con un ejemplo:

Function cubo ( numero )

cubo=numero*numero*numero

End function

En el ejemplo, el nombre de la función es cubo, y su argumento numero (lo traduciríamos como "Cubo de un número")

Después volvemos a escribir cubo, el signo igual, y su definición.

Uso de la función

Una vez escrito el código, cierra el Editor de Basic y usa tu función en cualquier celda. En la imagen puedes ver que en B2 se ha escrito un número y en B4 la fórmula =CUBO(B2)

Con esto ya tienes definida la función. 

Con la técnica explicada, esa función sólo estará activa en la hoja de cálculo en la que la has creado, no en otras. Al cerrar la hoja ya no podrás usarla. 

(Continuará)

Resolución con dos teclas

Intentemos resolver el siguiente problema con calculadora u hoja de cálculo:

Encontrar varios números naturales consecutivos cuyo producto sea igual a un número natural N dado.

(a) Con dos números es inmediato: Si sabemos con seguridad que la ecuación x(x+1)=N tiene soluciones enteras, como sería x(x+1)=132, es posible encontrar la solución de la ecuación con las teclas de raíz cuadrada y parte entera. En la hoja de cálculo se usaría =ENTERO(RAÍZ(N)) (En Excel escribe RAIZ sin tilde)

En efecto ENTERO(RAÍZ(132))=11, que es la solución de x(x+1)=132, pues 11*12=132.

La razón de que esto funcione es la desigualdad

 También funciona este procedimiento para x(x+1)(x+2)=N. Así,  la solución de x(x+1)(x+2)=13800 es la parte entera de su raíz cúbica, que en hoja de cálculo se expresaría como =ENTERO(N^(1/3)), y en el ejemplo nos daría la solución 23, y comprobando, 23*24*25=13800.

La razón aquí es una desigualdad similar a la anterior

 

Esta no es trivial. Razónala si así lo deseas.

¿Ocurriría lo mismo con cuatro números consecutivos? Pues no exactamente, pues necesitarías dos teclas y algo más. Quizás el siguiente desarrollo te dé una idea, pero razona o demuestra todo con rigor, que hay alguna dificultad.

En vista de esto, podíamos intentar procedimientos similares para cinco o seis números. Inténtalo, y que no te pierdas con tanto polinomio

Combinado de murciélago

La palabra MURCIELAGO ha sido usada tradicionalmente para la codificación en pequeños comercios, por tener diez letras distintas (5 vocales y 5 consonantes) que se pueden usar para representar las cifras de 0 a 9 en una asignación decidida por cada comerciante: M=0, C=1, E=2, etc.

Sobre ella se pueden plantear muchos problemas de distintos niveles. Aquí hemos elegido unos cuantos:

(a) ¿De cuántas formas se pueden ordenar las letras de MURCIELAGO, de forma que no caigan todas las vocales seguidas? (Se prohíben permutaciones como MRCOAEIULG)

(b) ¿Y si deseamos que nunca aparezcan vocales consecutivas, aunque sólo sean dos? (Deseamos que todas estén separadas)

(c) ¿Y si, por el contrario, deben estar las cinco vocales consecutivas y en su orden natural?

Se pueden inventar más, pero la Combinatoria cansa mucho. Suerte con ellos.

El mayor divisor

Es fácil demostrar que todo número M que venga dado por la expresión 2ⁿ-1 con n natural compuesto, es también compuesto. Lo que no es tan inmediato es calcular su mayor divisor propio. Por ejemplo, el mayor divisor de 2²⁰-1=1048575 es 349525.

¿Qué protocolo de cálculo podríamos seguir para encontrar el mayor divisor de 2ⁿ-1 (n compuesto) con un número pequeño de pasos? No es exactamente un algoritmo, sino una estrategia. Para números grandes se puede complicar, pero para n menor que 100 no debería darnos problema.

Aquí puedes estudiar algunos resultados con valores de n compuestos:

Dos demostraciones propuestas por T. M. Apostol

En el libro “Introducción a la Teoría analítica de números” de T. M. Apostol hemos encontrado dos propuestas de demostración de nivel medio sobre números primos y compuestos:

(a) Demostrar que todo número N mayor que 12 es suma de dos compuestos.
(b) Demostrar que si 2ⁿ+1 es primo, n ha de ser potencia de 2.

En la primera has de darte cuenta del papel que juega el número 12. Quizás debas expresar el número N en forma de binomio.

La segunda recuerda los números de Fermat. Un camino posible es el de abordar el teorema recíproco.

No son excesivamente difíciles.

Un cuadrado más una unidad

Los números de la forma n²+1 con n natural tienen un atractivo especial: un cuadrado que se estropea por añadirle un elemento más. ¿Qué hacer con esta figura? A veces da lugar a un número primo, como 17, 37 o 101, y otras a un compuesto, como 50 o 26 Este es el de la figura, que se puede convertir en un rectángulo de 2 por 13.

Lo que es seguro es que estos números nunca serán múltiplos de 3, ni de 4, y tampoco de 7, pero sí pueden serlo de 17 (13^2+1=170=17*10) o de 13 (21^2+1=442=13*34)

¿De qué depende eso? Puedes abordarlo sin especiales conocimientos de teoría de números, con el uso de una hoja de cálculo. Si prefieres profundizar, te servirá de ayuda saber que esto está relacionado con los restos cuadráticos.

La tabla misteriosa

La tabla misteriosa

En esta tabla están casi todos los primeros números naturales. Lo que ves es sólo un fragmento de otra mayor que puede tener tantas filas y columnas como deseemos.

(1) ¿Cómo se ha generado esta tabla? Si lo descubres (no es difícil) tendrás las demás respuestas casi resueltas.

(2) En esta tabla no están todos los primeros números. ¿Cuáles faltan? ¿Qué característica comparten? (no cuentes el 1, que es un caso especial)

(3) Por el contrario, algunos de ellos están repetidos. Si prolongásemos la tabla se incrementarían las repeticiones. ¿Qué clase de números están repetidos?

(4) Todos los números de la primera columna se pueden expresar como k(k+2), siendo n natural. ¿Admiten expresiones similares las restantes columnas?

(5) Los números de la misma fila pueden descomponerse en factores del tipo n(k-n), siendo n y k naturales y k constante para la misma fila. ¿Puedes concretarlo más?

(6) ¿Qué podemos afirmar de las diagonales descendentes? La primera está formada por impares, la segunda por múltiplos de cuatro, y, en general, todas son sucesiones aritméticas ¿Por qué?

Ya sabes, acertando la primera, las demás caerán fácilmente.

Conjuntos numéricos idénticos

En algunas cuestiones resulta útil decidir de forma automática si dos conjuntos numéricos son idénticos o no. Por ejemplo, en las tablas de multiplicar de los cuerpos finitos, como Z/Z7, es interesante descubrir si

(a) No existen elementos repetidos en ninguna fila o columna

(b)  Los elementos de las distintas filas son los mismos.

Si escribimos los dos conjuntos en una hoja de cálculo, en filas paralelas, deberemos comprobar cuatro hechos para decidir si los conjuntos son idénticos o no:

 (1)   No existen elementos repetidos en el primer conjunto 

(2)   Tampoco se repiten los del segundo

(3)   Todo elemento del primero ha de pertenecer al segundo

(4)   Todo elemento del segundo ha de pertenecer al primero.

 

Las cuatro cuestiones las resuelve la función CONTAR.SI. Recorremos todo el primer conjunto y mediante esta función contamos las veces que figuran en el segundo. Si esos valores son mayores que 1, es que existen repetidos en el segundo conjunto, y si es 0, es que falta alguno. Lo deseable, pues, es que todos los contadores presenten el valor 1. 

Procedemos de la misma forma, contando las veces que los elementos del segundo conjunto figuran en el primero, y también han de valer 1. Para evitar problemas en las siguientes operaciones que explicaremos, a las celdas vacías también se le debe asignar un 1.

¿Cómo resumimos la situación? Multiplicamos todos los contadores del primer conjunto, y nos ha de resultar la unidad. Ocurrirá lo mismo con el producto de los del segundo, por lo que si multiplicamos ambos productos, obtendremos un criterio para decidir si los dos conjuntos son idénticos: el que el producto final tenga el valor de 1.

Puedes estudiar este proceso en los apuntes interactivos contenidos en http:/www.hojamat.es, en concreto la hoja grupos.ods.

Ver y calcular (1)

El estudio de cuestiones aritméticas deriva pronto a cálculos algebraicos, generalmente tediosos, y, en algunos casos, también a esquemas geométricos. Estos dos caminos, el algebraico y el visual se complementan perfectamente. Los números figurados, por su propia definición, son buenos elementos de unión entre ellos. Veamos un ejemplo cn números triangulares:

“Llamamos T(n) al enésimo numero natural. ¿Qué obtenemos si sumamos los cuadrados de un número triangular T(n) y de su siguiente T(n+1)?

Orientación algebraica

Conjetura: Diseñamos una tabla de números triangulares en una hoja de cálculo y en una columna adjunta calculamos la suma de cuadrados pedida para todos los casos posibles. Fácilmente se descubre una ley de formación. No indicamos el resultado, tan sólo que es un número triangular. ¿Cuál?

Cálculo: Mediante cálculos algebraicos se puede verificar la conjetura. Basta desarrollar la expresión y comprobar su resultado con el imaginado. En la imagen tienes un desarrollo efectuado con la calculadora Wiris. La conjetura está un poco escondida.

Orientación geométrica

Podemos atrevernos a pensar que si T(n) es un número triangular, su cuadrado se podrá representar por otro número triangular idéntico a él, pero sus elementos no serán puntos o bolitas, sino triángulos más pequeños. Sería “un triángulo de triángulos”.

Si no acertaste la conjetura por medio del Álgebra, esta imagen te la sugerirá con más facilidad. Las bolitas rojas corresponden al cuadrado de T(4) y las verdes al de T(3). Si no sientes una pequeña emoción al analizarla es que no te gustan de verdad las Matemáticas.

Grandes periodos

¿Cuál es el periodo de la fracción 77/23?

Las hojas de cálculo están orientadas a los números decimales y se comportan mal en algunos problemas que necesitan operaciones con números enteros. Así, en la cuestión de obtener el periodo de una fracción, aunque es un problema propio de números racionales, los cálculos se efectúan mediante la división entera tradicional. Así se efectuaba en las aulas cuando no existían las calculadoras.

No es difícil implementar una división entera para obtener los periodos largos que se producen con denominadores que contengan como factores números primos grandes. La idea es usar las funciones COCIENTE y RESIDUO de OpenOffice.org Calc ( Excel no usa la función COCIENTE, pero se puede sustituir por ENTERO(numerador/denominador)).

Por ejemplo, para obtener muchas cifras decimales del cociente 77/23, podemos proceder así: El cociente entre ambos sería COCIENTE(77;23) = 3 (En Excel ENTERO(77/23), que sería la parte entera. El resto se hallaría mediante RESIDUO(77;23)=8. 

A continuación podemos imitar la división que efectuábamos en el colegio (“sacar decimales”). Podemos multiplicar el resto 8 por 10 y volver a repetir la operación: COCIENTE(80;23) = 3, que sería la primera cifra decimal. Volvemos a hallar el resto: RESIDUO(80;23) = 11. Y así reiteramos cuantas veces deseemos.

En la imagen puedes estudiar la forma de ordenar estos cálculos

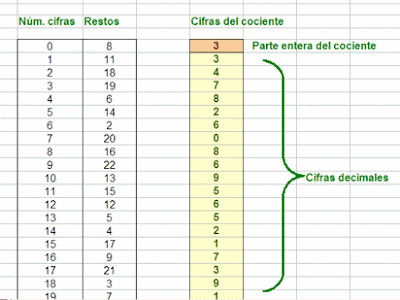
Puedes profundizar en este algoritmo en el archivo de dirección

http://www.hojamat.es/sindecimales/aritmetica/teoria/hojas/granperiod.ods

(Si usas Internet Explorer, el programa puede interpretar como archivo .zip la hoja de cálculo de OpenOffice) 

Versión en Excel: 

http://www.hojamat.es/sindecimales/aritmetica/teoria/hojas/granperiod.xls

¿En qué terminan los números triangulares?

Ideas para una webquest

“Los números triangulares, expresados en base decimal, no pueden terminar en 2, 4, 7 ó 9”

La metodología de las webquest se adapta muy bien al uso de las hojas de cálculo y a una buena atención a la diversidad. La afirmación anterior constituye un punto de partida que admite la organización de una webquest con distintos itinerarios de aprendizaje según los niveles del alumnado.
Se puede comenzar con la frase de arriba, y organizar una webquest para entender bien su significado y los fundamentos de esa afirmación. Incluimos a continuación algunos pasos que se podrían seguir:

(a) Definición de número triangular

Se puede buscar en páginas fiables, tales como Wikipedia o la misma Hojamat del autor de esta entrada.

(a1) Para el alumnado más aventajado, se sugerirá alguna búsqueda de carácter histórico sobre estos números.
(a2) Los estudiantes con dificultades pueden copiar imágenes de números triangulares y pegarlas en un documento.

(b) Fórmula de los números triangulares

Lo ideal sería que se pudiera deducir en el aula esta fórmua mediante inducción y discusión en grupos con la ayuda del profesorado. Así lo ha conseguido el autor en varias ocasiones, Si no, en las mismas páginas se puede encontrar dicha fórmula.

Una vez conseguida la fórmula T(n)=n(n+1)/2, se construye una tabla de números triangulares con una hoja de cálculo.

(b1) Este paso admite una rama de profundización consistente en buscar en la red propiedades de los números triangulares y experimentarlas con la misma hoja de cálculo. También se puede intentar generarlos por recurrencia: T(n+1) = T(n)+n+1
(b2) Una rama de consolidación del aprendizaje consistiría en aplicar esa fórmula sin el uso del ordenador y reproducir en papel las operaciones que se han efectuado en la hoja de cálculo.

(c) Terminación de los números triangulares

Ya se está en condiciones de comprobar que ningún número triangular termina en 2, 4, 7 ó 9, y, lo más importante, intentar justificarlo mediante la fórmula o razonamiento. Mediante la fórmula T(n)=n(n+1)/2 se puede discutir en qué cifra puede terminar n, después n+1, su producto y, por último, la mitad del mismo. Una tabla de hoja de cálculo podría ser muy útil.

(c1) Una actividad de perfeccionamiento consistiría en usar la propiedad de que “si tomo ocho veces un número triangular y después sumo 1, resulta un cuadrado”. Se estudian las terminaciones de los cuadrados impares, se les quita una unidad y se discute su cociente entre 8.
(c2) Para el alumnado que necesite consolidar lo aprendido, se puede organizar el cálculo de números triangulares grandes para comprobar sus terminaciones.

(d) Presentación de resultados

Todo el trabajo realizado se expone al resto del aula mediante documentos, presentaciones o puestas en común. Si se dispone de una web de centro, se incluye en ella todo el material generado en la webquest.

Con estas ideas, adaptándolas al nivel y características de vuestros estudiantes, podéis diseñar una o dos sesiones de trabajo que pueden resultar interesantes.

Cuadrados en progresión aritmética (II)

Tal como prometimos, intentaremos un análisis algo más profundo sobre el tema de encontrar ternas de cuadrados perfectos que estén en progresión aritmética, tales como 1, 25 y 49, o 4, 100 y 196.

Esto nos da un procedimiento de generación de ternas de cuadrados: Elegimos cualquier entero p y buscamos un número par h cuyo cuadrado sea divisible entre p, y mediante la fórmula (1) calculamos n

Ejemplo: p=5, h=10, n=100/10 + 10 + 5 = 25; (n+h)=35: (n-k)=25-10-5*2=5.

Por tanto, los cuadrados en progresión aritmética buscados son: 25, 625 y 1225.

En la imagen inicial puedes observar una tabla que genera ternas de este tipo de forma sistemática

¿Se te ocurre otro análisis del problema?

Cuadrados en progresión aritmética (I)

No es difícil encontrar ternas de cuadrados perfectos que estén en progresión aritmética, tales como 1, 25 y 49, o 4, 100 y 196. ¿Cómo podríamos encontrar más ternas con una hoja de cálculo? Se podría organizar una tabla de doble entrada con los cuadrados perfectos, y después someter a su media aritmética a una condición ¿Cuál?

En la imagen puedes ver el resultado de una búsqueda similar, en la que se han marcado con un 1 los cuadrados perfectos pertenecientes a una terna como la propuesta. Si te animas a construir un buscador semejante podrás encontrar muchas más ternas. Ponte a prueba: ¿Con qué otros dos cuadrados forma progresión aritmética el número 10404, cuadrado de 102? Si lo encuentras, nos lo puedes comunicar en forma de comentario.

Para concretar las ternas pedidas hemos recurrido a una exploración sistemática. Es una forma válida de trabajar en Matemáticas (así se encuentran los números primos), pero que alguien puede pensar que es algo perezosa. Podríamos aportar un análisis algo más profundo, pero eso será en una próxima entrada.