En septiembre de 2009 publiqué dos entradas sobre números que se pueden expresar como combinatorios de varias formas. Se transcriben a continuación algunos párrafos de ellas.
Todo número natural m se puede expresar como un número combinatorio,
porque
Sólo una proporción pequeña de números admite otra representación (o varias) en forma de número combinatorio. Así el 6 admite tres representaciones
El número 35 admite cuatro
Los números 120 y 210 admiten seis representaciones. Aquí tienes las de 120:
No hay muchos más números entre los 10000 primeros que presenten representaciones con tantas posibilidades. Sin embargo, existe un número de cuatro cifras, capicúa, que se puede representar de ocho formas diferentes. Es el número 3003, porque
Este tipo de cuestiones se pueden abordar con hoja de cálculo de varias formas.
Estudio
sin macros
Para encontrar expresiones
de un número como combinatorio no trivial (excluyendo C(n,0), C(n,1), C(n,n-1)
y C(n,n), cuyos valores se encuentran de inmediato), se puede formar el
triángulo de Tartaglia o Pascal en una hoja de cálculo y después buscar en la
matriz correspondiente el número que nos interesa.
Una cuestión previa es la de
saber hasta qué fila del triángulo se debe considerar, de forma que en las
siguientes no encontraremos el número buscado N. Una idea sencilla es la de que
en la fila k el número combinatorio más pequeño es C(k,2)=k(k-1)/2. Si
igualamos a N tendremos un tope para las filas a considerar, porque en las
siguientes los combinatorios serán mayores que N.
Despejamos y resulta:
2N=k(k-1); luego (k-1)2<2N. Esto nos
proporciona una cota para los valores de k. Tomamos parte entera y añadimos una
unidad:
Para explorar los números
combinatorios puedes usar las hojas de cálculo contenidas en la página http://www.hojamat.es.
(Ver en el apartado de Herramientas de Combinatoria, la dirección http://www.hojamat.es/sindecimales/combinatoria/herramientas/hoja/tartaglia.xls)
Fijamos el número a buscar, por ejemplo el 210. Deberemos seleccionar el
triángulo hasta la fila INT(RAIZ(210*2))+1=21. En la imagen sólo se incluye
parte del triángulo:
Encontramos 210 en la fila
21 (no se ve la otra solución) y en la fila 10, luego es un número
multicombinatorio.
Si hay que usar muchas
filas, se puede seleccionar todo el rango del triángulo y asignarle el nombre
de tartaglia. Luego, con la función =CONTAR.SI(tartaglia;210) se
buscan las veces en las que aparece el 210 u otro número cualquiera que desees
probar. Incluso puedes escribir los números en columna y aplicar la fórmula
reiteradamente.
Con este procedimiento puedes encontrar otros números multicombinatorios, como
1540 o 7140, ...
Sus descomposiciones en
factores primos nos pueden dar una pista del porqué de su propiedad.
120= 2*2*2*3*5; 210=2*3*5*7; 1540=2*5*7*11; 3003=3*7*11*13; 7140=2*3*5*7*17
La gran variedad de su factores primos hace que estos números puedan aparecer
en cocientes de factoriales, como los usados en los números combinatorios.
Mediante
una función
Se puede organizar una búsqueda si se posee una función sobre un número N, tal
que nos devuelva todas las formas de ser combinatorio que posee ese número.
Uso
de la función COMBINAT
Podemos usar también la
función de las hojas que nos da un número combinatorio, COMBINAT(N;K). Para
cada número N a probar se organiza un bucle doble para el
índice superior m del número combinatorio y para k el
inferior. El índice m recorrerá los valores entre 1 y el tope. El índice k recorrerá
todos los valores hasta que el número combinatorio iguale o sobrepase a N.
Para cada valor concreto de N se cuentan las veces en las que
los valores m y k producen un número
combinatorio igual a N y se
devuelven en modo texto para posteriores operaciones. No se tienen en
cuenta los casos triviales con índices inferiores 0, 1, n-1 y n.
Una versión de esta función
puede ser:
Function escombi$(n) ‘No
se incluyen C(n,0) ni C(n,1)
Dim i, k, v, m As Double
Dim s$
m = Int(Sqr(2 * n) + 1) ’Un
tope razonable
For i = 3 To m ‘Índice
superior. Se excluyen 1 y 2
For k = 2 To i – 2 ‘Índice
inferior, sin 0, 1, n-1 y n
v =
Application.WorksheetFunction.Combin(i, k)’Número
combinatorio
If abs(v – n)<1e-6 Then s
= s + " (" + Str$(i) + " , " + Str$(k) + ")"’Nueva
solución. No se usa v=n por los redondeos
Next k
Next i
If s = "" Then s =
"NO"’ Si no es combinatorio devuelve un NO
escombi = s
End Function
Se ha tenido que usar el criterio abs(v-n)<1e-6 porque combin no da siempre un entero bien definido cuando crece demasiado el índice superior.
Con esta función se
descubren los números combinatorios no triviales. Por ejemplo, entre 10 y 21
obtendríamos:
Siempre encontraremos
una mayoría que no es un número combinatorio, y obtendremos un “NO”. Serán
frecuentes los números triangulares, que son de la forma C(n,2), que aquí
serían 10, 15 y 21. En la tabla aparece también el 20, que es C(6,3).
Podemos buscar combinatorios en cualquier rango, tal como hemos procedido en la siguiente tabla:
Observamos que la
mayoría de soluciones son números triangulares, que son aquellos en los que el
índice inferior puede valer 2. Figura el ejemplo de 120 que usamos
anteriormente.
Están publicados en https://oeis.org/A006987, y su programación en PARI coincide básicamente con nuestra función en VBasic.
Algoritmo sin la función COMBINAT
La función COMBINAT puede presentar errores porque se sobrepase en los cálculos la capacidad de los registros o por redondeo de decimales. Es mucho más rápida la construcción de los combinatorios por filas del triángulo de Tartaglia, basándonos en estas cuatro identidades:
Como las dos primeras no nos interesan, comenzaríamos la búsqueda en C(n, 2), y a partir de ella generaríamos combinatorios hasta el centro de la fila del triángulo, para ignorar el combinatorio simétrico. La función quedaría así:
Function escombi$(n)
Dim i, k, v, m As Double
Dim s$
s = ""
m = Int(Sqr(2 * n) + 1)’Filas
del triángulo de Pascal
For i = 3 To m
k = 2: v = i * (i - 1) / 2’
Se comienza por C(i,2)
While k <= Int(i / 2) And
v <= n’ Solo se llega a la mitad de la fila y se
ignora el simétrico
If v = n Then s = s + "
(" + Str$(i) + " , " + Str$(k) + ")"
v = v * (i - k) / (k + 1) ‘Siguiente
número combinatorio de la fila
k = k + 1
Wend
Next i
If s = "" Then s =
"NO"
escombi = s
End Function
Este planteamiento es más rápido que el anterior, y da más seguridad en la exactitud de los cálculos. En la siguiente tabla figuran los mismos resultados, sin las soluciones simétricas:
Aquí destacan más los
multicombinatorios como el 120.
Otras posibilidades
La función que hemos presentado se puede convertir en booleana, que sus salidas sean VERDADERO y FALSO. De esa forma sería sencillo plantear otras cuestiones, que las dejamos como ejemplo:
Con esta función en modo booleano es fácil encontrar números combinatorios cerca de un número dado. Podríamos diseñar funciones del tipo SIGUIENTE o ANTERIOR. Así, el número combinatorio que sigue al 4000 sería
SIGUIENTE(4000)=4005=C(90,2)
El anterior a 10000
es
ANTERIOR(10000)=9980=C(40,3)
Podríamos, igualmente, encontrar números combinatorios que también fueran cuadrados, como el 4, el 36 o el 1225. Otros números que fueran promedios de combinatorios… y así podríamos seguir.
En otro ámbito, hemos aplicado un algoritmo voraz para descomponer (salvo algún resto) un número en sumandos combinatorios. Por ejemplo:
22324=C(211,2)+C(11,3)+C(4,1)
Nos podemos plantear otras tareas, que quedan pendientes para algún otro momento.






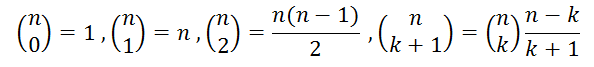

No hay comentarios:
Publicar un comentario