En la anterior entrada hemos supuesto que el número de sumandos en una partición era libre, hasta el mayor posible. Puede ocurrir, sin embargo, que sólo deseemos usar un máximo de hasta tres sumandos, o exactamente cuatro o cualquier otra posibilidad. Por otra parte, los sumandos pueden estar restringidos en magnitud dentro de un rango. Esto complica un poco las cuestiones.
Veremos con algunos ejemplos la utilidad de las funciones generatrices y la posibilidad de comprobar resultados con la hoja Cartesius.
¿De cuántas formas se puede descomponer el número 8 en sumandos no mayores que 4?
Si has entendido de qué van las funciones generatrices comprobarás que la siguiente es la adecuada para este caso
Como en casos anteriores podemos expresarlo como sumas de sucesiones geométricas
Y en general
Para aplicarlo al caso de 8 bastará buscar su coeficiente en la F.G. aplicada al caso en el que k=4. Lo escribimos en PARI
print(taylor(1/(1-x)/(1-x^2)/(1-x^3)/(1-x^4),x,9))
Y obtenemos
F.G.=1+x+2x^2+3*x^3+5*x^4+6*x^5+9*x^6+11*x^7+15*x^8+O(x^9)
Luego la solución del problema es P(8/sumandos no mayores que 4)=15
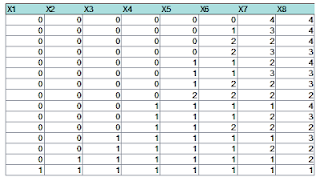
Si lo planteamos con Cartesius obtenemos los 15
Particiones conjugadas
Ahora usaremos una técnica muy simple, pero que da buenos resultados. Como veíamos en otra entrada (http://hojaynumeros.blogspot.com.es/2011/02/particiones-de-un-numero.html) cada una de las particiones se puede representar mediante un diagrama de Ferrer, en el que se adosan tantas filas como sumandos entran en la partición, siendo la longitud de cada columna el valor del sumando. Así, la partición 8=4+2+1+1 se puede representar como
Cada fila representa un sumando: 4, 2, 1 y 1. Todos los diagramas que formemos con estas 15 particiones tendrán como máxima anchura cuatro cuadrados.
Lo bueno de estos diagramas, entre otras ventajas, es que si los giramos convirtiendo las filas en columnas y las columnas por filas seguirán siendo particiones, llamadas particiones conjugadas.
Así, la partición 3+2+1+1+1
Se puede convertir en 5+2+1
Esta correspondencia es biyectiva. Si en las 15 particiones consideradas ninguna podía sobrepasar la anchura de 4, sus conjugadas no podrán tener más de cuatro filas, es decir, más de cuatro sumandos.
Esto es muy interesante: Las particiones en sumandos no mayores que k coinciden en número con las particiones en no más de k sumandos.
En nuestro ejemplo: si existen 15 particiones de 8 en sumandos no mayores que 4, también serán 15 las que se obtengan con no más de cuatro sumandos libres.
Lo comprobamos, intercambiando en Cartesius el 4 con el 8, y vemos que resultan también 15:
Así que si alguna vez no puedes construir la F.G. de un tipo de particiones, puedes acudir a las conjugadas por si resulta más sencillo. El siguiente ejemplo lo aclara.
¿De cuántas formas distintas podemos descomponer el número 12 en exactamente cuatro sumandos?
Acudimos a la conjugada: Este problema es el mismo que descomponer 12 en sumas de las cuales el mayor sumando sea 4. De otra forma: debe figurar al menos un 4 y el resto ser 1,2 o 3.
De esa forma la F.G. es fácil de obtener:
(hemos suprimido el 1 en el mayor sumando)
Generalizando
Efectuamos las comprobaciones en nuestro ejemplo
Con la función generatriz y PARI
print(taylor(x^4/(1-x)/(1-x^2)/(1-x^3)/(1-x^4),x,9))
Desarrollo: x^4+x^5+2*x^6+3*x^7+5*x^8+6*x^9+9*x^10+11*x^11+15*x^12+O(x^13)
Solución: el coeficiente de 12, que es 15.
Con Cartesius
Tenemos que eliminar el cero de los sumandos, para que sean exactamente cuatro. Por eso el rango será 1..12
Resultado: 15
Problema conjugado
Ahora, en lugar de cuatro sumandos, el máximo ha de ser siempre 4, pero eso no es operativo, pues podemos eliminar siempre ese 4 y en lugar de formar una suma 12 pedimos que la suma sea 8. Este problema lo tenemos resuelto más arriba y nos resultó 15, como era de esperar.









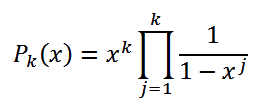


No hay comentarios:
Publicar un comentario