Según leo en el libro “Cardano y Tartaglia. Las matemáticas en el Renacimiento italiano” de Francisco M. Casalderrey, a Fibonacci le interesó mucho el estudio del triángulo de lados con medidas enteras 13, 14 y 15, porque la altura correspondiente al lado que mide 14 también tiene medida entera, 12, así como los dos segmentos que forma en la base, 5 y 9 respectivamente.
¿Existirán más triángulos con esa propiedad?La respuesta es afirmativa. Existen muchos, y no es difícil encontrarlos. Uno de ellos, con la misma superficie que el anterior, está formado por los lados 17, 21 y 10.
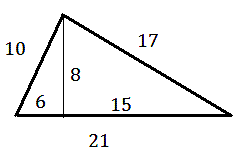¿Podrías encontrar alguno más con medidas inferiores a 50?Más difícil es que esta propiedad la presenten dos alturas. Existen algunos triángulos en los que aparece por simetría, como el de la imagen. Los lados son 25, 25 y 30, las alturas 24, 24 y 20, y los segmentos en las bases 7, 15 y 18. Todos son enteros.
¿Existirán triángulos en los que dos alturas presenten segmentos de medida entera sin acudir a la simetría? Pues también la respuesta es afirmativa. En la imagen tienes uno:
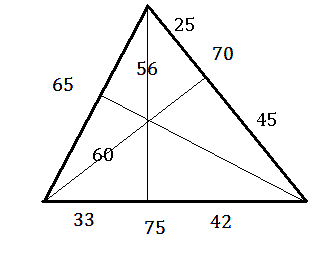Los lados miden 70, 65 y 75 respectivamente, una altura de 56 divide al 75 en dos segmentos de medidas 33 y 42, y la otra altura, de 60, divide a 70 en 25 y 45.El hecho de que este triángulo sea semejante al de Fibonacci y posea una propiedad más amplia nos demuestra que estas cuestiones no son geométricas, sino aritméticas. Todo depende de si una medida se expresa como entera o como fraccionaria. Una altura que en el primero medía 11,2. en este mide 5 veces más, lo que la convierte en entera: 56.
Con lo explicado en el párrafo anterior puedes encontrar triángulos en los que todos los lados, alturas, segmentos formados por estas en las bases, perímetro y área tengan medida entera.
Para conseguirlo puedes seguir estos pasos:
(1) Elige dos ternas pitagóricas, preferentemente primitivas, como 20, 21, 29 y 8, 15, 17.
(2) Multiplícalas ambas por un valor entero adecuado a fin de unificar las medidas de sus dos catetos mayores (el que sean los mayores no es necesario, pero te garantiza que el triángulo sea acutángulo) Puedes buscar el MCM de ambos valores. En nuestro ejemplo se convertirían en 56,105,119 y 100,105,145
(3) Arma un primer triángulo tomando como altura el cateto común:
Con esto te garantizas que el seno y el coseno de los ángulos opuestos a la altura 105 sean números racionales, y como consecuencia que también lo sean los del tercer ángulo ¿Por qué?También tienes garantizada una medida racional para las alturas y segmentos que quedan, pero no necesariamente enteros.
(4) En efecto, usando la fórmula (a2+b2-c2)/(2a) para todos los pares de lados nos resultarán las medidas de los segmentos, necesariamente racionales. Puedes verlo en un desarrollo con Wiris:
A la vista del desarrollo encontrarás los factores por los que hay que multiplicar (para conseguir una semejanza de triángulos) a fin de que todas las medidas sean enteras. En este caso por 29 y 17.
Con esto llegamos a la meta:
Sólo nos queda calcular las alturas y tendremos el triángulo completo:
Puedes analizar también el área, el perímetro y el radio de la circunferencia inscrita. Sus valores son: A= 1990571310, P=207060 y R=19227
En definitiva, de la Geometría sólo hemos usado fórmulas, por lo que el resultado constituye un regreso a la Aritmética de números enteros y racionales, que es su verdadero sitio, aunque lo hayamos representado como un triángulo. Quizás por eso le gustaba a Fibonacci.
No hay comentarios:
Publicar un comentario