En la entrada anterior iniciamos el estudio de los restos cuadráticos respecto a un módulo. Descubrimos un procedimiento algo lento para encontrar los restos y los no restos. En esta otra entrada simplificaremos algo el proceso y aprenderemos nuevos conceptos. Se aconseja leer previamente dicha entrada.
El recorrer todos los restos desde 1 hasta (p-1)/2 puede hacerse muy pesado en el caso de valores muy grandes. Euler descubrió un criterio que nos ayuda a distinguir los restos de los no restos con un solo cálculo. Es este:
Si a es un resto cuadrático respecto a p (primo e impar) se cumple
Luego, como p-1 es par, podemos escribir
De esta congruencia deducimos que uno de los paréntesis es congruente con cero, pero ambos no pueden serlo, porque entonces su diferencia, 2, cumpliría 2º0 y eso es imposible para p primo impar.
De hecho, si a es resto cuadrático, el que se cumple es el segundo, ya que si existe un x tal que x2ºa (mod p) entonces a(p-1)/2ºxp-1º1 (mod p) de nuevo por el Teorema de Fermat.
Como sólo se puede cumplir una congruencia, si a es no resto cuadrático, cumplirá la otra, con el -1.
Este criterio es bastante directo, para saber si un valor es resto cuadrático. Por ejemplo, ¿Es el 14 resto cuadrático respecto al 23?
14(23-1)/2=1411 Calculamos el resto de este último por potencias sucesivas: 141º14 (mod 23), 142º12 (mod 23) 144º12*12º6 (mod 23) 148º6*6º13 (mod 23), luego 1411º13*12*14º-1 (mod 23), luego no es resto cuadrático.
La herramienta de hoja de cálculo que proponemos, en su tercera hoja, te realiza los cálculos la aplicación de este criterio:
Es conveniente que lo intentes sin hoja de cálculo para practicar. Puedes usar la exponenciación modular (http://hojaynumeros.blogspot.com.es/2012/03/de-la-multiplicacion-rusa-la.html). La usaremos en el siguiente ejemplo:
¿Es resto cuadrático el número 70 respecto al módulo 101?
El módulo 101 es primo e impar, luego podemos usar el criterio de Euler. Bastará elevar 70 a (101-1)/2=50.
Sabemos que 50=32+16+2, luego vamos calculando: 701º-31 (mod 101), : 702º31*31º-49 (mod 101), 704º49*49º-23 (mod 101), 708º23*23º24 (mod 101), 7016º24*24º-30 (mod 101), 7032º30*30º-9 (mod 101), y ahora construimos el 50:
7050º70327016702º-9*30*49º1 (mod 101), luego según el criterio, 70 sí es resto cuadrático. Si lo compruebas con la herramienta que proponemos descubrirás que su raíz cuadrada es 26.
La aplicación de este criterio nos lleva a propiedades muy interesantes.
La primera es tan elemental que no tenemos que justificarla:
El producto de dos restos o de dos no-restos siempre da un resto, y el de resto con no resto produce un no-resto. Es decir, poseen estructura alternada, por lo que es fácil representar los restos mediante el signo + y los no restos con el -, y así poder usar la regla de los signos. Se razona fácilmente a partir del criterio de Euler.
Consecuencia inmediata:
El conjunto de restos cuadráticos forma un grupo multiplicativo en Zp
Por ejemplo, si m=11, los restos son 1, 3, 4, 5 y 9 y los no restos 2, 6,7, 8 y 10 (o bien -1, -3, -4, -5 y -9). Los restos forman un grupo, como se puede verificar fácilmente.
En la segunda hoja de la herramienta que ofrecemos dispones de una calculadora para comprobar las afirmaciones anteriores.
En particular puedes estudiar que si llamamos C al grupo de los restos cuadráticos, las clases laterales tipo a*C tienen cardinal (p-1)/2 y que por tanto el índice de C respecto a Zp es 2. Vemos una de esas clases. Multiplica el elemento 6 de Z11, por todos los elementos de C, en este caso 1, 3, 4, 5, 9: 6*1º6 (mod 11), 6*3º7 (mod 11), 6*4º2 (mod 11), 6*5º8 (mod 11), 6*9º10 (mod 11). Han resultado valores distintos, luego el cardinal de 6*C es (11-1)/2=5
Símbolo de Legendre
Esta estructura como grupo multiplicativo se expresa muy bien mediante el símbolo de Legendre (por comodidad tipográfica lo escribiremos como (m/p), con los dos números en línea, como hace Apostol).
Llamamos Símbolo de Legendre a una función que asigna a cada par de valores m y p, este último primo e impar, los siguientes valores:
(m/p)=1 si m es resto cuadrático respecto a p
(m/p)=-1 si m es no-resto cuadrático respecto a p
(m/p)=0 en el caso particular en el que m sea múltiplo de p.
En realidad, si recordamos el criterio de Euler, podemos usar una fórmula directa para encontrar el valor de un símbolo de Legendre:
Esto tiene una consecuencia práctica, y es que se pueden eliminar cuadrados al calcular el símbolo de un número compuesto.
Nótese que el valor del símbolo de Legendre es una propiedad de las clases de restos y no de los números concretos, por lo que es fácil entender que si aºb (mod p). entonces (a/p)=(b(p)
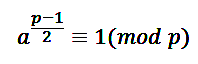
No hay comentarios:
Publicar un comentario